Текст слайда: Шар и сфера. Урок 1.
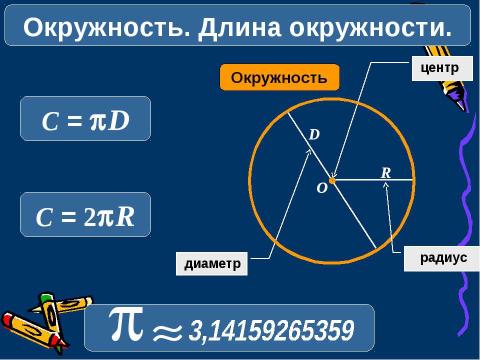
Текст слайда: диаметр Окружность Колесо центр R D O радиус p » Окружность. Длина окружности. C = pD C = 2pR
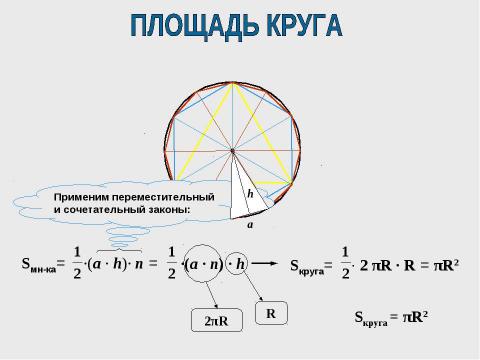
Текст слайда: ·(a · n) · h πR2 Sкруга = πR2
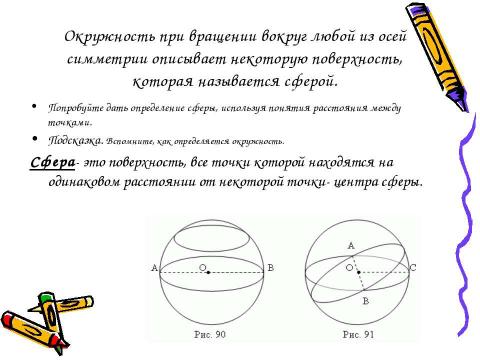
Текст слайда: Окружность при вращении вокруг любой из осей симметрии описывает некоторую поверхность, которая называется сферой. Попробуйте дать определение сферы, используя понятия расстояния между точками. Подсказка. Вспомните, как определяется окружность. Сфера- это поверхность, все точки которой находятся на одинаковом расстоянии от некоторой точки- центра сферы.
Текст слайда: По аналогии с окружностью объясните, что такое: а)радиус; б)хорда; в)диаметр сферы. Как окружность связана с кругом, так и сфера связана с шаром; Шар-это часть пространства, ограниченная сферой. У сферы и шара есть две главные формулы — формулы площади сферы и объема шара: площадь сферы Sсферы=4 R2; объем шара Vшара 4/3 R3. С выводом этих формул вы познакомитесь только в старших классах, однако это не должно мешать вам использовать их уже сейчас.
Текст слайда: S = 4πR2
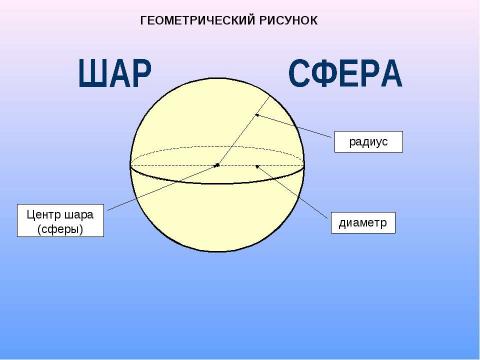
Текст слайда: диаметр радиус Центр шара (сферы) ГЕОМЕТРИЧЕСКИЙ РИСУНОК
Текст слайда: Вычислительный центр. Ребята, вы все сейчас становитесь членами вычислительного центра. От вас требуется внимательность, сосредоточенность, активность, точность.
Текст слайда: Задача 1. Найдите площадь поверхности шара радиусом 3м. Какой объем имеет такой шар?
Текст слайда: Задача 2. Найдите радиус земного шара и площадь поверхности Земли. (Радиус найдите с точностью до 100 км.)
Текст слайда: Задача 3. На рынке был куплен арбуз массой: 1)10 кг; б)16 кг. Какие примерно у него радиус и площадь поверхности? (Арбуз на 99% состоит из воды, 1 дм3 который имеет массу 1 кг) Комментарий. Арбуз практически полностью состоит из воды, поэтому можно считать, что его масса 10 кг и, следовательно, объем 10 дм3. Будем искать радиус шара объемом 10 дм3 : 10=4/3 R3≈4/3*3,14*R3 ≈4R3. Найдем R из уравнения 10=4R3; R3=2,5. Подберем значение R с точностью до 1см. R, дм 1,1 1,2 1,3 1,4 R3, дм3 1,331 1,728 2,197 2,744
Текст слайда: Из таблицы видно, что радиус арбуза больше 13см, но меньше 14см. За приближенное значение радиуса можно взять любое из этих чисел, например 13. По формуле площади сферы найдем S=4 132≈4 3,14 169 ≈2100(см2). Ответ: радиус арбуза 13 см, площадь его поверхности 2100 см2. Постарайтесь вспомнить эту задачу в конце летних каникул, когда встретитесь с арбузами
Текст слайда: Дома: §34 – формулы знать! КЗ стр.159 Творческое: Сделайте необходимые измерения предмета, имеющего форму шара, изобразите его и найдите площадь поверхности и объем.