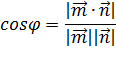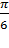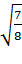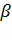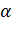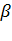Применение векторов в стереометрии, 11 класс

Этап урока

Содержание деятельности

Ожидаемый результат

Действия учителя

Действия ученика

Номер слайда презентации

1

Организация начала урока

Подготовка учащихся к работе на занятии.

Целеполагание.

Ведущий

Дорогие ребята! Приветствую вас на онлайн-уроке, по теме: «Применение векторов в стереометрии».

Вы готовы продолжить осваивать векторный метод при решении стереометрических задач?

Желаю успеха!

Полная готовность класса и оборудования, быстрое включение учащихся в деловой ритм. Обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности.

Сообщает тему урока, цель и ожидаемый результат от урока

Слушает, записывает тему урока в рабочую тетрадь.

№ 1

№ 2

№ 3

2

Актуализация опорных знаний. Осознание и осмысление учебного материала

Проверим решение домашних задач.

Задача №1.

Основанием прямой призмы АВСА₁В₁С₁ является равнобедренный треугольник АВС с основанием АВ, причем АС = 4, угол С равен 120⁰, боковое ребро АА₁ равно 8. Найдите угол между АС и ВВ_1..

Задача №2.

В правильной треугольной призме АВСА₁В₁С₁, все ребра равны 1. Найдите косинус угла между прямыми АВ и СА_1..

Вам представлены кратко записанные решения. Вы сравниваете свои решения и делаете выводы. Может кто-то из вас решил их геометрически.

Векторный метод в стереометрии заменим.

Но геометрическое решение требует дополнительных построений и подробных обоснований, что по затраченному на решение времени примерно равно, а иногда намного больше, времени на решение по алгоритму.

На прошлом уроке мы рассмотрели типы задач:

1. Угол между скрещивающимися прямыми

2. Задачи на отношение отрезков

3. Расстояние между скрещивающимися прямыми

Среди задач стереометрии, решаемых векторным методом, можно выделить две большие группы: аффинные и метрические.

В аффинных задачах выясняется взаимное расположение точек, прямых и плоскостей, а в метрических задачах находятся длины отрезков, расстояния, углы. Алгоритм их решения отличается на один пункт: составить таблицу умножения базисных векторов (только в метрических задачах).

Проверка знаний. Тест с выбором ответа из числа предложенных, из 5 заданий. На выполнение задания отводится 5мин.

Учащиеся проверяют решения по представленным ответам. Оценивают. Затем разбираются задания, вызвавшие затруднения. На доске предлагаются ответы с краткими пояснениями.

В копилку знаний.

— Что называют центроидом треугольника?

— Какой вид имеет векторное равенство для центроида треугольника?

-Что является аналогом треугольника в пространстве?

Дается определение медианы тетраэдра. Формулируется и доказывается свойство медиан тетраэдра. Дается понятие центроида и бимедианы тетраэдра. Формулируется свойство тетраэдра о том, что точка пересечения медиан и бимедиан тетраэдра совпадает.

Развитие мышления, «Я-концепции» учащихся через организацию мыследеятельности, смыслотворчества, полилога».

Установление правильности и осознанности усвоения учебного материала.

Показывает учащимся важность векторного метода и широту его применения. Предлагает классифика-цию задач по типам и алгоритм их решения. Организует работу по повторению, обобщению, систематиза-ции темы «Свойства векторов и операции над векторами».

Слушает внимательно учителя и отвечает на поставленные вопросы.

Выполняет задания, при необходимости вносит коррективы в свой конспект.

№ 4-5

№ 6-7

№ 8

№9

№10

№11

№12-№27

№28

№29

№30№31

№32

№33

№34

№35

3

Усвоение новых знаний

Вашему вниманию будут представлены Алгоритмы следующих типов задач:

• расстояние от точки до прямой;

• расстояние от точки до плоскости;

• угол между прямой и плоскостью;

• угол между двумя плоскостями.

Задача №1. Даны точки М, N и А. Найдите расстояние от точки А до прямой MN.

Задача №3. Дана плоскость α с базисом _, точка А, принадлежащая плоскости α, точка М, не лежащая в плоскости α. Найдите расстояние от точки М до плоскости α.

При нахождении расстояния от прямой до плоскости надо:

• Показать, что прямая параллельна плоскости.

• Взять произвольную точку этой прямой и найти расстояние от точки до плоскости(смотрите задачу №2).

• Полученное расстояние и есть расстояние от прямой до плоскости.

Вводится понятие угла между прямой и плоскостью, как угла между прямой и ее проекцией на плоскость, который равен углу между векторами ( направляющим вектором прямой и его вектором – проекцией на плоскость). Обращается внимание, что угол между прямой и плоскостью может быть только острым. Угол между вектором нормали (перпендикулярным к плоскостиα) и прямой m дополняет угол между прямой и плоскостью до 90˚. Поэтому для вычисления угла можно применять формулу:_.

Угол между двумя плоскостями равен

углу между перпендикулярными

к этим плоскостям прямыми.

Угол между двумя прямыми — наименьший из смежных углов,

полученных при пересечении.

Задача решается по алгоритму. Угол вычисляется по формуле: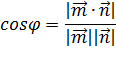

Рассмотрено выражение медианы тетраэдра через длины его ребер.

Задача № 5. Выразить длину медианы тетраэдра ABCD через длины его рёбер.

Выведенная формула записывается для другой медианы. Делается вывод.

Учащиеся умеют определять тип задачи и решают по алгоритму подобные задачи и подбирают свои. Активные действия учащихся; максимальное использование своих знаний и овладение способами действий

Представля-ет решения задач четырех типов, среди которых есть метрические и аффинные

Записывает в тетрадь задачи, осмысливает их и задает учителю вопросы

№36

№37-43

№56-60

№61

№62

№63

№74

-81

4.

Закрепление новых знаний

Задача №2. В основании прямой призмы АВСDA₁B₁C₁D₁ параллелограмм АВСD, в котором АВ = 2, АD = _ , угол ВАD равен 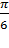_. Точка К является серединой ребра D₁C_1, расстояние от вершины B₁ до прямой СК равно 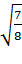_ . Найдите площадь боковой поверхности.

Задача № 4. В основании треугольной пирамиды SABC лежит правильный треугольник со стороной, равной единице, ребро SA пирамиды перпендикулярно плоскости основания, SA=_ . Плоскость α параллельна прямым SB и AC, плоскость _ параллельна прямым SC и AB. Определите угол между плоскостями _ и _.

Обеспечение усвоения новых знаний и способов действий на уровне применения.

Создание проблемной ситуации, прочтение лекции, показ демонстрационного материала с комментариями.

Сумеет применить теоретические знания для решения, предложенных учителем задач.

Выполняет задания, при необходимости вносит коррективы.

№ 44-55

№64-73

5

Рефлексия. Задание на дом.

Сегодня на уроке, мы продолжили применение векторов в стереометрии. На уроках были рассмотрены наиболее часто встречающиеся на конкурсных экзаменах задачи и алгоритмы их решения.

• Полезен ли для вас материал нашего урока?
  

• Считаете ли вы целесообразным расширение и углубление своих знаний по данной теме?
  

• Считаете ли вы необходимым индивидуально попробовать свои силы в решении задач с помощью новых методов?

Надеюсь, вы не остановитесь и продолжите самостоятельно решать задачи, и более глубоко изучите векторный метод в стереометрии. Он универсален и позволит вам сэкономить время на решение стереометрических задач.

Домашнее задание.

Задачи а) — г).

Предложенные задачи содержат очень важные утверждения, формулы, которые вам пригодятся как инструмент для решения других задач.

Удачи при выполнении домашнего задания!

Источники

Е.В. Потоскуев, Л.И.Звавич «Геометрия-10»учебник для классов с углубленным и профильным изучением математики. Москва, Дрофа 2010г.

Е.В. Потоскуев, Л.И.Звавич «Геометрия-10» задачник для классов с углубленным и профильным изучением математики. Москва, Дрофа 2009г.

Готман Э.Г., Стереометрические задачи и методы их решенияМ:МЦНМО,2006г.

Шестаков С.А.;«Векторы на экзаменах. Векторный метод в стереометрии», Москва, МЦНМО,2005г.

obr.1c.ru/product.jsp. Банк тренажеров по математике

http ://www .mahtege .ru Открытый банк заданий по математике.

Спасибо за внимание!

Осмысление учащимися изученного материала, самооценка. Обеспечение понимания цели, содержания и способов выполнения самостоятельного задания

При организации рефлексии педагог предлагает высказаться каждому участнику и задает несколько вопросов.

Делает анализ и оценку успешности достижения цели и намечает перспективу последующей работы.

Осмысливает свое состояние, высказывает замечания и вносит свои предложения.

№60-61

№82-83

№84-86

№87

№ 88

№89