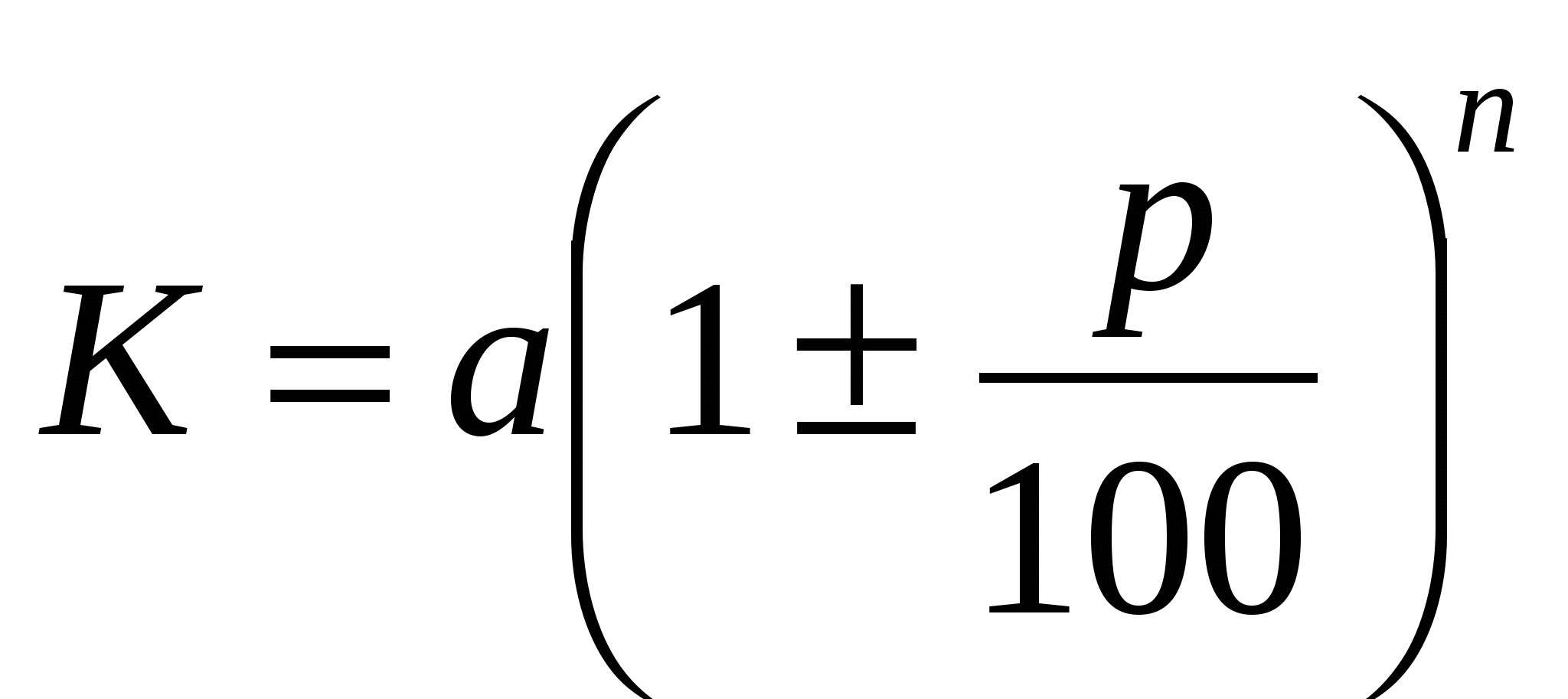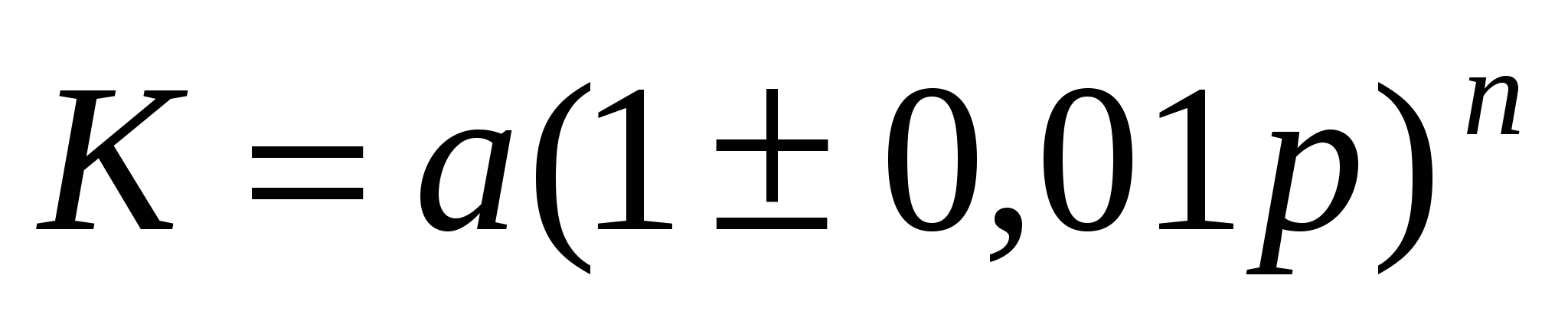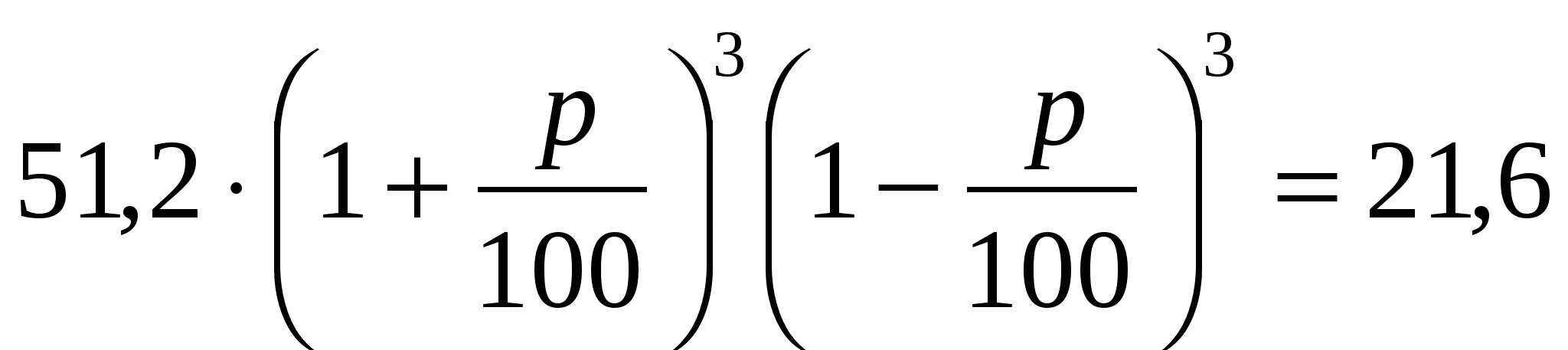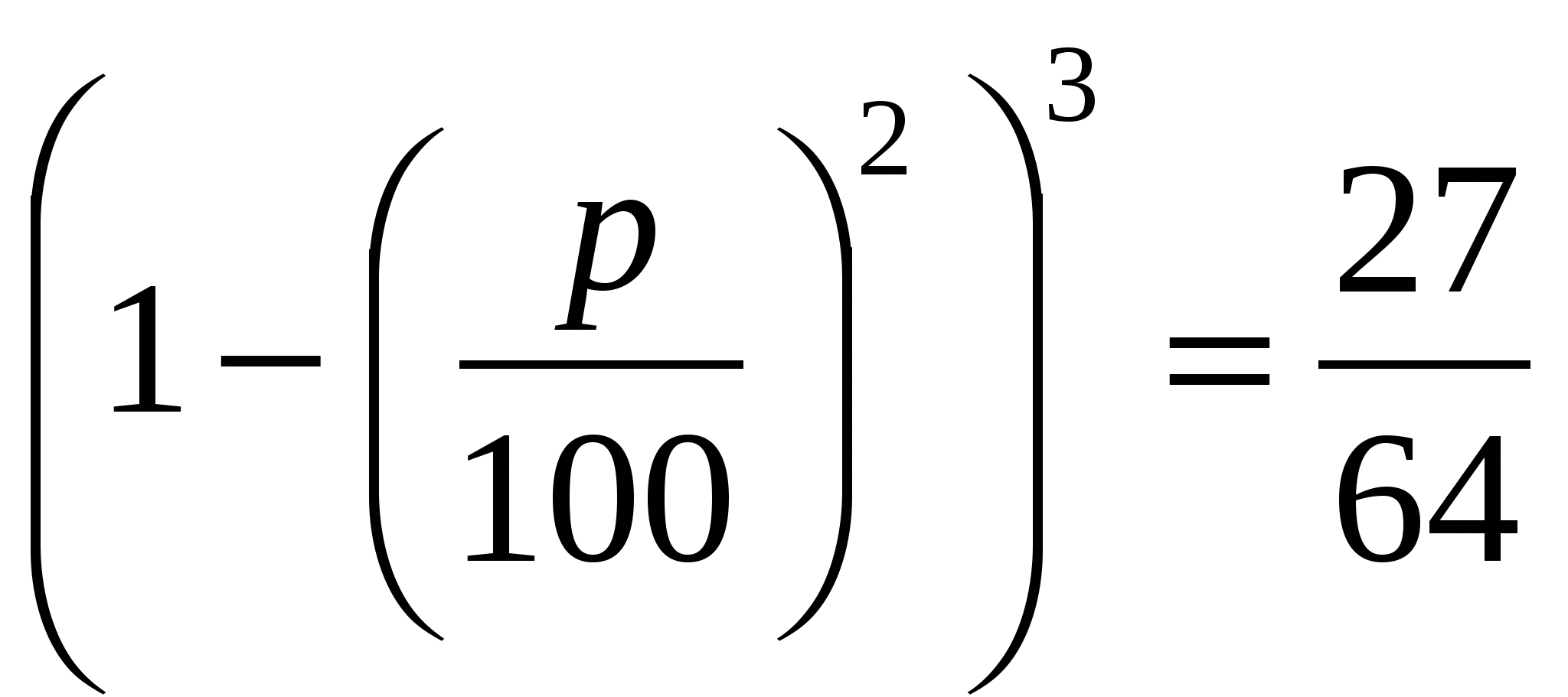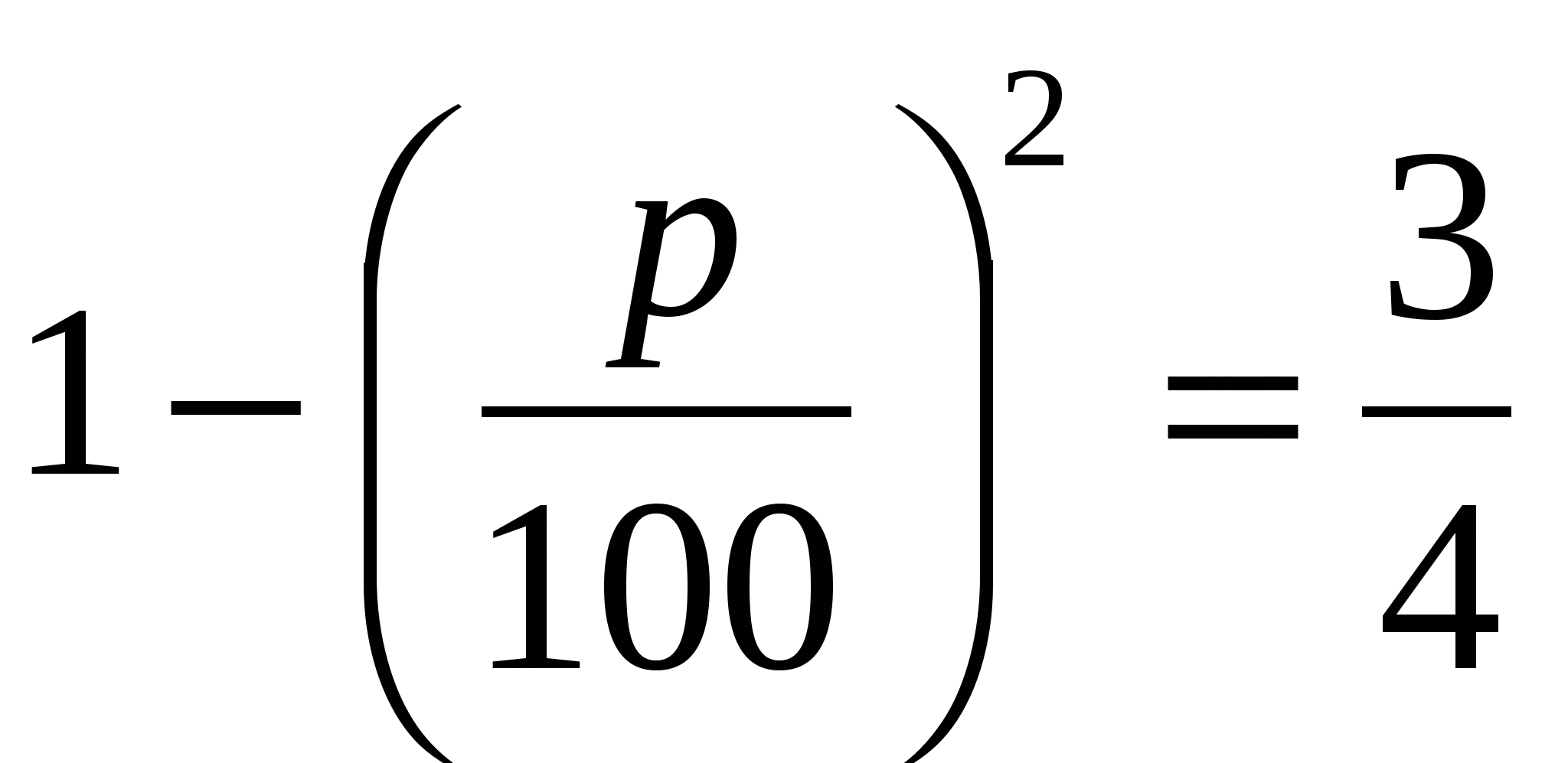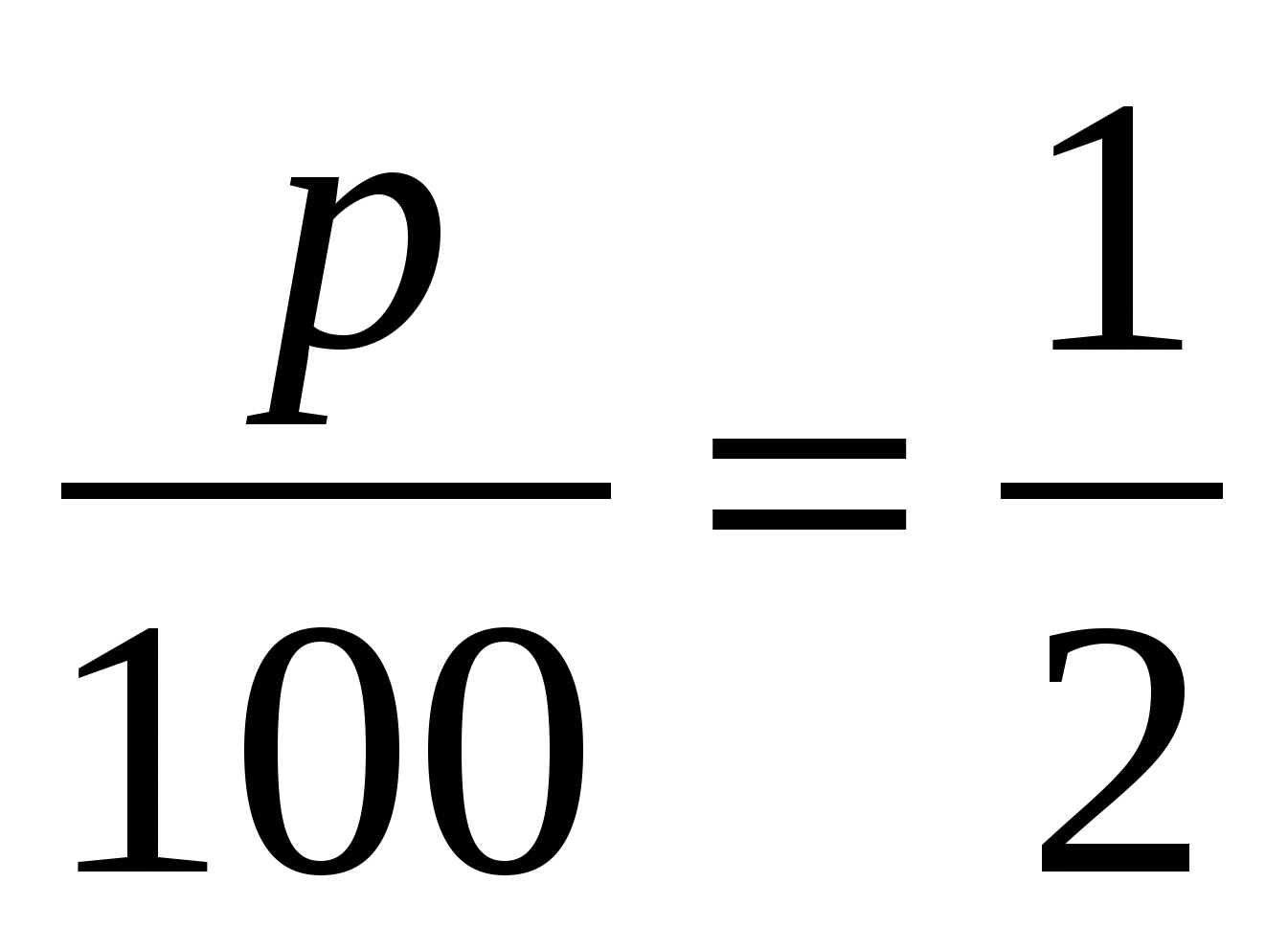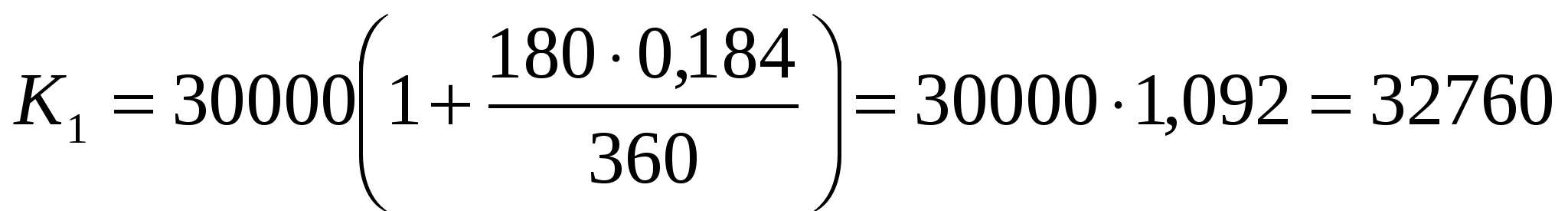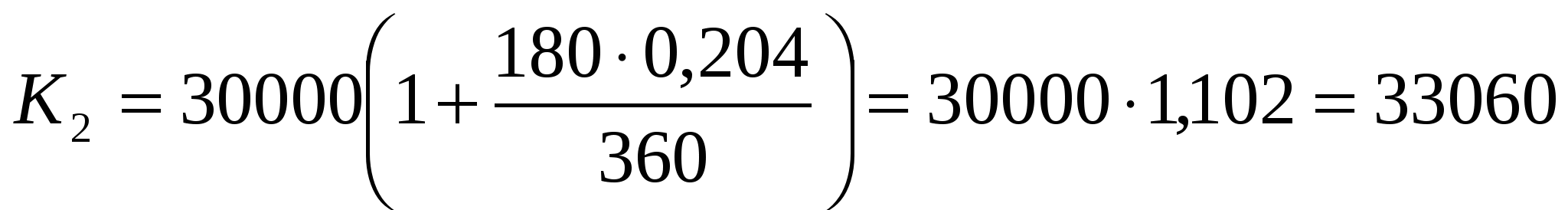Исследовательская работа «Математика в процентах и кредитах» 9 класс

МУНИЦИПАЛЬНОЕ КАЗЁННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №3»

РФ. 646020. Омская область, Исилькульский район, г. Исилькуль, ул. Советская 2а,

тел. 20 – 903, эл. адрес: schkola3_isilkul@mail.ru

Математика в процентах и кредитах.

Выполнила: Козлова Елизавета, учащаяся 9 класса.

Руководитель: Зинченко Елена Владимировна, учитель

математики и информатики

2013 г.

ОГЛАВЛЕНИЕ:

1. Введение ………………………………………………….3

2. История возникновения процента………………………5

3. Задачи на расчет сложного процента……………………6

4. Задачи на банковские проценты ………………………..9

5. Опытно-экспериментальная работа…………………….11

6. Заключение……………………………………………….13

7. Список литературы………………………………………14

Введение.

Актуальность темы:

В наше время почти во всех областях человеческой деятельности встречаются проценты. Поэтому выбранная мной тема особенно актуальна.

Без понятия «процент» нельзя обойтись ни в бухгалтерском учёте, ни в финансовом анализе, ни в статистике. Чтобы начислить зарплату работнику, нужно знать процент налоговых отчислений; чтобы открыть депозитный счёт в сбербанке, наши родители интересуются размером процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции. Именно в торговле понятие «процент» используется наиболее часто: скидки, наценки, уценки, прибыль, кредиты, налог на прибыль и т.д. – всё это проценты.

Цель данной работы:

Показать широту применения процентов и исследовать их использование при кредитовании, выяснить, какой из кредитов выгоднее.

Для достижения поставленной цели необходимо выполнить следующие задачи:

— проанализировать литературу по теме «Проценты и процентные вычисления»;

— познакомиться с формулой сложных процентов;

— показать прием полученных знаний при кредитовании (потребительский кредит).

Решение математических задач практического содержания позволяет убедиться в значении математики для различных сфер человеческой деятельности, увидеть широту возможных приложений математики, понять её роль в современной жизни.

Умение выполнять процентные расчеты необходимо каждому человеку. Поэтому сюжеты задач взяты из реальной жизни. Рассмотрены различные виды кредитования.

Ценность полученных результатов в том, что они продемонстрировали широкий спектр применения расчёта процентов в экономических сферах, то есть тесную взаимосвязь математики с экономикой.

История возникновения процента.

Слово «процент» имеет латинское происхождение: «pro centum» — это «со ста». Часто вместо слова «процент» используют это словосочетание. То есть процентом называется сотая часть числа.

Проценты были известны индийцам ещё в V в. и это очевидно, так как именно в Индии с давних пор счет велся в десятичной системе счисления.

Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню.

Римляне брали с должника лихву (т.е. деньги сверх того, что дали в долг). При этом говорили: «на каждые 100 сестерциев долга заплатить 16 сестерциев лихвы». Это можно назвать первым кредитом мира.

От римлян проценты перешли к другим народам Европы.

В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. В 1584г. он впервые опубликовал таблицу процентов.

Введение процентов было удобным для определения содержания одного вещества в другом; в процентах стали измерять количественное изменение производства товара, рост и спад цен, рост денежного дохода и т.д.

Символ  появился не сразу. Сначала писали слово «сто» так: cto.

В 1685г. в Париже была напечатана книга «Руководство по коммерческой арифметике», где по ошибке вместо cto было набрано . После этого знак  получил всеобщее признание и до сих пор мы пользуемся этим значком процента.

Задача на расчет сложного процента:

Цену 51, 2 рубля за капиллярную ручку трижды увеличивали на одно и то же число процентов, а затем трижды уменьшали на то же самое число процентов. В результате получилась цена ручки 21,6 рубля. На сколько процентов увеличили, а затем уменьшили цену капиллярной ручки?

Попробуем по приведенным числам рассчитать, на сколько процентов увеличили, а затем уменьшили цену капиллярной ручки. Это задача на расчет сложного процента. Расчет сложных процентов производится по формуле:

или ,

где а – начальное значение некоторой величины;

К— значение, которое получилось в результате нескольких изменений начальной величины;

n – количество изменений начальной величины;

р – процент изменения.

Знак «плюс» применяется в задачах при подсчете увеличения цены товара, а знак «минус» применяется при подсчете снижения цены.

Действительно, если изменение числа на р % заменить умножением на нужное число, то, увеличив число а на р%, получим .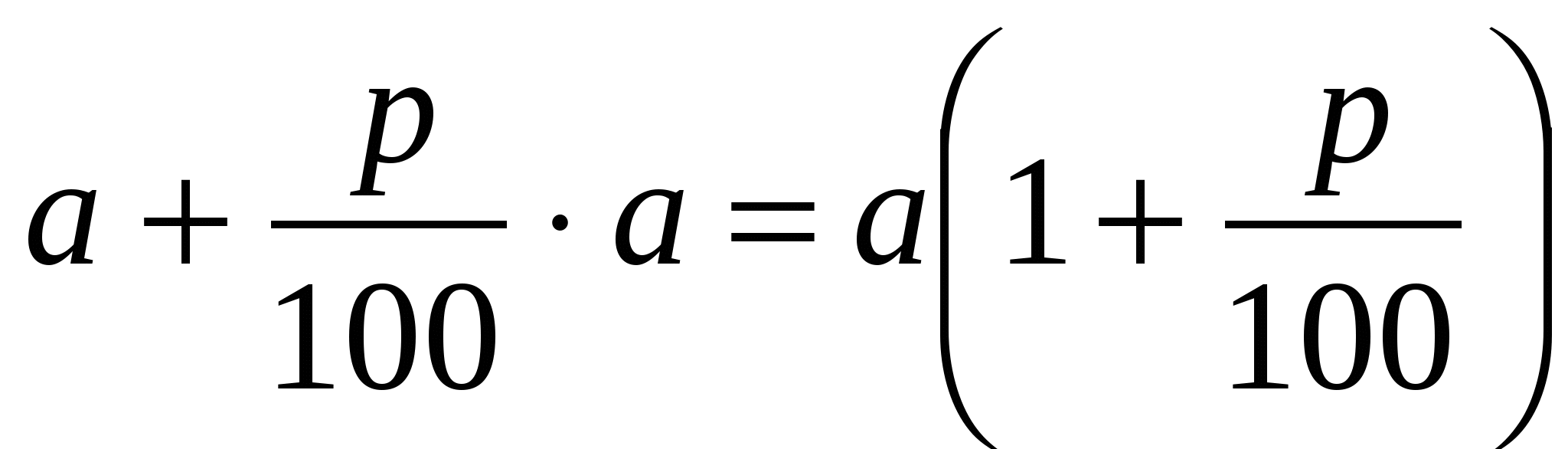

То есть чтобы увеличить число на р % , достаточно умножить его на 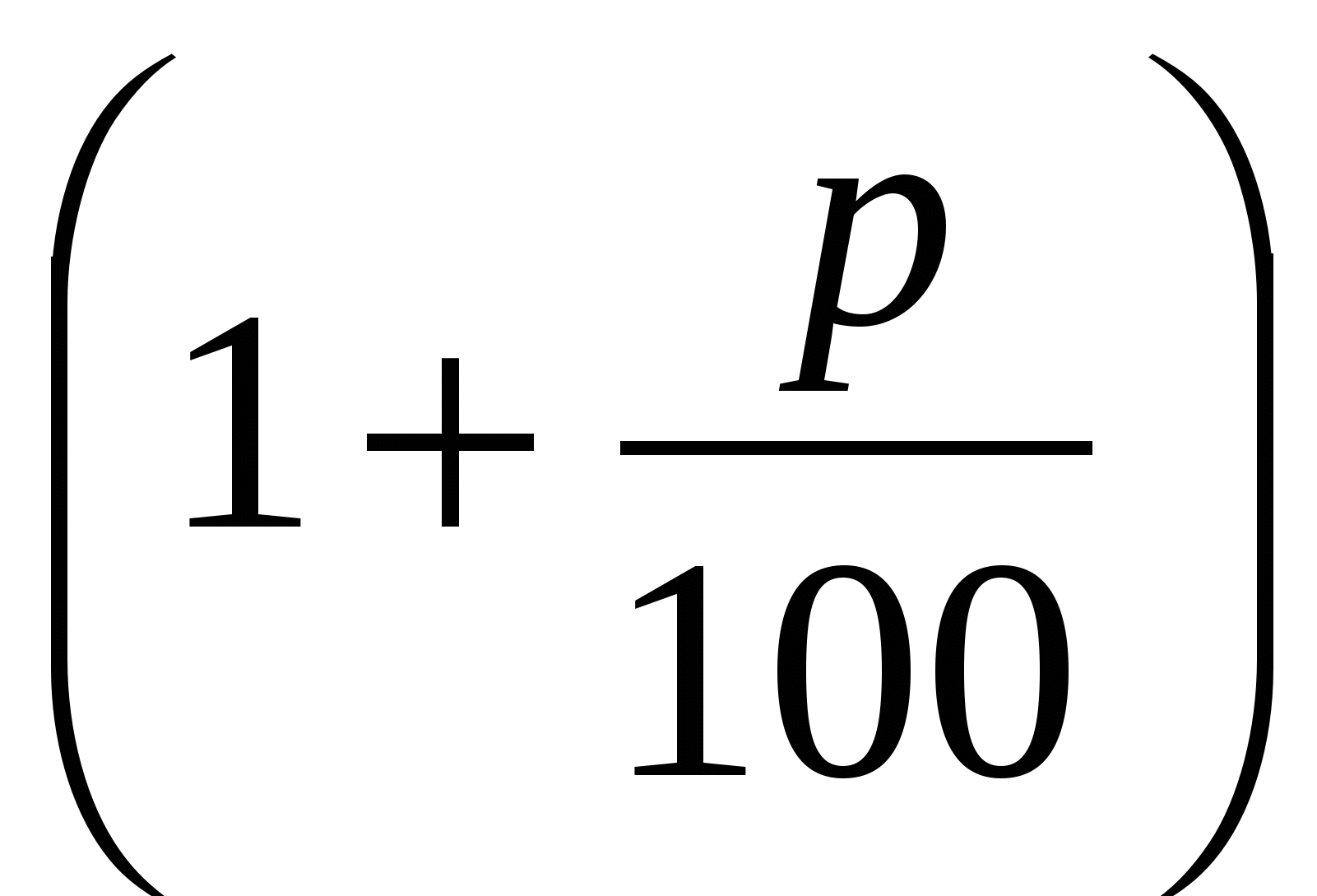, и чтобы число уменьшить на р %, достаточно умножить его на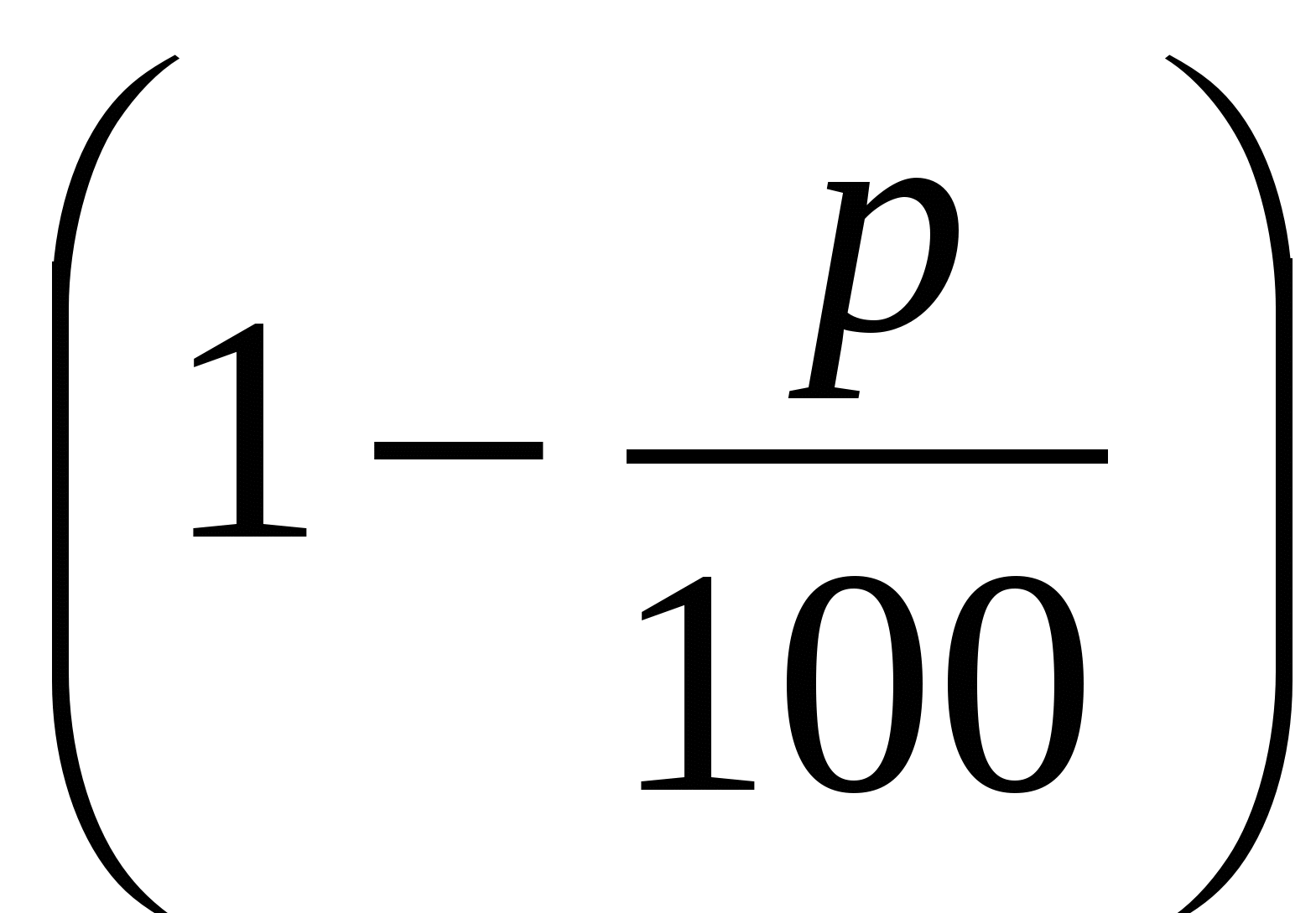

Решение: Вернемся к задаче и из условия задачи имеем

или .

;

;

;

; р=50

Ответ: цена капиллярной ручки увеличивалась и уменьшалась на 50%.

Рассмотрим ещё несколько задач на применение формулы сложного процента:

Задача 1. (из данных сберегательного банка России) вкладчик положил некоторую сумму на вклад «Молодежный» в сбербанк России. Через два года вклад достиг 2809 рублей. Каков был первоначальный вклад при 6 % годовых?

Решение:

Пусть х рублей – первоначальный вклад.

х·(1+6·0,01)²=2809

1,06² х=2809

1,1236х=2809

х=2500

Ответ: первоначальный вклад составлял 2500 рублей.

Задача 2.(из ЕГЭ) Цену на автомобиль «Волга» снизили сначала на 20%, а затем еще на 15%. При этом он стал стоить 238000 рублей. Какова первоначальная цена автомобиля?

Решение:

Пусть х рублей будет первоначальная стоимость автомобиля.

х·(1-0,2) ·(1-0,15)=238000

х·0,8·0,85=238000

х ·0,68=238000

х=350000

Ответ: 350000 рублей – первоначальная стоимость автомобиля.

Задача 3. Скорость тела, движущегося равноускоренно, каждую секунду увеличивается на 10%. В данный момент его скорость 10 м/с. Какой будет его скорость через три секунды?

Решение:

(м/с)

Ответ: через три секунды скорость будет 13,31 м/с.

Задача 4: После снижения цен на 30% свитер стал стоить 2100 рублей. Сколько стоил свитер до снижения цен?

Решения:

Воспользуемся схемами, получаем, что

S_о ∙(1-30∙0,01)=2100

S_о ∙0,7=2100;

S_о=3000

3000 (рублей) – стоил свитер до снижения цен.

Ответ: 3000 рублей.

Задачи на банковские проценты.

1. Кредит в сумме 500 000 руб. выдан на срок 5 лет под 7% годовых. Начисляются сложные проценты, периодичность начисления — в конце каждого года. Определите общую сумму задолженности по кредиту на момент погашения.

Решение.

(руб.)

Ответ: сумма задолженности на момент погашения равна 701275,87 рублей.

2. Кредит для покупки дома выдан на сумму 4 000 000 рублей сроком на 5 лет. Процентная ставка составляет 14 % годовых. Погашение кредита производится в конце каждого месяца. Определить сумму, которая должна быть выплачена за все пять лет и ежемесячный погасительный платеж.

Решение.

Эта задача решается по формуле сложных процентов с начислением процентов несколько раз в году: 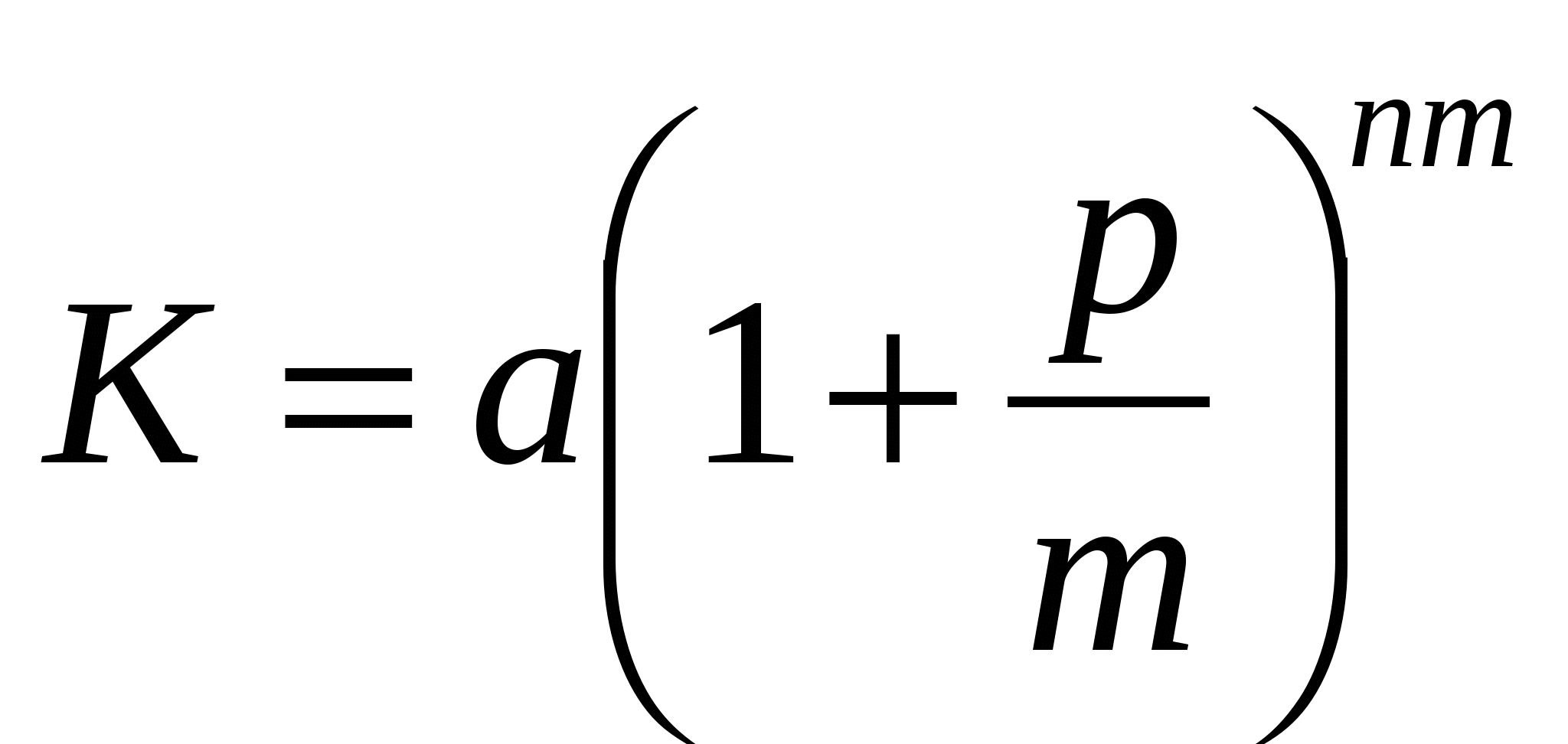( n – срок кредита, m – число выплат в год). Тогда 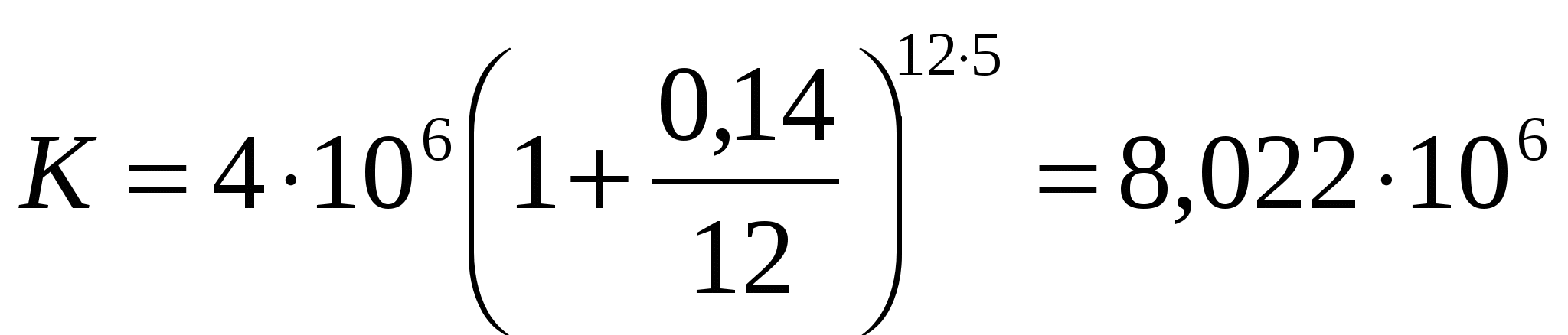(руб.) При этом ежемесячный платеж будет составлять 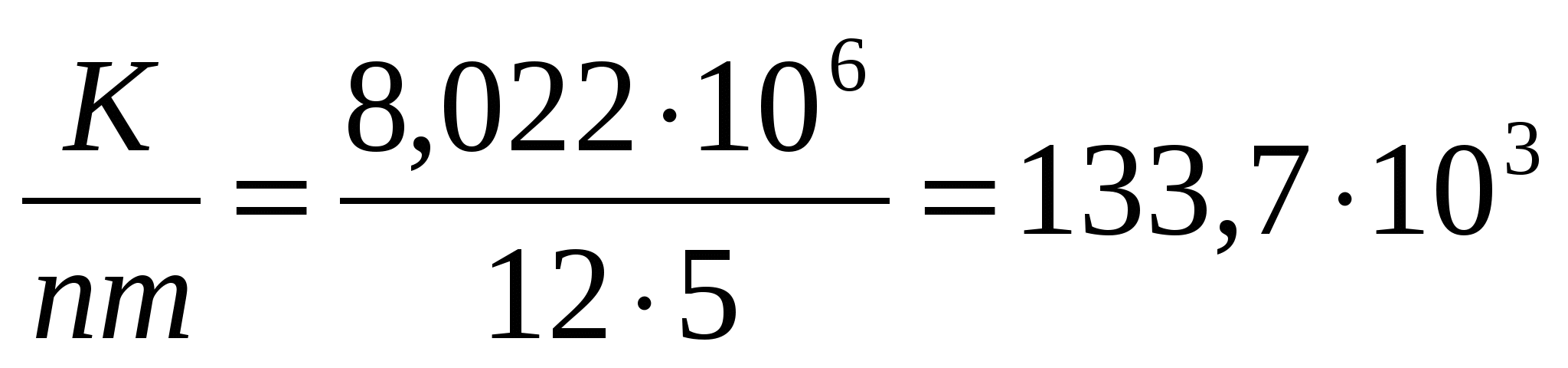(руб.).

Ответ: сумма, которая должна быть выплачена за все пять лет равна 8,02210⁶ рублей и ежемесячный погасительный платеж 133,710³ рублей.

3. Кредит в сумме 200 000 руб. выдан на срок 5 лет. Номинальная годовая ставка равна 20% годовых. Начисляются сложные проценты, периодичность начисления — в конце каждого квартала. Определите общую сумму задолженности по кредиту на момент погашения.

Решение.

, n = 5, а m = 4. (руб.)

Ответ: сумма задолженности на момент погашения 530 660 рублей.

4. 1 января вкладчик положил на счет в банке 2000 рублей по схеме обыкновенный процент и приблизительное число дней под 22% годовых. По какое число нужно делать вклад, чтобы получить 2350 рублей?

Решение.

Длительность года по схеме приблизительное, число дней будет 360. Преобразуем формулу однократных внутригодовых начислений таким образом, чтобы выделить число дней финансовой операции: 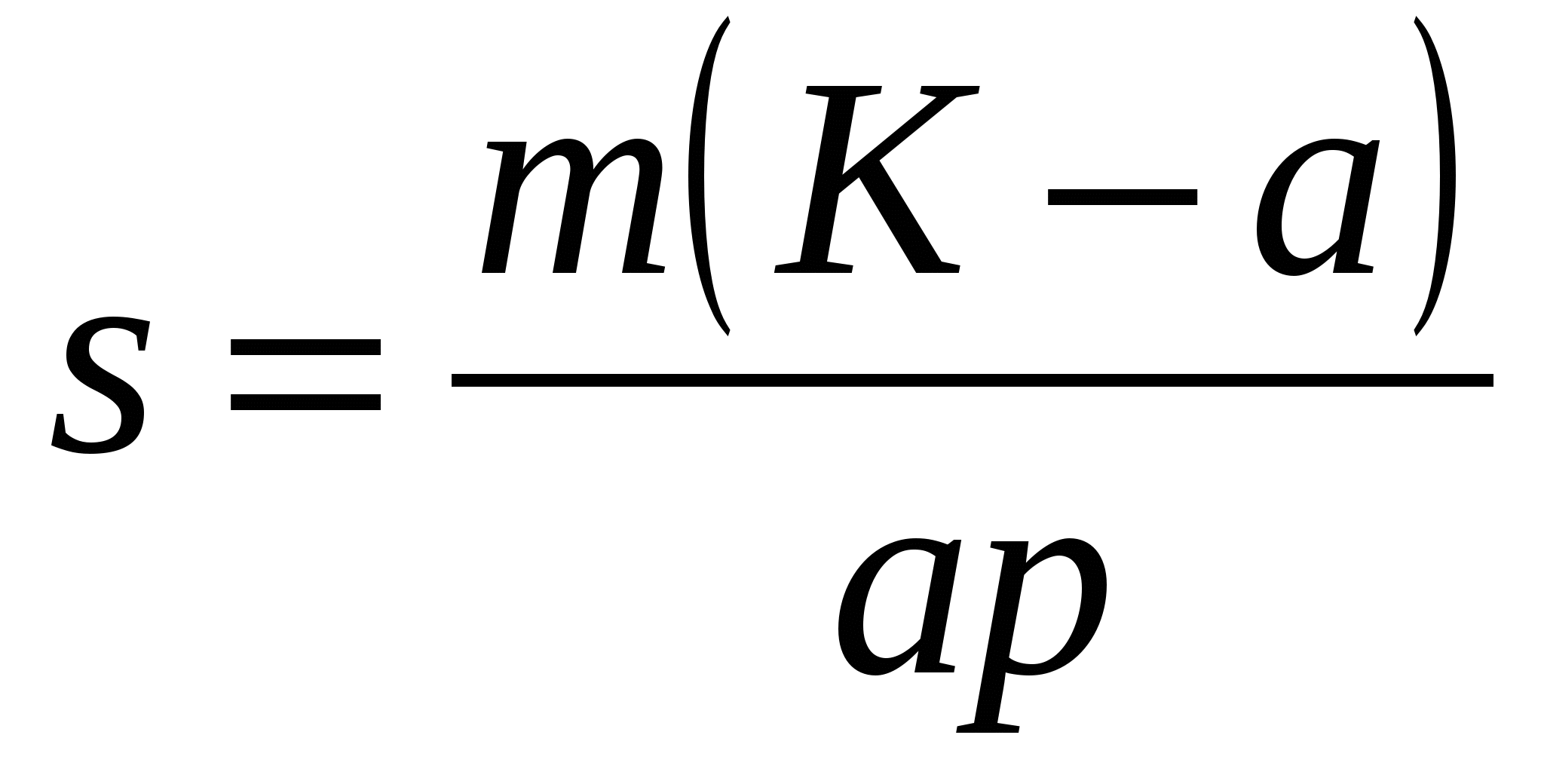; 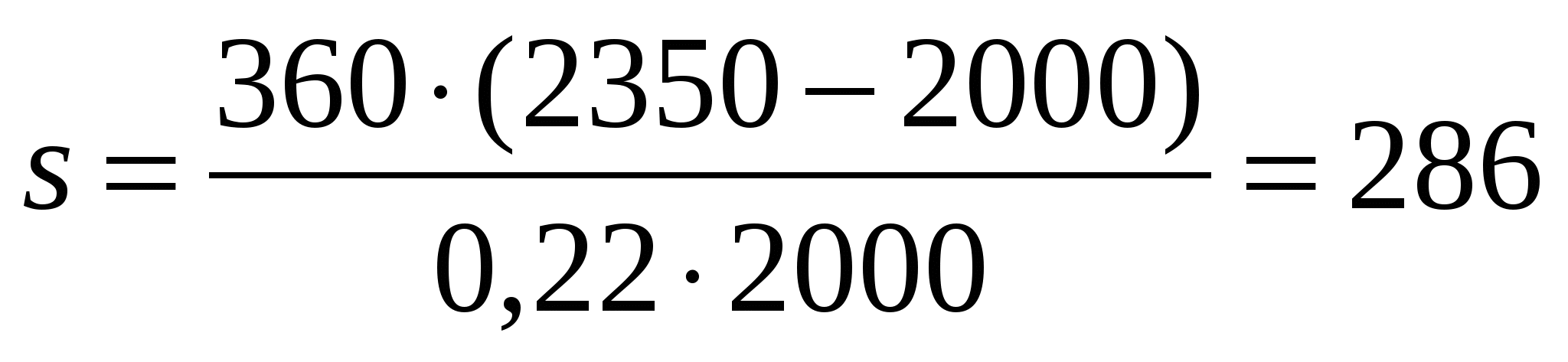(дней), т.е. 286 дней = 309 + 16 дней.
Ответ. Вклад нужно сделать на 9 месяцев и 16 дней, то есть по 16 октября.

Опытно-экспериментальная работа.

Рассмотрим практическую задачу, имеющую применение в реальной жизни – это расчет кредитов. В наше время люди все чаще и чаще берут товары в кредит (ссуда в денежной или товарной форме, предоставляемая кредитором заемщику на условиях возвратности, чаще всего с выплатой процента за пользование ссудой), который доступен каждому.

Конечно же, всем хочется приобрести нужный товар, как можно выгодней. Очень интересно, какие кредиты в нашем городе самые удобные. Для проведения этого эксперимента я рассмотрела потребительские кредиты банков, в которых учителя нашей школы получают заработную плату, «Росбанк» и «Сбербанк». Для того чтобы рассчитать итоговую сумму кредита не обойтись без формул сложных процентов.

Преобразовав формулу, получили: ,

где а – начальная стоимость кредита;

s – срок кредита;

р – годовая процентная ставка;

m — количество дней в году (360 дней, каждый месяц – 30 дней)

Предположим, нам необходимо приобрести товар на сумму 30000 рублей и рассчитаться за него в течение 6 месяцев.

Сбербанк России

Размер кредита не должен превышать Вашего дохода, умноженного на 10.

1. потребительский кредит без обеспечения (до 1 500 000 РР), ставка – 17-25,5% до 5 лет.

Рассчитаем наш кредит. 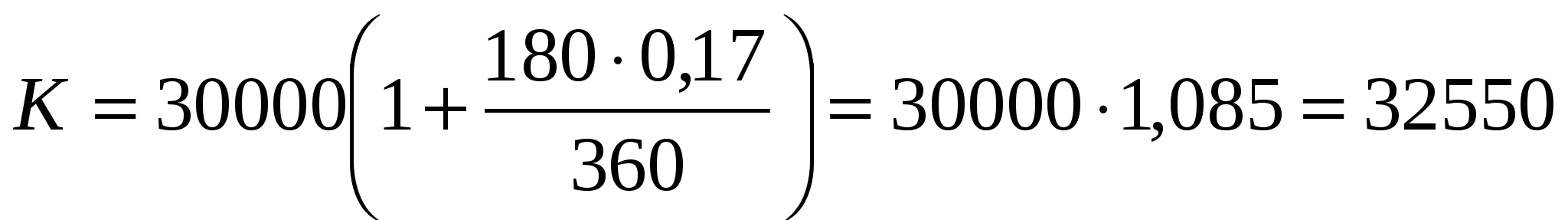рублей, т.е переплата составит 2550 рублей.

2. потребительский кредит под поручительство физических лиц (до 3 000 000 РР), ставка – 16,5 – 24,5% до 5 лет.

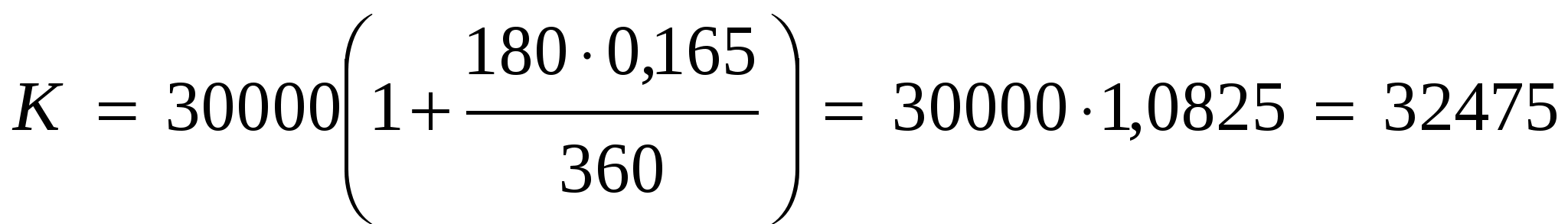рублей, т.е переплата – 2475 рублей. Этот кредит брать выгодно, но нужны надежные поручители.

Росбанк

1. потребительский кредит «Просто деньги» (от 18 000 до 40 000 РР)

Со страхованием жизни и здоровья заемщика	Без страхования жизни и здоровья заемщика
от 3 до 24 месяцев	20,4%	22,4%
от 25 до 60 месяцев	22,4%	24,4%

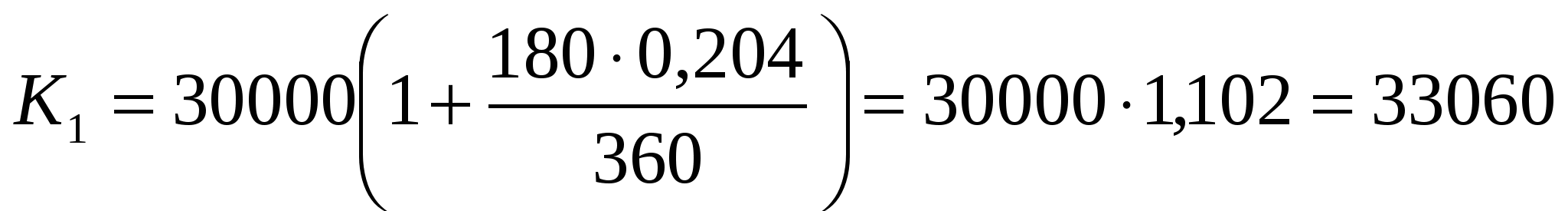рублей, переплата – 3060 рублей.

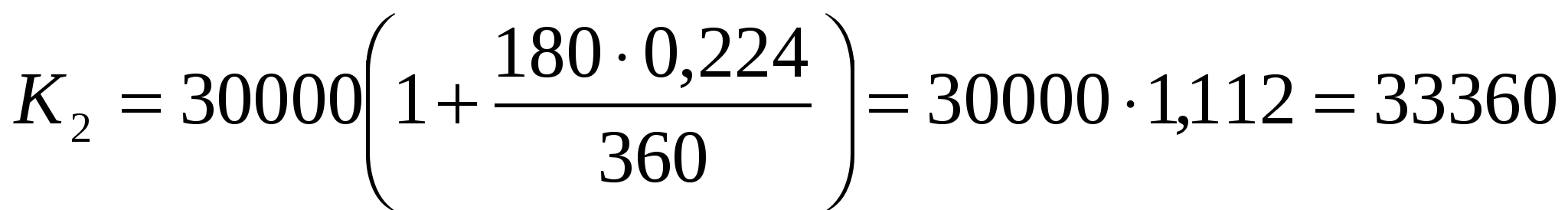рублей, переплата – 3360 рублей.

2. потребительский кредит «Большие деньги» (от 10 000 – 3 000 000 РР)

Со страхованием жизни и здоровья заемщика	Без страхования жизни и здоровья заемщика
от 3 до 36 месяцев	18,4%	20,4%
от 37 до 60 месяцев	19,4%	21,4%

рублей, переплата – 2760 руб.

рублей, переплата – 3060 руб.

Из вычислений видно, что кредит в 30 000 РР на 6 месяцев выгоднее взять в Сбербанке, а кредит на крупную сумму и длительный срок – в Росбанке. Но мы в этой работе не учитываем нюансы, которые могут быть при получении кредитов, об этом подробно расскажут в банках.

Зная формулу сложного процента, легко рассчитать выгоду кредита в любой момент. Это помогает экономить семейный бюджет.

Заключение.

В заключение хочется сказать, что умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Надеюсь, что моя работа найдет практическое применение не только на уроках алгебры и при подготовке к экзаменам, но и поможет в жизни после школы, даже если будущая профессия не будет связана с математикой.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

1. Математика. 8-9 классы: сборник элективных курсов. авт- сост. В.Н. Студенецкая.-Волгоград; Учитель, 2006. -205 с.

2. Ф.Ф. Лысенко Алгебра 9 класс. Подготовка к итоговой аттестации – 2012. – Ростов-на Дону, Легион. — 2012

3. Захарова А.Е. Несколько задач «про цены ». //журнал «Математика в школе».-2002-№8.

4. Савицкая Е.В., Серегина С.Ф. Уроки экономики в школе. – М.: Вита-Пресс, 1999.

5. http ://www .festival .1september .ru

6. http ://sberbank .ru – сайт Сбербанка России

7. http ://rosbank .ru – сайт Росбанка