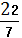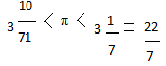Конспект урока по Математике «Урок–игра по математике «Путешествие в Древнюю Грецию» 6 класс

Путешествие в Древнюю Грецию

Урок–игра по математике

6-й класс

Пасичник Юлия Анатольевна, учитель математики МБОУ г. Мурманска СОШ № 38

Тип урока: урок первичного предъявления новых знаний.

Форма проведения урока: проблемный урок.

Методы: проблемно-поисковый.

Цель урока:

Образовательные:

• познакомить учащихся с формулой длины окружности;

• познакомить с историей возникновения математических понятий по теме «Длина окружности»;

• приобретение навыков исследовательской работы;

• закреплять умения и навыки использования формул для вычисления длины окружности.

Развивающие:

• развивать математическую речь, память, умение анализировать, обобщать и делать выводы;

• развивать познавательный интерес к предмету, логическое мышление, пространственное воображение; 

• развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;

Воспитательные:

• воспитывать прилежание, аккуратность, трудолюбие, чувство коллективизма, умение слушать и слышать;

• воспитывать уважение и интерес к математике, умение видеть математические задачи в окружающем нас мире;

Здоровьесберегающие:

• способствовать сохранению и укреплению здоровья учащихся через физкультминутку.

Идея урока. Данный урок математики является уроком новой темы «Длина окружности». На уроке учащиеся развивают умение наблюдать, анализировать, участвовать в диалоге друг с другом, делать выводы, оценивать свои действия. Формулы выводятся учащимися в результате практической работы по измерению длины окружности и площади круга. Презентация позволяет дать больший по объёму материал, поддерживать у учащихся интерес к изучаемому материалу.

Обеспечение урока. ПК, экран, проектор, колонки, презентация Power Point; полоски из картона, линейки, модели окружности, циркуль для демонстрации.

План урока.

1. Этап 1: Орг. момент – 1 мин.

2. Этап 2: Подготовка учащихся к усвоению знаний – 4 мин.

• устное выполнение заданий.

3. Этап 3: Приобретение новых знаний – 15 мин.

• создание проблемной ситуации;

• практическая работа;

• формулирование вывода;

• вывод формул;

• историческая справка.

4. Физкультминутка. – 1 мин.

5. Этап 4: Закрепление новых знаний – 15 мин.

6. Этап 5: Анализ и обобщение – 5 мин.

• подведение итогов;

• рефлексия;

• домашнее задание;

• оценки за урок.

Ход урока:

Этап 1: Орг. момент – 1 мин.

Приветствие учащихся. Вступление.

Здравствуйте, ребята! Позвольте представиться, меня зовут Пасичник Юлия Анатольевна, я учитель математики школы №38. Давайте настроимся сегодня на позитивную и продуктивную работу!

Для того чтобы нам сегодня было удобно работать, у каждого на парте лежит опорный конспект.

А тему нашего занятия мы узнаем в конце урока.

Этап 2: Подготовка учащихся к усвоению знаний – 4 мин.

Посмотрите, пожалуйста, на экран и скажите, из каких геометрических фигур получились эти предметы? (Слайд)

( круг, окружность)

Чем отличается круг от окружности?

(Окружность — это замкнутая линия, все точки которой одинаково удалены от центра.

Область внутри окружности вместе с окружностью называется кругом.)

Открываю надписи на плакатах окружность и круг

Свои названия окружность и круг получили в Древней Греции.

Окружность с греч. perimetron (περιφέρεια) – периметрон, которое и означает «окружность»

Круг – «циркулус» — латинское слово.

Окружность – удивительно гармоничная фигура, древние греки считали её самой совершенной, так как окружность – единственная кривая, которая может “ скользить сама по себе”, вращаясь вокруг центра. (Слайд)

1. Заполните пропуски у себя в конспекте:

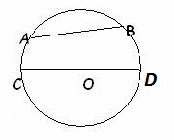
отрезок АВ – это…. (хорда) А какой отрезок называют хордой?

отрезок СD – это…. (диаметр) А какой отрезок называют диаметром? d

отрезок ОD – это…. (радиус) А какой отрезок называют радиусом? r

(Отрезок, соединяющий две точки окружности, называется ее хордой.

Отрезок, соединяющий две точки окружности и проходящий через центр окружности, называется ее диаметром.

Отрезок, соединяющий центр окружности и любую точку окружности называется радиусом.)

(открываю плакат со словами радиус, диаметр, хорда)

Кстати «хорда» (от греч. «хорде») – струна.

Раньше радиусом (от лат. radius ) называли спицу в колесе, а диаметр (с греч. διάμετρος) поперечником.

Как связан диаметр с радиусом?

( Диаметр содержит в себе два радиуса. d = 2r; r = d:2 )

( открываю формулы на плакате ) (Слайд)

Какой инструмент мы используем, чтобы построить окружность? (Циркуль!)

(показываю инструмент). Кстати слово циркуль произошло от слова круг – циркулус.

Этап 3: Приобретение новых знаний – 15 мин.

Как можно найти длину диаметра или радиуса? (измерить линейкой).

Измерьте длину окружности линейкой. (проблема: нельзя измерить)

А как вы думаете, что мы с вами сегодня на уроке научимся делать?

(измерять длину окружности)

Правильно! А чтобы узнать, как измерить окружность мы отправимся в Древнюю Грецию! А как вы думаете почему именно туда?

А как нам попасть в Древнюю Грецию из 21 века? (на машине времени)

Правильно, нужна машина времени!

Но, чтобы ее запустить нам придется ввести секретный код!

2. Верно или неверно:

а) 32,846 до десятых ≈ 32,9 (нет) П в) 1,7535 до тысячных ≈ 1,754 (да) С

б) 32,050 до целых ≈ 33 (нет) У г) 1,079 до сотых ≈ 1,08 (да) К

(после правильного выполнения каждого примера появляются буквы ПУСК)

Ура! Машина запущена! (Слайд)

(звучит музыка, заставка на экране или кадр из мультика; тем временем я надеваю накидку и лавровый венок ) (Слайд)

И мы с вами попали в город Сиракузы в III в.до н.э. и поучимся сегодня в древнегреческой школе.

Добро пожаловать в школу Архимеда! – «хайрате, пайдес!», что в переводе означает, здравствуйте, дети!

Меня зовут меня Юлиус Анатолиус и сегодня я ваш учитель (от греч.) — «сопровождающий» .

Будьте усердны, бойтесь наказания. Приходите сюда, едва поднимется солнце, и уходите не раньше первых сумерек. Вы начинаете учиться, и весь ваш город с надеждой смотрит на будущих горожан, ожидая, что вы вырастите опорой Родины и приумножите ее славу и богатства.

Сегодня у вас по расписанию:

Занятие №1 «πείραμα» (по греч. опыт)

На каждую парту розданы модели окружности (для каждого ряда разный диаметр модели), картонная полоска, линейка. Задача каждой пары выполнить практическую работу и заполнить таблицу на бланке, (номер опыта – это номер ряда); для этого нужно: выполнить все по плану, изложенному в бланке.

Сегодня мы будем ставить опыт.

У вас на партах модели окружности, картонная полоска, линейка.

Как вы думаете, зачем нам нужна полоска картона?

(чтобы было удобно измерить длину окружность) показываю.

Работать мы будем в парах.

Определите, кто из вас в паре будет измерять длину окружности, а кто записывать. Следите за тем, не делает ли напарник ошибок, если делает, то тактично и доброжелательно исправляйте его. Помните, что в любом коллективном деле нужна согласованность действий и готовность помочь своему товарищу.

В ваших опорных конспектах написан план работы. Каждый ряд заполняет только одну колонку с номером опыта: 1 ряд – опыт 1, и т.д.

Цель работы: найти отношение С к d.

План практической работы:

1. Возьмите полоску картона и с её помощью измерьте длину окружности модели (С);

2. С помощью линейки измерьте полученную длину на полоске картона;

3. Запишите результат в таблицу (С);

4. Измерьте диаметр окружности модели (d) с помощью линейки;

5. Запишите результат в таблицу (d);

6. Найдите отношение С к d (С:d);

7. Округлите результат до сотых;

6. Запишите результат в таблицу.

Работа в парах.

На доске: (то же и на бланках)

Обозначение	Опыт №1	Опыт №2	Опыт №3
Длина окружности, мм	С
Диаметр, мм	d
Отношение длины окруж-ти к диаметру	C:d

А теперь один представитель от ряда запишет свои результаты на доске в таблицу.

Заполните оставшиеся колонки с результатами ваших одноклассников.

Посмотрите на все три результата. Что вы заметили? (Какими бы различными ни были окружности, отношения их длин к диаметрам будут постоянно одинаковыми. С больше d приблизительно в 3 раза.)

Вы сделали правильный вывод. (Слайд) Вопрос о вычислении отношения длины окружности к диаметру, то есть числа π — первой буквой от греч. слова окружность — «пи», занимал лучшие умы человечества на протяжении тысячелетий. Первые вычисления π было предпринято величайшим математиком древности Архимедом. Он доказал, что

Запишите в конспект чему равно π =≈ 3,14.

Всю жизнь ученые предпринимали неудачные попытки окончательно найти значение π. Пока рекорд принадлежит японскому математику Ясума Канада. В 2004 году он рассчитал число π на компьютере до 1,24 триллиона знаков.

А знаете ли вы что, 14 марта будет отмечаться День пи – неформальный праздник математиков. «Отцом» этого праздника стал физик Лари Шоу из Сан Франциско, в 1987году, обративший внимание на то, что этот день приходится на 3,14 в американской системе записи дат. А в Сиэтле установлена металлическая скульптура числа π. (Слайд)

Вернемся к нашей проблеме нахождения длины окружности. А сможете ли с помощью всё той же картонной полоски найти длину любой окружности.

Конечно же нет, но зная, что π = С:d.

Как из этого выражения найти чему равна длина окружности С?

(С = π *d)

Обратите внимание как пишется эта буква!

Как прописная буква п, но маленького размера π.

Я могу записать эту формулу, используя обозначение радиуса?

(А как можно представить с помощью радиуса?) ( да, так как d= 2r , заменить, то можно подставить эту формулу в нашу формулу )

С = 2* π *r (Слайд)

Запишите эти формулы на свой бланк.

(Попросить учеников прочитать эти формулы и сказать что такое С, r и d)

Физкультминутка. – 1 мин.

А теперь Перемена

Встаньте ровно.

Повторяйте за мной движения и внимательно слушайте стихотворение, потому что потом придется ответить на мой вопрос.

Чтобы нам не ошибаться,

Надо правильно прочесть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Ну и дальше надо знать,

Если мы вас спросим —

Это будет пять, три, пять,

Восемь, девять, восемь.

Спасибо, садитесь. А кто мне скажет, что за числа я читала в стихотворении?

(это число пи)

Зачем нужно π, да еще с такой точностью?

(Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π). Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку.

Этап 4: Закрепление новых знаний – 15 мин.

А теперь Занятие №2 εμπειρία (с греч. практика)

У вас на партах лежат карточки с задачами. Положите их перед собой так, чтобы вам было удобно работать.

1) На клеточной бумаге изображена окружность, найдите длину окружности, если известен радиус. (π≈3) Считать, что 1 клетка = 1см.

(обсудить решение, записать его в конспект, 1 ученик у доски)

Дано: r = 4см, π≈3

Найти: С

С = 2 πr = 2 3 4 = 24 (см)

Ответ запишите в тетради. (Слайд)

(далее решаем задачи, обсудить решение, записать его в конспект, 1 ученик у доски)

Ценнейшее дерево Греции – платан, оно может достигать до 50 метров в высоту и до 20 метров в диаметре. Какой длины должна быть ограда из сетки, чтобы охранять это дерево от браконьеров? (π≈3,14)

(Слайд)

Бегун Агамненон готовиться к олимпийским играм и ему нужно узнать длину марафонской дистанции, которую нужно пробежать. Известно, что дистанция круговая и что судья, проходит из центра до края дистанции расстояние 7 км. (π ≈ 3) (Слайд)

( Запасные задачи:

В древней Греции самым важным оружием был щит, причем был он круглой формы и немного выпуклым. Щиты делали из деревянных пластин и обтягивали кожей.

Военачальник Демосфен поставил перед своим оружейником задачу: оббить полоску серебра по краю щита с надписью «Счастливой судьбы!». Какой длины должна быть серебряная полоска, чтобы хватило на обивку щита и без излишков, если щит был диаметром 80 см? (π ≈ 3,1) (Слайд)

Театр греков —древнейший на территории Европы. Орхестра (др.-греч.  ὀρχήστρα) в античном театре — круглая площадка для выступлений театральных актёров, хора или музыкантов. Какой длины должна быть изгородь, которая отгораживает зрителей от актеров, если орхестра радиусом 15м. (π ≈ 3,14) (Слайд) )

Ребята, нам пора возвращаться! Нельзя нарушать временной ход, а в греческой школе сейчас начнется урок музыки и поэзии. Ой! Что такое? Машина наша не заводится! (издается звук не заводящегося мотора машины). Но мы ее сможем завести, если ответим на вопрос от священного животного Древней Греции!

Устно: Какое расстояние проедет кошка на колесе, диаметр которого 4 дм, за 2 оборота? (π ≈ 3) (24дм) (слайд) (изображение кошки с ответом, звук заводящегося мотора)

«Хайрете!» -до свидания! «Келой кай агатой» — прекрасные и совершенные!

(Отворачиваюсь, выхожу из образа)

Ну вот мы и в 2013 году в г. Мурманске.

Этап 5: Анализ и обобщение – 5 мин.

Скажите, а какая же тема была нашего урока? (Длина окружности)

Запишите тему у себя в конспекте. С помощью каких формул можно найти длину окружности? (вспоминают формулы)

Рефлексия.

А теперь посмотрите на экран выберите фразу и продолжите её, можно продолжить несколько фраз (дети по желанию отвечают по очереди)

1. сегодня я узнал…

2. было интересно…

3. я понял, что теперь я смогу…

4. я научился…

5. знания, полученные на уроке …

6. меня удивило…

7. мне захотелось…

Дома: Всемирно известная компания Microsoft давно пользуется следующим вопросом при тестировании специалистов, которых собираются брать на работу: «Как вы думаете, а почему канализационные люки делают круглыми, а не квадратными?» Представьте, что вы сотрудник, устраивающийся на работу в эту компанию. Как бы вы ответили на поставленный вопрос? Рассчитайте длину окружности люка, если его диаметр равен 860мм ( π ≈ 3,1).

Дополнительная задача: Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1 метр, то сможет ли между проволокой и землёй проскочить мышь?

Спасибо за урок! Сегодня за урок я поставлю оценки…Приятного вам дальнейшего дня.