Викторина по математике для учащихся 6 класса

МКОУ Бадажковской ООШ, учитель математики Кудряшова Т.И.

Викторина по математике для учащихся 6 класса

по дополнительному материалу из учебника математики для 6 класса авторов Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда

1. Какое число называются совершенными?

2. Чем отличаются простые числа от составных чисел?

3. Что представляет собой «решето Эратосфена»?

4. Какие числа древнегреческие и древнеиндийские математики называли фигурными?

5. Какими геометрическими фигурами являются боковые грани и основание пирамиды?

6. От чего зависит название пирамид?

7. Чем отличается треугольная пирамида от прямой треугольной призмы?

8. Где появилась запись дробей с помощью числителя и знаменателя и чем она отличается от современной записи обыкновенных дробей?

9. Что означает слово «пропорция» от латинского «proportio»?

10. Что обозначало понятие «золотое сечение» для математиков древности и средневековья?

11. Где чаще всего применяется золотое сечение?

12. Кто из математиков предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую?

13. Как велико было число, которое мог назвать величайший древнегреческий математик и физик Архимед?

14. Какого древнегреческого математика считают «отцом алгебры» и почему?

15. Кто из великих математиков первым начал использовать слова «абсцисса», «ордината», «координаты»?

Ответы к викторине по математике для учащихся 6 класса

1. Число, равное сумме всех его делителей (без самого числа), называют совершенным числом. Например: 6=1+2+3, 28=1+2+4+7+14

2. Простые числа имеют только два делителя (1 и само число), а составное число имеет больше двух делителей.

3. Для отыскивания простых чисел греческий математик Эратосфен придумал способ вычеркивания из списка чисел (по порядку) составных чисел. Греки делали записи на покрытых воском табличках или натянутом папирусе, а числа не вычеркивались, а выкалывались иглой, а таблица в конце вычислений напоминала решето. Поэтому метод Эратосфена называют решетом Эратосфена.

4. Древнегреческие и древнеиндийские математики называли фигурными числа, которые соответствовали количеству точек, расположенных в виде некоторой геометрической фигуры – треугольника, квадрата и др. ( Число 10 называли треугольным, число 16-квадратным и т.д.)

5. У пирамид боковые грани – треугольники, а основание – многоугольник.

6. Название пирамид зависит от того, какой многоугольник является её основанием. Если основание пирамиды треугольник- то пирамида называется треугольной, если – четырехугольник , то пирамида называется четырехугольной и т.д.

7. У прямой треугольной призмы боковыми гранями являются прямоугольники, а у треугольной пирамиды – треугольники.

8. Запись дробей с помощью числителя и знаменателя появилась в Древней Греции, только греки знаменатель записывали сверху, а числитель – снизу.

9. Слово «пропорция» (от латинского proportio) означает «соразмерность», определенное соотношение частей между собой»

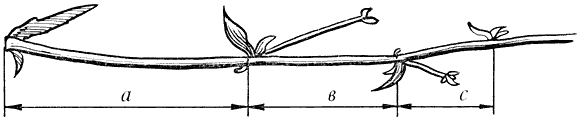
10. Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина его большей части так относится к длине отрезка, как длина меньшей части к большей. Это отношение приближенно равно 0, 618 =

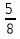
11. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается в природе.

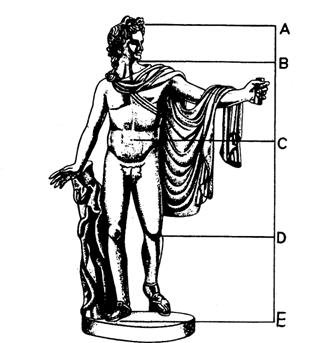
Аполлон Бельведерский Парфенон

Аполлон считается образцом мужской красоты.

Парфенон – это одно из красивейших произведений древнегреческой архитектуры

Цикорий

Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

12. Французский математик, физик и философ Рене Декарт предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую?

13. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилось бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.

14. Древнегреческого математика Диофанта считают «отцом алгебры», потому что он внес большой вклад в создание алгебры, умел решать очень сложные уравнения, применял для неизвестных буквенные значения, ввел специальный символ для вычитания, использовал сокращения слов

15. Слова «абсцисса», «ордината», «координаты» первым начал использовать в конце XVII века Готфрид Вильгельм Лейбниц.

Литература

1. Архимед. Исчисление песчинок (Псаммит). — М.-Л., 1932.

2. Учебник Математика. Учеб. для общеобразоват. учреждений/ Н.Я. Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. — М.: Мнемозина, 2011.

3. Учебник-собеседник Математика для 5-6 классов. Л.Н.Шеврин, А.Г. Гейн и др.

4. Интернет ресурсы:

• Единая коллекция цифровых образовательных ресурсов для системы общего и начального профессионального образования: http://school-collection.edu.ru

• Википедия. Свободная энциклопедия. ru.wikipedia.org›Решето Эратосфена

• Псаммит -Википедия. ru.wikipedia.org›Псаммит

• Википедия. ru.wikipedia.org ›Категория: Древнегреческие   математики