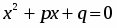
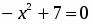
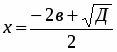
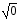
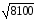
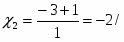
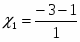
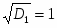
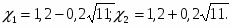
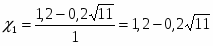
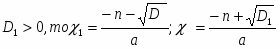
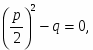
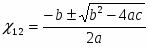
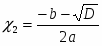
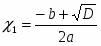
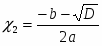
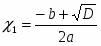
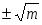
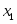
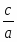
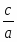
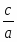
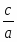
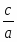
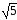
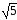
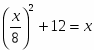
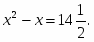
ГОУ СПО «Кунгурское педагогическое училище»

Формирование умения решения квадратных уравнений в 8 классе

Курсовая работа

по методике математики

Исламовой Энзиры

Таузифовны

Специальность: 050201

Математика

группа: М — 41

отделение: очное

руководитель:

Янкина Л.Г.

преподаватель

математики

Защита состоялась:

Отметка:

2007

Содержание

Введение 3

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1. Из истории возникновения квадратных уравнений 6

2. Основные направления изучения линий уравнений в школьном курсе алгебры 12

3. Методика изучения квадратных уравнений 15

Глава 2. Методико-педагогические основы обучения решению квадратных уравнений

1. Урок – лекция по теме «Формула корней квадратного уравнения с четным вторым коэффициентом» 23

2. Урок – практикум по теме «Квадратные уравнения» 28

3. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» 32

Заключение 37

Список литературы 38

Приложение 39

Введение

Сухие строки уравнений –

В них сила разума влилась.

В них объяснение явлений,

Вещей разгаданная связь.

Л.М.Фридман [10,268].

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. При изучении любой темы уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся.[10,241].

Автором данной работы выбрана тема «Формирование умения решения квадратных уравнений в 8 классе», так как она актуальна в современном мире; это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.

Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений. К изучению темы «Квадратные уравнения» учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. В значительной мере именно на материале данной темы осуществляется синтез материала, относящегося к уравнениям.

Исходя из вышесказанного, автор, выбирая тему курсовой работы, руководствовался ее значимостью и сложностью при обучении учащихся решению квадратных уравнений разного вида.

Цель работы: формирование представлений о работе над квадратными уравнениями на уроках математики. Исходя из данной цели, были поставлены следующие задачи:

• изучить научно-методическую литературу, касающуюся изучению уравнений;

• проанализировать школьные учебники и выделить в них место уравнений.

• разработать уроки по данной теме.

Для решения вышеуказанных задач были изучены следующие литературные источники:

1) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. – 2-е изд. – М.: Просвещение, 2003. – 287 с.

2) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 10-е изд. – М.: Просвещение, 2003. – 255с.

3) Мордкович А.Г.. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.

4) Бекаревич А.Б. Уравнения в школьном курсе математики. – М., 2000. – 241с.

5) Глейзер Г.И. История математики в школе VII – VIII классы. – М., 1982.

6) Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 2002.

7) Маркушевич Л.А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы // Математика в школе. – 2001. — №1. – с.15

8) Методика и технология обучения математике. Курс лекций: пособие для вузов / под ред. Н.Л.Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с.

9) Мишин В.И. Методика преподавания математики в средней школе. – М.,1999.- 398с.

10) Оганесян В.А. Методика преподавания математики в средней школе. – М.: Просвещение, 2003. – 368 с.

Проанализировав некоторые источники, можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе.

Объект исследования работы: процесс обучения математике.

Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса.

Контингент: учащиеся 8-го класса.

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1. Из истории возникновения квадратных уравнений

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:

(10+x)(10—x) =96,

или же

100 —x² = 96.

x² — 4 = 0

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:

y (20-y)=96

y² — 20y+96=0

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax² + bх = с, а> 0. (1)

В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

Задача 3.

«Обезьянок резвых стая

А двенадцать по лианам

Всласть поевши, развлекалась

Стали прыгать, повисая

Их в квадрате часть восьмая

Сколько ж было обезьянок,

На поляне забавлялась

Ты скажи мне, в этой стае?»

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.

Соответствующее задаче 3 уравнение:

,

Бхаскара пишет под видом:

x² — 64x = — 768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32², получая затем:

x² — б4х + 32² = -768 + 1024,

(х — 32)² = 256,

х — 32= ±16,

x₁ = 16, x₂ = 48.

Квадратные уравнения у Аль-Хорезми

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1. «Квадраты равны корням», т. е. ах² = bх.

2. «Квадраты равны числу», т. е. ах² = с.

3. «Корни равны числу», т. е. ах = с.

4. «Квадраты и числа равны корням», т. е. ах² + с = bх.

5. «Квадраты и корни равны числу», т. е. ах² + bх =с.

6. «Корни и числа равны квадратам», т. е. bх + с == ах².

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Приведем пример.

Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х² + 21 = 10х).

Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]

Квадратные уравнения в Европе XII—XVII в.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV—XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x² + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.[5,12].

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.

Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.

1.2. Основные направления изучения линий уравнений в школьном курсе алгебры

Уравнение как общематематическое понятие многоаспектно. Можно выделить главные области возникновения и функционирования понятия «уравнение» как:

• средства решения текстовых задач;

• особого рода формулы, служащей в алгебре объектом изучения;

• формулы, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением.[12,268]

Каждое из этих представлений оказалось в том или ином отношении полезным.

Названным областям относятся три основных направления изучения линий уравнений в школьном курсе алгебры.

1. Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время, ведущее положение в приложениях математики занимает математическое моделирование (Математическое моделирование заключается в конструировании по определенным правилам некоторой формальной системы, которая отображает через совокупность математических операций над величинами определенную гипотезу о структуре или воспитания). Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании. [14,246].

2. Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах:

• выделение и изучение наиболее важных классов уравнений, и их систем;

• изучение обобщенных понятий, относящихся ко всей линии в целом.

Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений.

3. Направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией, причем эта связь — двусторонняя. Основная идея, реализуемая в процессе установления взаимосвязи этих линий,— это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений.

Например, введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х² = b, где b—неотрицательное рациональное число, но и любых квадратных уравнений с рациональными коэффициентами и неотрицательным дискриминантом.[9,341]

Линия уравнений тесно связана также и с функциональной линией. Одна из важнейших таких связей — приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т. д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений , так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений и их систем.[12,269]

Изучение и использование преобразований уравнений и их систем, с одной стороны, предполагают достаточно высокую логическую культуру учащихся, а с другой стороны, в процессе изучения и применения таких преобразований имеются широкие возможности для формирования логической культуры.

Таким образом, владение содержанием линии уравнений позволяет расширить список выполнимых преобразований. Так, умение решать квадратные уравнения позволяет осуществлять сокращение дробей, в числителе или знаменателе которых имеется квадратный трехчлен. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.

1.3. Методика изучения квадратных уравнений

С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений.

Умение решать квадратные уравнения служит базой для решения других уравнений и их систем (дробных рациональных, иррациональных, высших степеней).

Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:

• формулу нахождения дискриминанта;

• формулу нахождения корней квадратного уравнения;

• алгоритмы решения уравнений данного вида.

уметь:

• решать неполные квадратные уравнения;

• решать полные квадратные уравнения;

• решать приведенные квадратные уравнения;

• находить ошибки в решенных уравнениях и исправлять их;

• делать проверку.

Решение каждого уравнения складывается из двух основных частей:

• преобразования данного уравнения к простейшим;

• решения уравнений по известным правилам, формулам или алгоритмам.

При изучении темы «Квадратные уравнения» рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А.Г.Мордкович, С.М.Никольский, Ю.Н.Макарычев, М.И.Башмаков.

Анализ учебников

А.Г. Мордкович

С.М. Никольский

Ю.Н. Макарычев

М.И. Башмаков

1.

—

2.Неполные квадратные уравнения

1.

—

2.Неполные квадратные уравнения

1.

—

2.Неполные квадратные уравнения

1.Историческая справка

2.Неполные квадратные уравнения

3.Полные квадратные уравнения

3.Полные квадратные уравнения

3.Полные квадратные уравнения

3.Полные квадратные уравнения

4.Приведенные квадратные уравнения

4.Приведенные квадратные уравнения

4.Приведенные квадратные уравнения

4.Приведенные квадратные уравнения

5.Теорема Виета

5.Теорема Виета

6.Теорема, обратная теореме Виета

6.Теорема обратная теореме Виета

Исходя из таблицы можно сделать вывод о том, что в учебниках алгебры разных авторов есть сходства и различия. Во всех современных школьных учебниках алгебры методическая линия изучения квадратных уравнений одинакова. В учебнике под ред. М.И.Башмакова дается историческая справка, а в других учебниках этого нет. В учебниках алгебры С.М.Никольского и Ю.Н.Макарычева при изучении темы «Квадратные уравнения» рассматриваются прямая и обратная теорема Виета.

Обучение решению уравнений начинается с простейших их видов, и программа [4,131] обусловливает постепенное накопление как их видов, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. В курсе математики старших классов учащиеся сталкиваются с новыми классами уравнений, систем или с углубленным изучением уже известных классов. Однако это мало влияет на уже сформированную систему знаний, умений и навыков; они дополняют ее новым фактическим содержанием.

Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:

I этап – «Решение неполных квадратных уравнений».

II этап – «Решение полных квадратных уравнений».

III этап – «Решение приведенных квадратных уравнений».

На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах² = 0, ах² + с = 0, где с≠ 0, ах² + bх = 0, где b ≠ 0. Рассмотрим решение несколько таких уравнений:

1. Если ах² = 0. Уравнения такого вида решаются по алгоритму:

1) найти х²;

2) найти х.

Например, 5х² = 0 . Разделив обе части уравнения на 5 получается: х² = 0, откуда х = 0.

2. Если ах² + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:

1) перенести слагаемые в правую часть;

2) найти все числа, квадраты которых равны числу с.

Например, х² — 5 = 0,Это уравнение равносильно уравнению х² = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два и — . Таким образом, уравнение х² — 5 = 0 имеет два корня: x₁ = , x₂ = — и других корней не имеет.

3. Если ах² + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:

1) перенести общий множитель за скобки;

2) найти x₁, x₂.

Например, х² — 3х = 0. Перепишем уравнение х² – 3х = 0 в виде х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x₁ = 0, x₂ = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х ( х – 3 ) = 0 получится число, не равное нулю.

Итак, данные примеры показывают, как решаются неполные квадратные уравнения:

1) если уравнение имеет вид ах² = 0, то оно имеет один корень х = 0;

2) если уравнение имеет вид ах² + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x₁ = 0; x₂ = — ;

3) если уравнение имеет вид ах² + с = 0, то его преобразуют к виду ах² = — с и далее х².= — В случае, когда — < 0, уравнение х² = — не имеет корней (значит, не имеет корней и исходное уравнение ах² + с = 0). В случае, когда — > 0, т.е. — = m , где m>0, уравнение х² = m имеет два корня

= , = -, (в этом случае допускается более короткая запись = .

Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.

На втором этапе осуществляется переход к решению полного квадратного уравнения. Это уравнения вида ах² + bx + c = 0, где a,b,c – заданные числа, а ≠ 0, х – неизвестное.

Любое полное квадратное уравнение можно преобразовать к виду , для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассмотриваются следующие случаи решения полных квадратных уравнений: D < 0, D = 0, D > 0.

1. Если D < 0, то квадратное уравнение ах² + bx + c = 0 не имеет действительных корней.

Например, 2х² + 4х + 7 = 0. Решение: здесь а = 2, b = 4, с = 7.

D = b² – 4ас = 4² – 4*2*7 = 16 – 56 = — 40.

Так как D < 0, то данное квадратное уравнение не имеет корней.

2. Если D = 0, то квадратное уравнение ах² + bx + c = 0 имеет один корень, который находится по формуле .

Например, 4х – 20х + 25 = 0. Решение: а = 4, b = — 20, с = 25.

D = b² – 4ас = (-20) ² – 4*4*25 = 400 – 400 = 0.

Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле . Значит,

3. Если D > 0, то квадратное уравнение ах² + bx + c = 0 имеет два корня, которые находятся по формулам: ; (1)

Например, 3х² +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b² – 4ас = 8² – 4*3*(-11) = 64 + 132 = 196.

Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:

.

Составляется алгоритм решения уравнения вида ах² + bx + c = 0.

1. Вычислить дискриминант D по формуле D = b² – 4ас.

2. Если D < 0, то квадратное уравнение ах² + bx + c = 0 не имеет корней.

3. Если D = 0, то квадратное уравнение имеет один корень, который находится по формуле

4. Если D > 0, то квадратное уравнение ах² + bx + c = 0 имеет два корня: ; .

Это алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому алгоритму не решают.

Математики – люди практичные, экономные, поэтому пользуются формулой: . (2)

Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно – записать сразу формулу (2) и с ее помощью делать необходимые выводы. [1,98].

На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х² +px + q = 0 (3), где p и q – данные числа. Число p – коэффициент при х, а q – свободный член. Дискриминант уравнения равен: D = p² – 4q. Рассматривают 3 случая:

1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле . (4)

2. D = 0, тогда уравнение (3) имеет единственный корень, или, как горят, два совпадающих корня:

3. D < 0, то уравнение не имеет корней. Обычно в случае приведенного квадратного уравнения (3) вместо D рассматривается выражение , имеющее тот же знак, что и D. При этом формулу корней приведенного квадратного уравнения (4) записывают так:

Отсюда следует, что:

1. если то уравнение (3) имеет два корня;

2. если то уравнение имеет два совпадающих корня;

3. если то уравнение не имеет корней.

Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения.

Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Иначе говоря, если x₁ и x₂ — корни уравнения х² +px + q = 0, то

x₁ + x₂ = — p,

x₁ x₂ = q. (5)

Данные формулы называют формулами Виета в честь французского математика Ф.Виета (1540-1603), который ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.

Например, приведенное уравнение х² — 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Справедлива также теорема, обратная теореме Виета.

Теорема, обратная теореме Виета. Если для чисел x₁, x_2, p, q справедливы формулы (5), то x₁ и x₂ — корни уравнения х² +px + q = 0 [2,49].

Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.

Например. Напишем приведенное квадратное уравнение, корнями которого являются числа 1 и -3.

По формулам Виета

– p = x₁ + x₂ = — 2,

q = x₁ x₂ = -3.

Следовательно, искомое уравнение имеет вид х² + 2х – 3 = 0.

Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего, требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной — только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета.

Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители

Таким образом, неполные и приведенные квадратные уравнения имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев. Обычно они изучаются перед выводом корней общего квадратного уравнения. В целом можно сказать, что освоение темы «Квадратные уравнения» поднимает учащихся на качественно новую ступень овладения содержанием школьной математики.

Глава 2. Методико-педагогические основы обучения решению квадратных уравнений

2.1. Урок – лекция по теме «Формула корней квадратного уравнения с четным вторым коэффициентом»

Цели:

• научить детей решать квадратные уравнения по новой формуле;

• повторить ранее изученный материал по теме «Квадратные уравнения»;

• развивать вычислительные навыки детей, внимание, память, математическую речь;

• воспитывать аккуратность, умение аргументировать свою точку зрения.

Оборудование: карточки с формулами.

Ход урока

1. Домашнее задание.

— Откройте дневники, запишите домашнее задание: учить формулы, вывод этих формул.

2. Устные упражнения.

— В начале урока повторим теоретический материал по теме: «Квадратные уравнения».

2.1. Фронтальный опрос.

1. Что называют квадратным уравнением? (Квадратным уравнением называют уравнение вида вид ах² + bx + c = 0, где а, b, c – любые действительные числа, причем а ≠ 0).

2. В уравнении 2х +4х² +1 = 0 (на доске).

— Назовите: — старший коэффициент (4);

— второй коэффициент (2)

— свободный член (1).

3. Какое уравнение называют приведенным квадратным уравнением? Пример. (Квадратным уравнение называют приведенным, если старший коэффициент равен 1. Пример: х² + 3х + 4 = 0).

4. Какое уравнение называют полным квадратным уравнением? (Полным квадратным уравнением называют уравнение, в котором присутствуют все три слагаемых, т.е. уравнение, где b, c ≠ 0).

5. Какое уравнение называется полным квадратным уравнением? (Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых).

6. Что называют корнем квадратного уравнения? (Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трехчлен ах² + bx + c = 0 обращается в нуль; такое значение переменной х называют корнем квадратного трехчлена).

7. Что значит решить квадратное равнение? (Значит, найти все его корни или установить, что корней нет).

3. Сообщение темы и цели урока.

— Сейчас мы познакомимся еще с одной формулу, по которой можно найти корни квадратного уравнения.

— Будем учиться применять ее при решении квадратных уравнений.

4. Работа по теме урока.

4.1. Историческая справка.

— Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 400 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развитие математики, был французский математик Виет. Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел

4.2. Объяснение нового материала.

— Записываем в тетрадях для лекций сегодняшнее число и тему нашего урока: «Формула корней квадратного уравнения с четным вторым коэффициентом».

— Все внимательно слушаем, в тетрадь пока ничего не пишем.

Слова учителя Записи на доске

1. Пусть дано квадратное уравнение ах² + bx + c = 0

ах² + bx + c = 0, со вторым четным b = 2n. коэффициентом, т.е. b = 2n.

— Тогда уравнение можно записать ах² + 2nx + c = 0 в виде:

— Найдем дискриминант (вместо b D = (2n) ² – 4ас = пишем 2n).

— Что получили?

— Что я могу сделать с этим выражением? = 4n² – 4ас =

(раскрыть скобки)

— Что получиться?

— А дальше можно 4 – вынести за скобки. = 4(n² – ас)

— Выражение в скобках обозначим через n² – ас = D₁

D.

— Запишите в тетрадь мои записи с доски.

2. – От чего зависит количество корней в D = 4(n² – ас) = 4D₁

квадратном уравнении? (от значения D).

— От чего зависит значение D? (от значения D₁)

— Пусть D > 0, тогда D₁ >0 и D = 4D₁> 0 D₁ >0

— Чему равно D? (4D₁)

— Что можно сделать дальше? (вынесем 2 из-под знака корня).

— Еще что можем сделать? (вынести общий множитель за скобки и сократить)

— Кто может записать, чему равно x₂.

Микрообобщение: таким образом, если

— Запишите в тетрадь, как мы нашли х₁ и х₂ .

3. Если D₁ = 0, то D = 0. D₁ = 0

— Сколько корней имеет квадратное уравнение? (один корень).

— По какой формуле его можно найти?

— т.к. b = 2n, подставим вместо b → 2n.

Таким образом, если D₁= 0, то

— Запишите в тетрадь!

4. Если D₁ < 0, то и D < 0. D₁ < 0

— Что известно о корнях? (корней нет) корней нет

5. Рассмотрим эту формулу для х² + 2nx + c = 0 приведенного квадратного уравнения.

— Какую формулу корней квадратного уравнения мы получим?

а = 1.

— Запишите!

— Внимательно посмотрите, какие есть вопросы?

4.3. Итог: мы познакомились с новой формулой, которая в некоторых случаях облегчает нам расчеты.

4.4. Закрепление нового материала.

а) Решаем вместе, один ученик у доски: х² – 2,4х +1 = 0

b = 2,4; n = — 1,2

D₁ = n² – ас

D₁= 1,44 – 1 = 0,44

Ответ:

б) х² + 6х + 8 = 0

b = 6, n = 3

D₁ = n² – ас

D₁ = 3² – 1*8 = 9 – 8 = 1

=-4

Ответ: x₁ = — 4, x₂ = — 2.

в) 3х ² – 3х + 4 = 0 (самостоятельно)

— Корни этого уравнения можно найти по новой формуле? (нет, т.к. b – число нечетное).

— Решаем уравнение по известной вам уже формуле.

3х ² – 3х + 4 = 0

D = 9 – 4 * 3 * 4 = 9 – 48 = — 39

D<0 > решений нет.

5. Итог урока.

-Что нового узнали сегодня на уроке?

2.2. Урок – практикум по теме «Решение квадратных уравнений» [16,22]

Цели урока:

• отработка общих умений и навыков при решении квадратных уравнений;

• развитие внимания, навыков самоконтроля и самооценки.

Оборудование: карточки для самостоятельной работы.

Ход урока:

1.Организационный момент (1 мин)

Сообщение темы и цели – повторим, то, что необходимо знать при решении квадратных уравнений; проверим свои умения решать квадратные уравнения в самостоятельной работе.

2. Разминка (6 мин)

2.1. Игра «Заполни квадрат». (Упражнение на развитие памяти и внимания). За 10 секунд запомнить, что записано в клетках квадрата, и записать в свой квадрат.

А

Р

У

Е

Н

В

Е

И

Н

Зашифровано слово «УРАВНЕНИЕ»

1.2. Историческая справка. Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 400 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развитие математики, был французский математик Виет. Имя этого математика нам скоро встретится.

1.3. Повторяем теоретические вопросы (у доски один человек). Записан ход решения квадратного уравнения; ученик рассказывает, остальные записывают алгоритм.

3. Повторение (фронтальный опрос 6 мин)

3.1. Вычислите:

а) -4*1*(-4), -4*2*5, -5*6*4;

б) (-10)², 3 ² , (-7) ²

Это нужно уметь при нахождении дискриминанта D.

в) У доски два ученика; правило сложения чисел с разными знаками, правило сложения отрицательных чисел:

г) ,,,. (при нахождении корней).

3.2. Игра «Срочная радиограмма». Класс делится на две команды: девочки – мальчики. В двух конвертах – отдельные слова. Задача: составить одно математическое предложение из имеющихся слов. Трудность состоит в том, что одного слова не хватает.

«Если ДИСКРИМИНАНТ больше нуля, то уравнение имеет два различных корня»;

«Если квадратное уравнение в СТАНДАРТНОМ виде, то можно находить дискриминант».

4. Тестовые вопросы (5 мин)

На доске 8 квадратных уравнений. Эти задания на слух, повторяются только два раза. Залог успеха – огромное внимание.

1. 2х² – 8х +4 = 0; 5. 5х²+ 6х = 0;

2. 3х² + 4х — 1 = 0; 6. х² – 8х + 12 = 0;

3. 4х² – 8 = 0; 7. 3х² = 0;

4. х² – 10х + 100 = 0; 8. 14 – 2х² + х = 0

а) Выпишите номера полных квадратов уравнений

б) Выпишите коэффициенты а, b, c в уравнении 8.

в) Выпишите номер неполного квадратного уравнения, имеющего один корень.

г) Выпишите коэффициенты a, b, c в уравнении 5.

д) Найдите дискриминант в уравнении 6.

е) Найдите дискриминант в уравнении 4 и сделайте вывод о количестве корней.

Проверяем, оцениваем себя сами:

нет ошибок – «5»

1 – 2 ошибки – «4»

3 – 4 ошибки – «3»

5. Игра « Следствие ведут знатоки » ( 10 мин )

Прежде чем доверить расследование серьезного дела, необходимо пройти проверку.

а) Сможете ли вы отыскать ошибку в решении уравнения?

— х² + 6х + 16 = 0,

х² – 6х – 16 = 0,

a = 1, b = — 6, c = — 16.

D = b² – 4ac = ( — 6)² – 4 * 1 * ( — 16) = 36 +64 = 100

Ошибку ищем по этапам, с самого начала.

б) Самым трудным и важным делом каждого ученика является выполнение домашнего задания. Если домашнее задание выполнено правильно, то на уроке вы чувствуете себя гораздо увереннее. Домашнее задание спрятано в кабине, предлагается его найти. Будем действовать, как настоящие знатоки: четко и слаженно. У нас две бригады следователей. Я даю вам небольшую зацепку в деле. Бригада, которая будет действовать дружно, первой справится заданием:

Если вы, верно решите квадратное уравнение

х² – 7х + 10 = 0,

то х укажет номер ряда, а х – номер парты, где находится домашнее задание.

[5;2]

в) Записываем найденное задание:

2х ²+ 7х – 74 = 0.

Вычислите дискриминант. Это и есть номер задания в учебнике. В этом задании восемь уравнений. Можно решить любое количество.

6.Самостоятельная работа (12 мин)

Выполнив самостоятельную работу, вы узнаете, можете ли решать квадратные уравнения без ошибок.

Первые два уравнения можно проверить (решения на оборотной стороне доски). Третье уравнение, если будет время, проверьте сами по определению корня.

1. х² + 2х – 25 = 0.

2. 9х² – 6х + 1 = 0.

3. 3х² + 8х – 3 = 0.

7. Подведение итогов урока.

2.3. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» [13,14]

Цели урока:

• закрепить практические и теоретические знания и умения учащихся при выполнении заданий по теме «Квадратные уравнения»;

• развивать самостоятельность, активность, внимание;

• воспитывать интерес к предмету.

Оборудование: звездочки, таблицы с цифрами.

Ход урока:

1.Организация класса

а) Приветствие

б) Проверка готовности рабочих мест

2. Сообщение темы и цели урока

-Сегодня у нас особенный урок, мы проведем с вами «Звездный час» по теме «Квадратные уравнения», тем самым еще раз проверим свои знания и умения.

3. Закрепление материала

3.1. Знакомство с правилами игры.

— Итак, представим, что мы с вами в студии. Вы игроки, а я ведущая. У вас у каждого на партах лежат таблички с цифрами от 1 до 5.

1

2

3

4

5

— Итак, послушайте условия игры.

— Я буду задавать всем вопросы, а соответственно поднимать табличку с тем номером, который соответствует правильному ответу. А так же у каждого из вас лежат на партах листочки. За каждый правильный ответ, когда я вам скажу, вы будете на нем чертить звездочку. А в конце игры мы их подсчитаем и оценим работу каждого из вас.

3.2. Проведение игры.

— Итак, начинаем игру. Сейчас мы будем работать с вами по 1 таблице

Таблица №1

1

2

3

4

5

-Итак, сверху вы видите номера ответов, а под ними соответствующие ответы. Я задаю вопрос, вы 5 секунд, думаете и поднимаете таблички с правильными ответами.

1. Какой вид имеет квадратное уравнение.

2. Назовите формулы корней квадратного уравнения.

3. Назовите неполное квадратное уравнение.

4. Назовите, чему равен дискриминант квадратного уравнения.

-Хорошо с этим заданием вы справились хорошо, почти все учащиеся поднимали таблички с правильными ответами. А кто ошибался, он еще раз увидел правильные формулы и надеюсь, так же доучит материал.

-А теперь мы все переходим во второй тур. Во втором туре мы выясним знание правил по данной теме. Работать будем со второй таблицей.

Таблица №2

1

2

3

4

5

Теорема обратная теореме Виета

Квадратное уравнение

Теорема Виета

Неполное квадратное уравнение

Приводимое квадратное уравнение

-Я буду говорить вам правило, а вы поднимайте соответствующую карточку.

1. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

-Верно, следующий вопрос, слушайте и поднимайте таблички.

1. Если в квадратном уравнении хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется….

-Верно, приведите пример квадратного уравнения.

2. Уравнение вида , где х переменная, а, в, с – некоторые числа, причем а  0 называется….

-Верно, приведите пример квадратного уравнения

Следующий вопрос

3. Если числа м и n таковы, что их сумма равна р, а произведение q, то эти числа являются корнями уравнения вида

-Верно, скажите, сколько корней имеет неполное квадратное уравнение каждого вида.

-Верно.

4. Как называются полные квадратные уравнения, у которых все три коэффициента отличны от нуля и в которых первый коэффициент равен 1.

-Хорошо и с этим заданием вы справились.

4. Самостоятельная работа. (Третий тур).

-Вам в этом туре необходимо выполнить следующие задания. На доске выписаны квадратные уравнения.

1. х² – 15х – 16 = 0.

2. х² – 9х + 20 = 0.

3. 2х² + 2х – 112 = 0.

4. х² – 6х + 8 = 0.

-Вы самостоятельно решаете эти уравнения в тетради, а потом мы проверим.

-Итак, я буду называть вам уравнения, а вы поднимайте карточку, соответствующую правильному ответу.

-Хорошо давайте проверим.

-Поднимите карточку, соответствующую правильному ответу для уравнения 2х² + 2х – 112 = 0.

-А теперь составьте три неполных квадратных уравнения и решите их.

-Давайте посмотрим, какие уравнения вы составили

5. Подведение итогов

-Итак, вот и подходит к концу наша игра. В ходе игры мы повторили теоретический и практический материал, и теперь мы можем подвести урок игры. Подсчитайте свои звездочки

-Кто набрал от 20 до 25 звезд получают «5»

-Кто набрал от 20 до 15 звезд получают «4»

-Кто набрал 15 звезд и меньше получают «3»

Заключение

Автором была выполнена курсовая работа по теме «Формирование умения решения квадратных уравнений в 8-ом классе». При выполнении данной работы понадобились не только те знания, которые имеются у самого автора, но и необходимая работа с дополнительной литературой, составление конспектов уроков.

Благодаря выполнению этой работы можно сказать, что материал, связанный с уравнениями, составляет значительную часть школьного курса математики. На изучение темы «Квадратные уравнения» по программе дается всего 22 ч. Их изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования: прикладная направленность, теоретико-математическая направленность и направленность на установление связей с остальным содержанием курса математики.

Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению темы «Квадратные уравнения» учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. владение содержанием линии уравнений позволяет расширить список выполнимых преобразований. Так, умение решать квадратные уравнения позволяет осуществлять сокращение дробей, в числителе или знаменателе которых имеется квадратный трехчлен. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.

Список литературы

1) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. – 2-е изд. – М.: Просвещение, 2003. – 287 с.

2) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 10-е изд. – М.: Просвещение, 2003. – 255с.

3) Башмаков М.И. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.

4) Бекаревич А.Б. Уравнения в школьном курсе математики. – М., 1968.– 196 с.

5) Бурмистрова Т.А. Программы общеобразовательных учреждений // Математика.- М.: Просвещение,1994.

6) Глейзер Г.И. История математики в школе VII – VIII классы. – М., 1982.

7) Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 1977.

8) Лягущенко Е.И. Методика обучения математике в 5 кл. – Минск, 1976.

9) Маркушевич Л.А., Черкасов Р.С. Уравнения и неравенства в заключительном повторении курса алгебры средней школы // Математика в школе. – 1994. — №1. – с.

10) Методика и технология обучения математике. Курс лекций: пособие для вузов / под ред. Н.Л.Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с.

11) Мишин В.И. Методика преподавания математики в средней школе. – М.,1990.

12) Оганесян В.А. Методика преподавания математики в средней школе. – М.: Просвещение, 1980. – 368 с.

13) Панкратова Л. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» // Математика.-2002.-№21.

14) Сабинина Л.В. Методика в понятиях и терминах. Ч.1. – М.: Просвещение, 1978. – 320 с.

15) Столяр А.А. Общая методика преподавания математики. – М., 1985.

16) Шаталова С. Урок – практикум по теме «Квадратные уравнения».- 2004. -№42