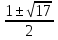Муниципальное бюджетное общеобразовательное
учреждения гимназия № 19 им.Н.З.Поповичевой
г.Липецка
Урок алгебры по теме:
«Теорема Безу и следствие из неё»
(профильный уровень)
/11 класс/
Подготовила
учитель математики
Маликова Ольга Георгиевна
Тема: «Теорема Безу и следствие из неё»
(алгебра, 11 класс)
Цели урока:
Дидактические: — развитие навыков использования схемы Горнера
— доказательство теоремы Безу и следствия из неё при
решении проблемной ситуации: можно ли разложить
многочлен третьей степени на множители;
— использование теорему Безу для решения уравнений высших
степеней;
— закрепление применения данной теоремы и следствия из неё
в ходе решения задач.
Развивающие: — продолжение развития логического мышления и
мировоззрения учащихся.
Воспитательные: — воспитание творческого мышления, познавательной
активности, смелости своих суждений, культуры речи;
Тип урока: урок открытия «нового знания» (использование технологии проблемно-диалогового обучения)
Оборудование: мультимедийная установка.
Ход урока: 1. Организационный момент.
2. Актуализация знаний.
3. Изучение нового.
4. Историческая справка.
5. Закрепление.
6. Итог урока.
Ход урока
1. Организационный момент
Здравствуйте ребята.
Слайд 1 «Метод решения хорош, если с самого начала мы можем предвидеть — и далее подтвердить это, — что, следуя этому методу, мы достигнем цели»
(Г. Лейбниц) Именно эти слова будут лежать в основе нашего сегодняшнего урока.
И сегодня мы продолжим разговор об одном из важнейшем понятии математики — уравнении. На протяжении веков выдающиеся математики развивали теорию решения алгебраических уравнений.
Слайд 2 Среднеазиатский математик ал-Хорезми в IX веке установил, что решение уравнений первой степени сводится к двум операциям. Каким?
(к переносу отдельных членов его из одной части равенства в другую и приведение подобных членов)
Уравнения второй степени умели решать еще вавилоняне во втором тысячелетии до нашей эры.
Для уравнений третьей и четвертой степени есть формулы корней (формулы Кордано и Феррари), выведенные итальянскими математиками в 1545 году, но в силу своей громоздкости эти формулы не используют в школьной программе. После того, как были выведены формулы корней для уравнений третьей и четвёртой степени, на протяжении почти 300 лет, учёные-математики пытались вывести формулы для нахождения корней уравнений пятой степени и выше, но труды их оказались безуспешными.
Слайд 3 В 1826 году норвежский математик Абель доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше.
— Что же делать? Неужели уравнения степени выше 2 невозможно решить? Конечно же можно.
2. Актуализация знаний
И какие методы для решения уравнений высших степеней мы знаем?
Слайд 4(метод разложения на множители, замена переменной, функционально-графический метод)
3. Изучение нового
Слайд 5
— Решить уравнение x3 + 2x2 — 7x – 12 = 0. Можно ли известными методами разложить на множители левую часть уравнения.(Проблема!) Мы понимаем, что было бы удобно представить левую часть равенства в виде произведения, т.е. разложить на множители.
— Какие методы разложения на множители вы можете назвать?(вынесение общего множителя за скобок, способ группировки, ФСУ)
Нужно разложить многочлен 3 степени на множители. Но как?…
— Сегодня мы рассмотрим ещё один из методов разложения на множители и сформулируем алгоритм решения уравнений такого вида, а тему урока сформулируем в ходе урока.
Слайд 6
— Как разложить на множители квадратный трёхчлен ах2 + bх + с? (найти корни и воспользоваться формулой)
— А нам как раз необходимо разложить на множители многочлен Р(х) = x3 + 2x2 — 7x – 12. Для этого нужно найти его корни. Что называется корнем многочлена? (Число а называется корнем многочлена f, если f(а)=0).
— Сформулируйте теорему о нахождении целых корней многочлена( Пусть все коэффициенты многочлена Р(х) – целые числа. Если целое число а является корнем многочлена Р(х), то а – делить свободного члена многочлена Р(х))
— Найдите делители свободного члена (±1, ±2, ±3, ±4, ±6, ±12)
— Какое число является корнем многочлена? (х = -3 – корень многочлена)
— Значит один из множителей будет (х + 3). Как найти другие множители? (выполнить деление многочлена на двучлен (х + 3) по схеме Горнера). (1 ученик у доски)
— Обратите внимание, что х = -3 является корнем многочлена и при делении на (х + 3) получился остаток 0, т.е. чему равно значение многочлена при х = -3? (0)
Слайд 7
— Число х = 2 является корнем данного многочлена? (нет) Выполните деление многочлена на двучлен (х – 2). Получается деление с остатком, остаток равен -10. Найдите значение многочлена при х = 2. (1 ученик работает у доски) Значение многочлена равно -10. Отметим, что x=2- не является корнем многочлена и остаток от деления многочлена на (х-2) равен значению многочлена при х=2.
Аналогичная работа для х = 1; х = -2 (самостоятельно)
— Замечаете ли вы ту же закономерность (речь идет о значении остатка и значении многочлена при различных значениях х)?
— Сформулируйте гипотезу. (Обучающиеся формулируют гипотезы)
— Запишем её в общем виде.
Слайд 8
Пусть Р(х) — многочлен, а — некоторое число.
Докажем следующие утверждения:
1. Остаток от деления Р(х) на (x — а) равен Р(а).
2. Р(х) делится на двучлен (x — а) тогда и только тогда, когда число а является его корнем.
Доказательство (доказательство гипотезы): 1. по теореме о делении с остатком следует, что Р(х) = (х – а)Q(х) + г, где q(х) многочлен степени на 1 меньше чем Р(х), r – остаток (число). Подставим вместо х значение а, получим Р(а) = (а – а)q(х) + r = r. Ч.т.д.
— Эту теорему называют теоремой Безу в честь французского математика Этьена Безу.
— Итак сформулируйте теорему Безу.( Остаток отделения многочлена Р(х) ненулевой степени на двучлен х – а равен Р(а) (т.е. значению многочлена Р(х) при х = а)
Доказательство: 2. Если а – является корнем многочлена, то Р(а) = 0, следовательно г = 0 и многочлен примет вид Р(а) = (х – а)Q(х). Это значит, что многочлен Р(а) делится на (х – а).Ч.т.д
— Мы получили следствие из теоремы Безу. Сформулируйте его. (Если число а является корнем многочлена Р(х), то Р(х) делится на двучлен х — а.
4. Историческая справка
Этьен Безу- французский математик, член Парижской Академии Наук.
Именем учёного названа одна из основных теорем алгебры — ТЕОРЕМА БЕЗУ. Теорема Безу, несмотря на внешнюю простоту и очевидность, является одной из фундаментальных теорем теории многочленов. В этой теореме алгебраические свойства многочленов (которые позволяют работать с многочленами как с целыми числами) связываются с их функциональными
свойствами (которые позволяют рассматривать многочлены как функции).
Слайд 9
Вернёмся к нашему уравнению. Воспользуемся следствием из теоремы Безу и разложим левую часть уравнения на множители. (1 ученик у доски)
x3 + 2x2 — 7x – 12 = 0
(х + 3)(x2 – x — 4) = 0.
Слайд 10
Сформулируйте алгоритм решения уравнений с помощью теоремы Безу:
5. Закрепление
Слайд 11 Подумай и реши:
1) Найти остаток от деления многочлена x3 — 3x2 + 6x – 5 на двучлен (x — 2).
Решение:
r = P(2) = 23 — 3∙22 + 6∙2 — 5 = 3 .
2) При каком значении a многочлен x4 + ax3 + 3x2 – 4x – 4 делится без остатка на двучлен x – 2?
Решение:
По теореме Безу
r = P(2) = 16 + 8a + 12 – 8 – 4 = 8a +16.
Но по условию r = 0, значит 8a + 16 = 0, отсюда a = -2 .
3) Разложите на множители х4 + 324.
Решение: данный многочлен разложить на множители не возможно, т.к. он не имеет корней.
6. Итог урока
Теорема Безу находит применение при рассмотрении одной из важнейших задач математики — решении уравнений. Существует несколько следствий из теоремы, которые помогают при решении практических задач. Из рассмотренных примеров можно сделать вывод, что теорема Безу находит применение при решении задач, связанных с делимостью многочленов, например, нахождение остатка при делении многочленов. Также, теорема работает при разложении многочленов на множители.
Теорема Безу позволяет ответить и на важный теоретический вопрос — Сколько корней может иметь многочлен?
Слайд 12
Дома: Докажите утверждение: «Многочлен степени n имеет не более n корней».
(Воспользуйтесь методом от противного)
Список использованной литературы
1. А.Г.Мордкович, П.В.Семёнов. Алгебра и начала математического анализа
(профильный уровень), 11 класс. Ч. 1 – М: Мнемозина, 2009
Использованные Интернет-ресурсы
2. http://www.ref.by/refs/49/32199/1.html