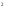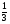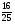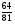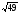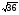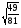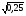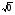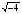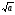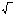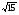ПЛАН-КОНСПЕКТ УРОКА
_____Арифметический квадратный корень_____________________________________
-
Борисова Мария Васильевна | |
-
| Место работы: МБОУ Гагинская СОШ | |
-
| Должность учитель | |
-
| Предмет алгебра | |
-
| Класс 8 | |
-
| Тема и номер урока в теме «Арифметический квадратный корень», 1урок | |
-
| Базовый учебник Алгебра.8класс. Ш.А.Алимов, Ю.М.Колягин и др. | |
-
Цель и задачи урока
Цель: Способствовать формированию у учащихся представления об определение арифметического квадратного корня и добиться усвоения учащимися навыка извлечения квадратного корня из числа
Задачи:
— образовательная задача – ученики должны знать:
1) фактический материал: возведение числа в квадрат; извлечение квадратного корня.
2) теоретический материал: знать понятие арифметического квадратного корня; понимать смысл существования арифметического квадратного корня.
-развивающая задача – ученики должны уметь:
— анализировать, делать выводы, логически мыслить;
— развивать творческую сторону мыслительной деятельности;
— создать условия для проявления познавательной активности учащихся
Надпредметные компетенции:
1) развитие речи,
2) развитие мышления,
3) развитие сенсорной сферы.
-воспитательная задача – ученики должны понимать:
— воспитывать культуру умственного труда;
— формировать умения трудиться, сотрудничать, сопереживать;
— требовательное отношение к себе;
— интерес к предмету.
-
Тип урока комбинированный
-
Формы работы учащихся фронтальная, самостоятельная, групповая
-
Необходимое техническое оборудование: компьютер, проектор, ноотбуки
-
Структура и ход урока
СТРУКТУРА И ХОД УРОКА
№
Этап урока | Название используемых ЭОР (с указанием порядкового номера из Таблицы 2) | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин.) |
| 1 | 2 | 3 | 5 | 6 | 7 |
| | Оргмомент | | Приветствует учащихся, определяет отсутствующих. Проверяет готовность к уроку. | | 2 |
| 1 | Мотивационно-ориентированная часть |
| 1.1 1.2 1.3 | Актуализация Цель: повторить действие возведения числа в квадрат, применение формулы разности квадратов. Мотивация Цель: установить недостаток знаний работы с числами, подвести к созданию проблемной ситуации. Постановка УЗ | Презентация «Арифметический квадратный корень» (1) | Готовит уч-ся к восприятию нового материала, дает задания на повторение (проецируется на экран): -
Вычислить: (слайд1) 3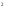 ; (-5) ; (-5) ; ( ; (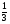 ) )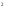 ; (0,9) ; (0,9)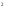 ; 10 ; 10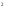 2.Представить число в виде произведения двух одинаковых множителей: 36; 81; 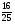 ; 0,01 ; 0,01 3. Разложить на множители: 4m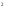 — — 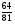 ; а ; а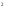 — 9. — 9. Учитель предлагает вспомнить формулу нахождения площади квадрата и решить устно задачи: (слайд2) 1.Найти площадь квадрата сторона, которого равна 4см. 2. Площадь земельного участка, имеющего форму квадрата, равна 49 м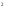 . Чему равна длина его стороны? . Чему равна длина его стороны? 3. Найдите сторону квадрата, площадь которого равна 15 м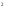 . . — Чем мы должны заняться на сегодняшнем уроке? | Выполняют самостоятельно в тетрадях, с последующей проверкой Учащиеся вспоминают формулу нахождения площади квадрата, применяя ее решают 1, 2 задачи. Третью задачу решить не могут, т.к. не знают числа, квадрат которого равен 15. (появляется затруднение в решении задачи, проблемная ситуация) Ставят задачу урока: выявить операцию, обратную возведения числа в квадрат. Научиться применять ее в различных ситуациях.(совместно с учителем) | 3 3 2 |
| 2 | Операционно- исполнительская часть |
| 2.1 2.2 2.3 2.4 | Решение УЗ Первичное закрепление Цель: проверить усвоение определения арифметического квадратного корня Отработка правила Включение в систему знаний и повторение | Презентация «Арифметический квадратный корень» (1) Тест 1 (2) Тест 2 (3) | Предлагает вернуться к задаче 2 из мотивации. Задача была решена с помощью подбора, а нельзя ли решить ее алгебраическим способом? (слайд 3,4) Вопрос: Сколько корней имеет уравнение, и какими числами они записаны? Какое число будет записано в ответ задачи? — Найденные числа 7 и -7 называются квадратными корнями из числа 49. Положительный корень 7 называют – арифметическим квадратным корнем из числа 49. Обозначают 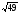 . . 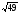 = 7 (слайд 5) = 7 (слайд 5)
Предлагает сформулировать определение арифметического квадратного корня. — Сравните ваше определение с определением в учебнике. Вводит знак арифметического квадратного корня, и что называется подкоренным выражением Дает задание: (слайд6) а) Вычислить устно: 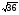 ; ; 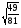 ; ; 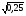 ; ; 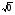 ; ;
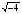
б) Верно ли равенство: 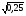 = — 0,5? = — 0,5? — Какие условия должны выполняться, чтобы число являлось арифметическим квадратным корнем? — Действие нахождения квадратного корня из числа называется извлечением квадратного корня. Выражение 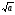 имеет смысл при а ≥ 0 имеет смысл при а ≥ 0 Определение квадратного корня: 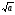 ≥ 0, ( ≥ 0, (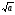 ) )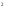 = а = а
(слайд 7) — Чему же равна сторона квадрата, площадь которого 15 м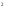 ? (слайд 8) ? (слайд 8) Учитель дает задания по учебнику №307, 309 Выполним задание на компьютере | Учащиеся обозначают сторону квадрата за x и записывают уравнение: S = х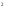 , , х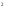 = 49 (работая в группе выбирают способ решения получившегося уравнения) = 49 (работая в группе выбирают способ решения получившегося уравнения) х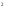 — 49 =0, — 49 =0, (х-7)(х+7)= 0 х=7, х= -7 -Два корня. Один положительный, а другой отрицательный. Положительный корень будет выражать длину квадрата. Учащиеся формулируют определение арифметического квадратного корня с коррекцией учителя Сравнивают и делают выводы Учащиеся совместно с учителем записывают: 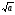 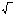 — радикал, арифметического квадратного корня — радикал, арифметического квадратного корня
а – подкоренное выражение Выполняют задание фронтально, обоснованно, например: 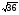 = 6, т.к. 6>0 и 6 = 6, т.к. 6>0 и 6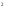 = 36 = 36 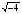 вычислить нельзя, т.к. нет такого числа, квадрат которого равен -4 вычислить нельзя, т.к. нет такого числа, квадрат которого равен -4
Учащиеся проговаривают и записывают вывод: 1.Число неотрицательное 2. Квадрат числа равен подкоренному выражению Учащиеся записывают в тетрадь. Учащиеся решают уравнение: х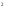 = 15 = 15 х = 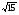 , т.к. ( , т.к. (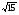 ) ) =15 =15  Выполняют в группе | 8 2 3 3 2 4 8 |
| 3. | Рефлексивно – оценочная часть |
| 3.1 3.2 | Итог урока Домашнее задание | | 1.Что открыли нового на уроке? 2.Какую задачу поставили в начале урока? Решили мы ее? 3. Чему научились? 3. Как я работал на уроке? — знать определения арифметического квадратного корня; что означает «извлечь квадратный корень»; №309-311(чет), (базовый) №311- 313 (чет) (повышенный) | 1.Получили определение арифметического квадратного корня. Выяснили, когда он определен. 2. Выявить операцию, обратную возведения числа в квадрат. Да. Узнали, что действие нахождения квадратного корня из числа, называется извлечением квадратного корня. 3. Научились извлекать квадратный корень. 4. Отвечают … Учащиеся записывают в дневник | 3 2 |
Таблица 2.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
№
Название ресурса | Тип, вид ресурса | Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.) | Гиперссылка на ресурс, обеспечивающий доступ к ЭОР |
| 1 | Презентация | Комбинированный | презентация | «Арифметический квадратный корень» |
| 2 | Тест 1 | Практический | тест | A08_022_p01.oms |
| 3 | Тест 2 | Контролирующий | тест | A08_022_k01.oms |