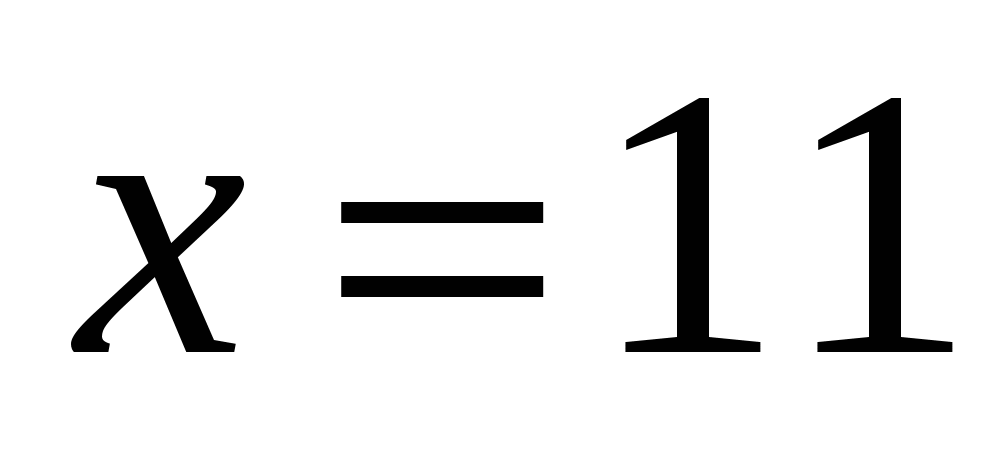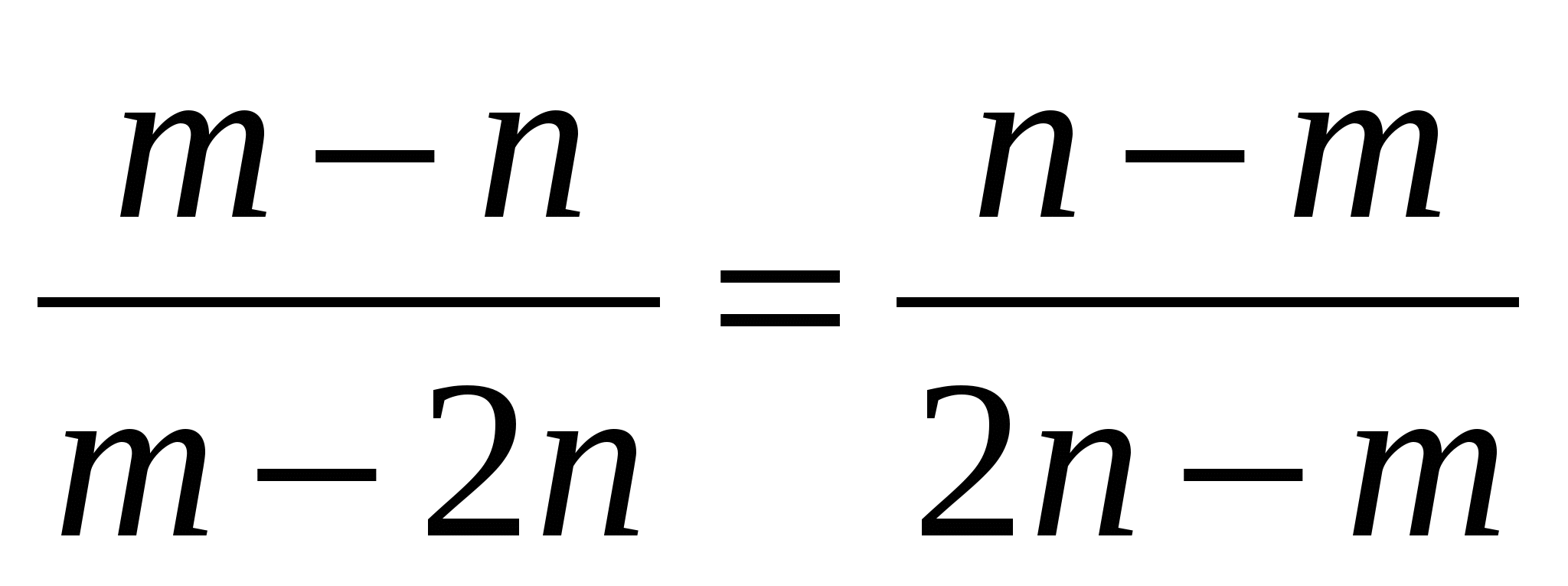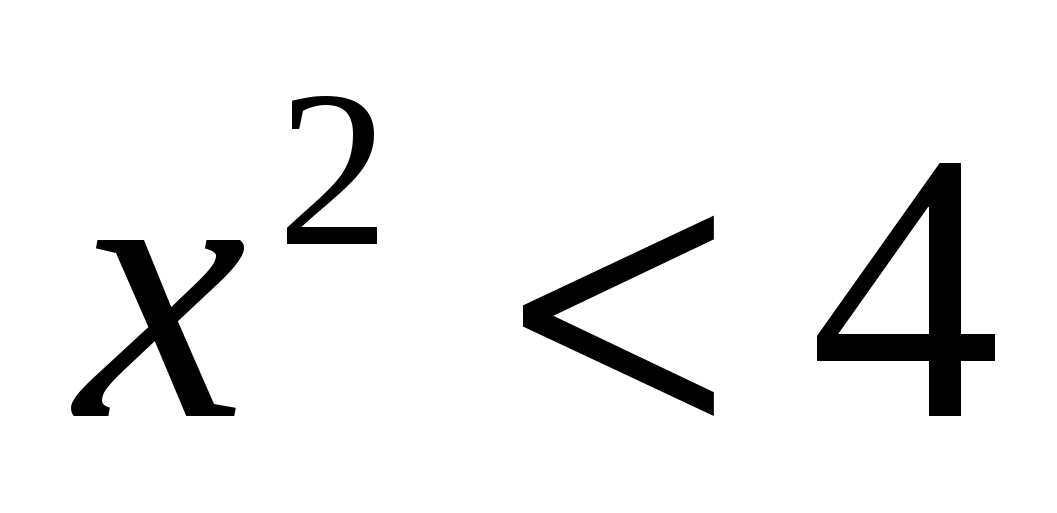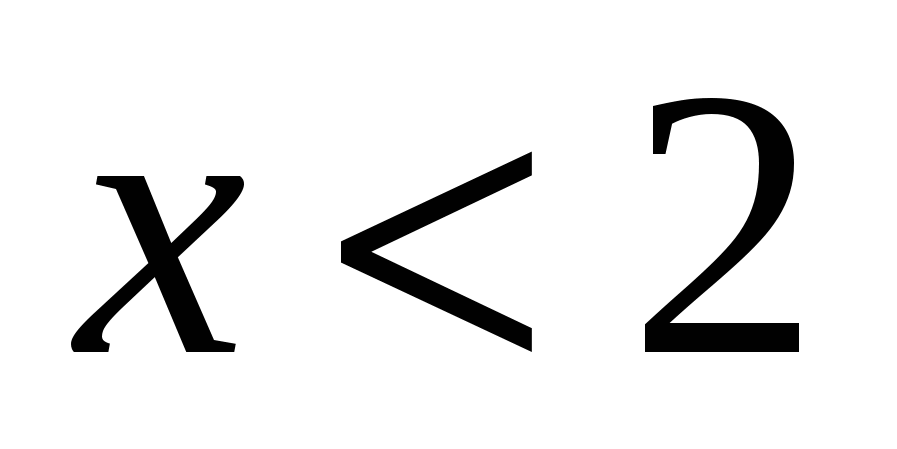Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №24
Методическая разработка урока
по алгебре для учащихся 9 класса
(углублённый уровень)
«Математический детектив»
Урок повторения темы
«Уравнения и неравенства»
Разработала:
Жилякова Ольга Владимировна
учитель математики МБОУ СОШ №24
1 квалификационная категория
тел. 6-40-22, 902-27-15-847
Асбестовский городской округ
2012
Пояснительная записка
Целью разработанного урока является создание условий для подготовки учащихся 9-го класса к государственной итоговой аттестации.
Задачи:
-
отрабатывать практические навыки и умения по теме: «Уравнения и неравенства», полученные на разных этапах обучения;
-
развивать коммуникативную компетентность через аргументацию и обоснования выдвинутых гипотез, проведение доказательных рассуждений;
-
показать ценность умения устанавливать партнёрские отношения друг с другом.
Планируемый результат:
-
отработаны практические навыки и умения по теме: «Уравнения и неравенства»;
-
усовершенствована коммуникативная компетентность;
-
продемонстрирована ценность умения устанавливать партнёрские отношения.
Условия для проведения урока: Данный урок проводится в конце учебного года, когда начинается повторение пройденного материала и подготовка к ГИА.
Участники: учащиеся 9-го класса с углублённым уровнем подготовки по алгебре.
Методика проведения урока. Урок проводится в форме игры, которая называется «Математический детектив». Учащиеся являются «полицейскими детективами». Они должны работать либо самостоятельно, либо в парах. Учитель объявляет, что пропало знаменитое высказывание Леонардо да Винчи. Задача детективов найти его. Проходя через определённые этапы, для учащихся будут открываться части пропавшего высказывания, но не по порядку. А в конце урока они должны составить из этих частей фразу. Лучшие детективы зачисляются в «Полицейскую академию», т.е. получают хорошие отметки. Данная форма урока выбрана неслучайно, т.к. именно игра позволяет повысить интерес к обучению. Задания, предлагаемые на уроке, позволяют вспомнить и повторить учебный материал по теме «Уравнения и неравенства» с 7-го класса по 9-й, также задания имеют разные уровни сложности (базовый и повышенный).
Урок носит интегрированный характер. Кроме предметной составляющей, он содержит исторические факты и погружает учащихся в среду детектива.
К методической разработке прилагается CD с электронными материалами: электронная версия методической разработки, презентация для проведения урока, приложение.
Оборудование
-
Компьютер учителя;
-
Мультимедийный проектор;
-
Интерактивная доска (или экран);
-
Презентация для проведения урока;
-
Листы А4 с высказыванием Леонардо Да Винчи, разбитым на части: «Ни одно», «человеческое исследование», «не может назваться истинной наукой», «если оно не прошло через», «математические доказательства» (см. Приложение);
-
Магниты для крепления листов на магнитную доску.
-
Небольшие листы бумаги для проведения этапа рефлексии.
Методические советы на подготовительный период
-
Данный урок является итоговым повторением темы «Уравнения и неравенства». Поэтому перед его проведением рекомендуется в течение трёх – четырёх уроков повторить:
-
Правила преобразования буквенных выражений [1];
-
Графический метод решения линейных уравнений [1] и квадратных неравенств [3], систем уравнений [5];
-
Основные формулы для решения квадратных уравнений и неравенств [5];
-
Метод интервалов для решения рациональных неравенств, в том числе с кратными корнями [5];
-
Приёмы преобразования иррациональных чисел [5];
-
Методы решения простейших неравенств с модулем [3];
-
Определение геометрической вероятности [5].
-
Обязательно оказать помощь слабым учащимся (предложить нужную книгу, указать страницу с необходимой информацией; назначить, если потребуется, консультанта по решению типовых задач ГИА по данной теме);
-
Подготовить необходимое оборудование (см. выше).
Ход урока-игры «Математический детектив»
На уроке используется мультимедийная презентация 9-Математический детектив.ppt
Сценарий урока-игры «Математический детектив»
Используется мультимедийная презентация 9-Математический детектив.ppt
-
(Слайд №1, 1 мин). Вступительное слово учителя: Сегодня урок повторения. Он пройдёт в форме игры, которая называется «Математический детектив». Вы – детективы. Работать будете самостоятельно и в парах. Пропало знаменитое высказывание Леонардо да Винчи. Ваша задача найти его. Проходя через определённые этапы, вам будут открываться части пропавшего высказывания. И в конце урока вы должны составить из этих частей фразу. Лучшие детективы будут зачислены в «Полицейскую академию». Начнём с теста на профессиональную пригодность.
-
Тест на профпригодность. (Проверяется базовый уровень знаний учащихся, учащиеся могут советоваться друг с другом, работать в паре).
-
(Слайд №2, 1 мин.) Выразить переменную1 t из формулы
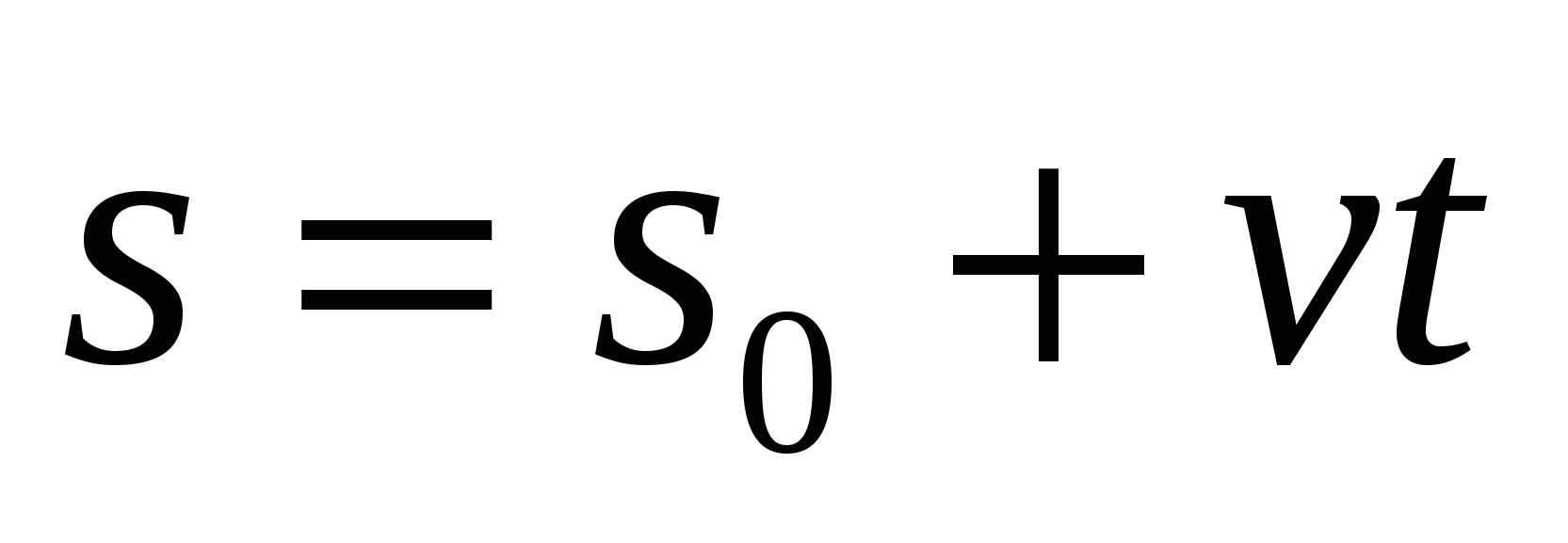 ;
;
(Правильный ответ слайд №3); -
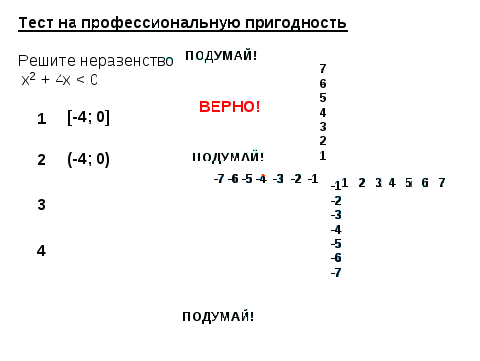
(Слайд №4, 1 мин). Решить неравенство2:
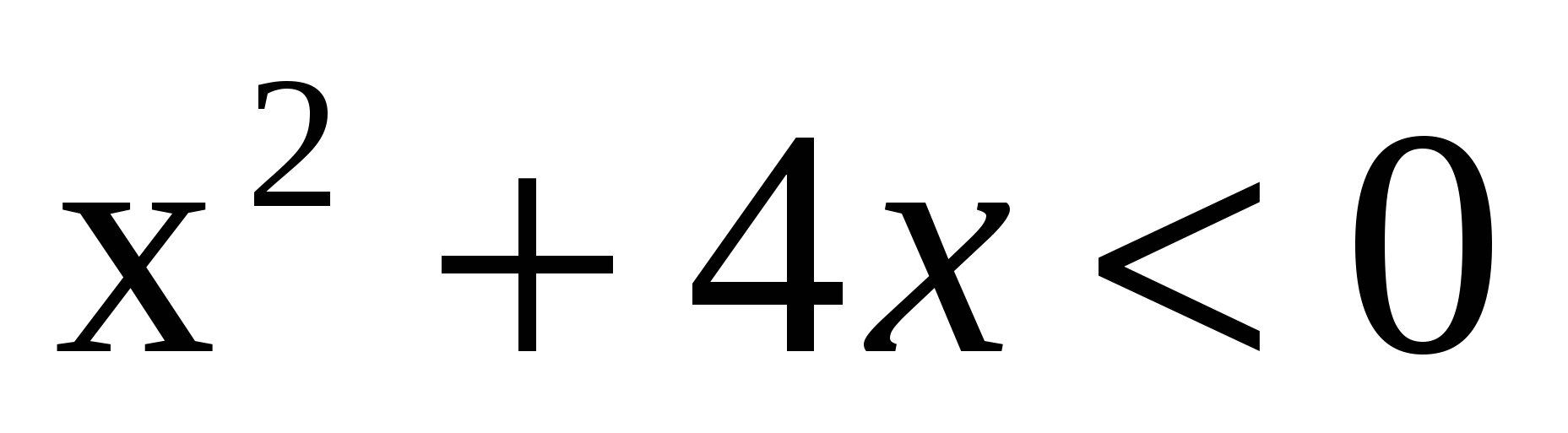 по предложенному графику, из четырёх вариантов ответов выбрать верный и прокомментировать. (Правильный ответ №2)
по предложенному графику, из четырёх вариантов ответов выбрать верный и прокомментировать. (Правильный ответ №2) -
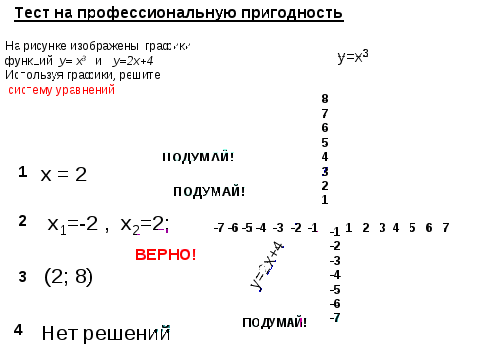
(Слайд №5, 1 мин). Решить систему уравнений3:
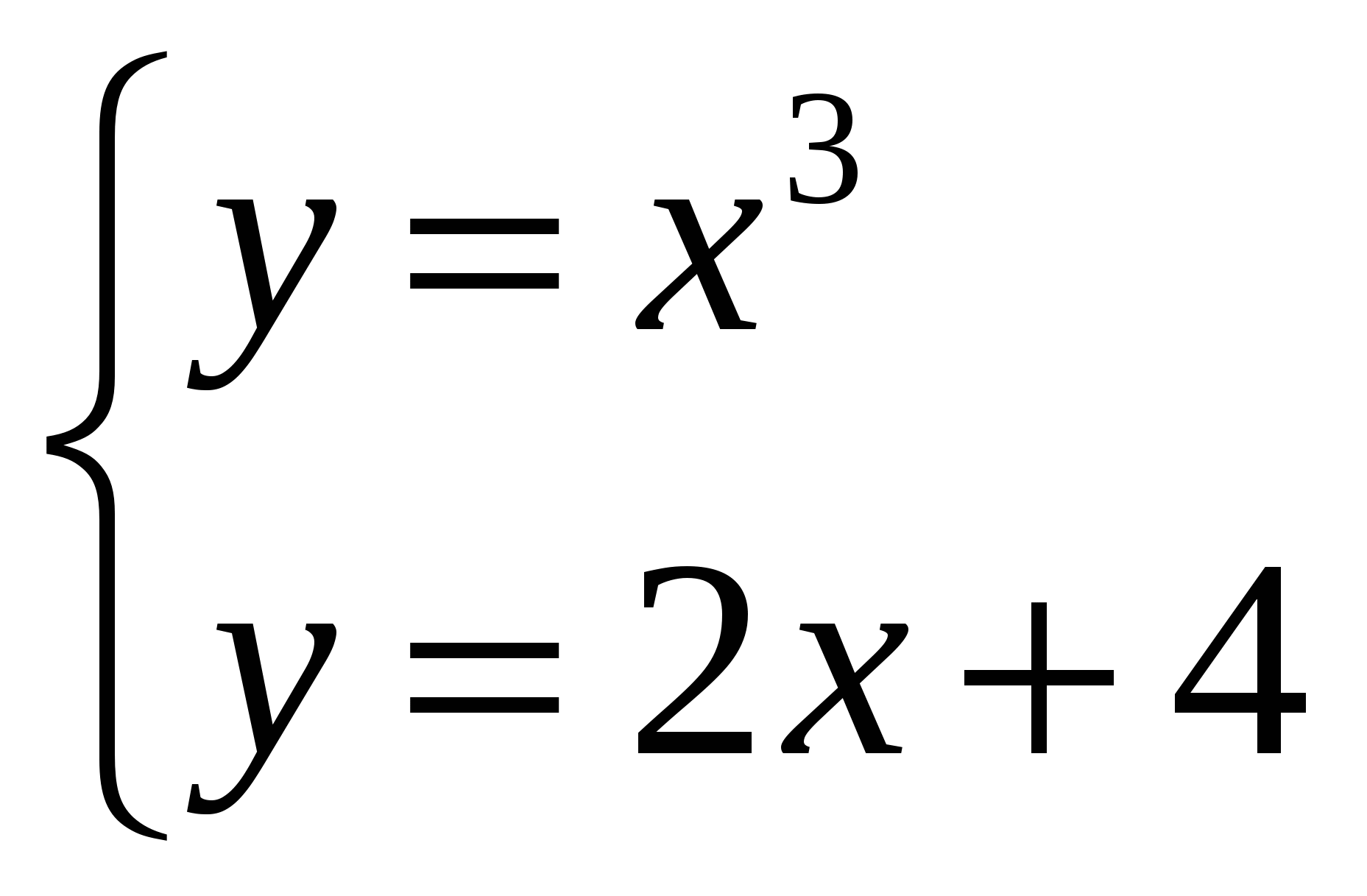 графическим методом (графики на слайде), из предложенных вариантов ответов выбрать верный и прокомментировать. (Правильный ответ №3)
графическим методом (графики на слайде), из предложенных вариантов ответов выбрать верный и прокомментировать. (Правильный ответ №3) -
(Слайд №6, 2 мин). Расположить в порядке возрастания числа4:
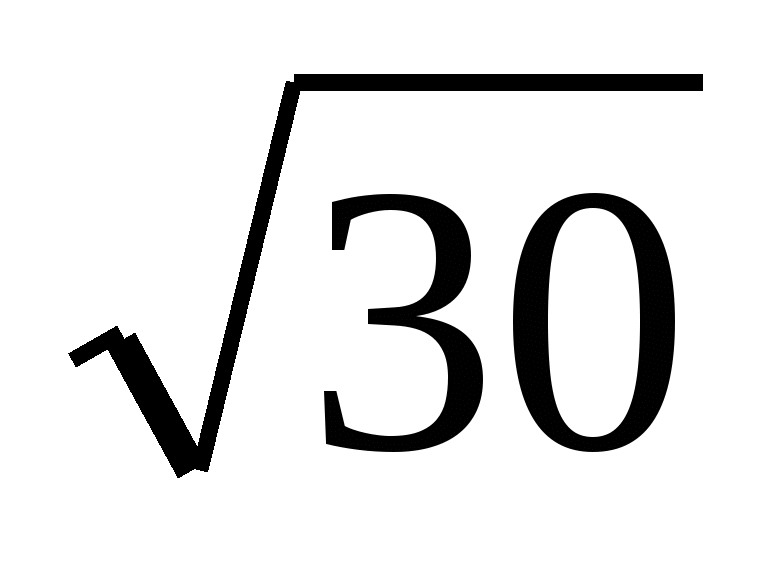 ;
; 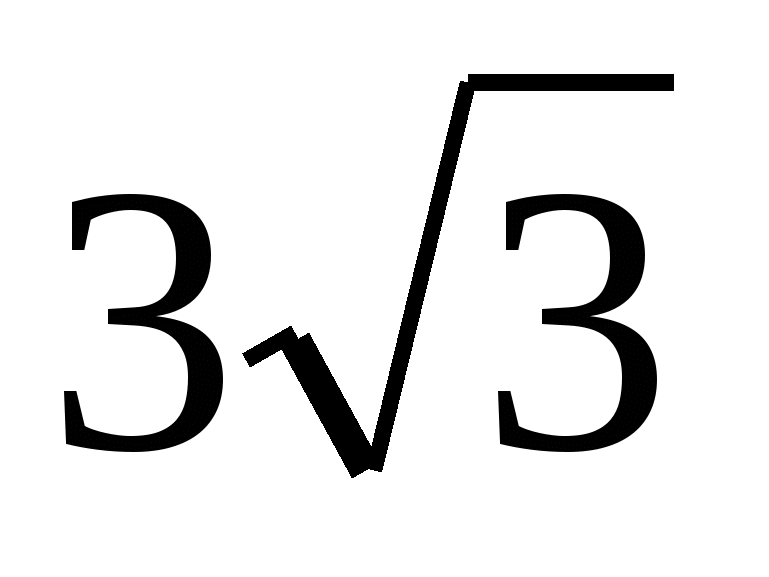 ; 5,5; ответ обосновать. (Правильный ответ:
; 5,5; ответ обосновать. (Правильный ответ: 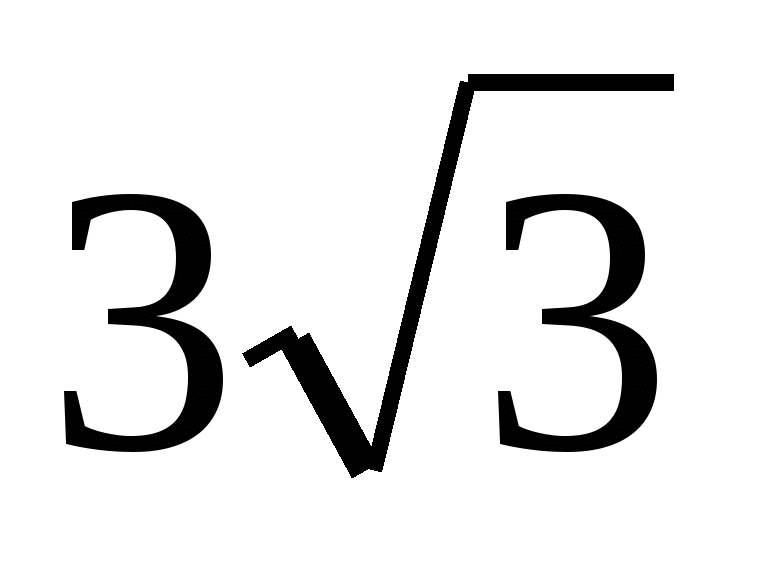 ;
;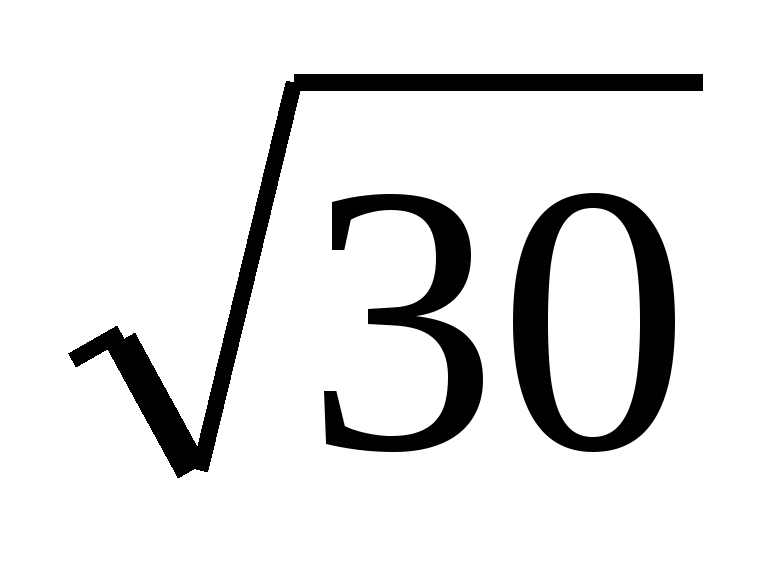 , 5,5).
, 5,5).
Учитель открывает часть фразы «математические доказательства.»
-
(Слайд №7) Опознание улик начнём со следственного эксперимента.
-
(Слайд №8, 2 мин). Задание по готовому чертежу (базовый уровень). Укажите рисунок, на котором приведена графическая иллюстрация решения системы линейных уравнений5:
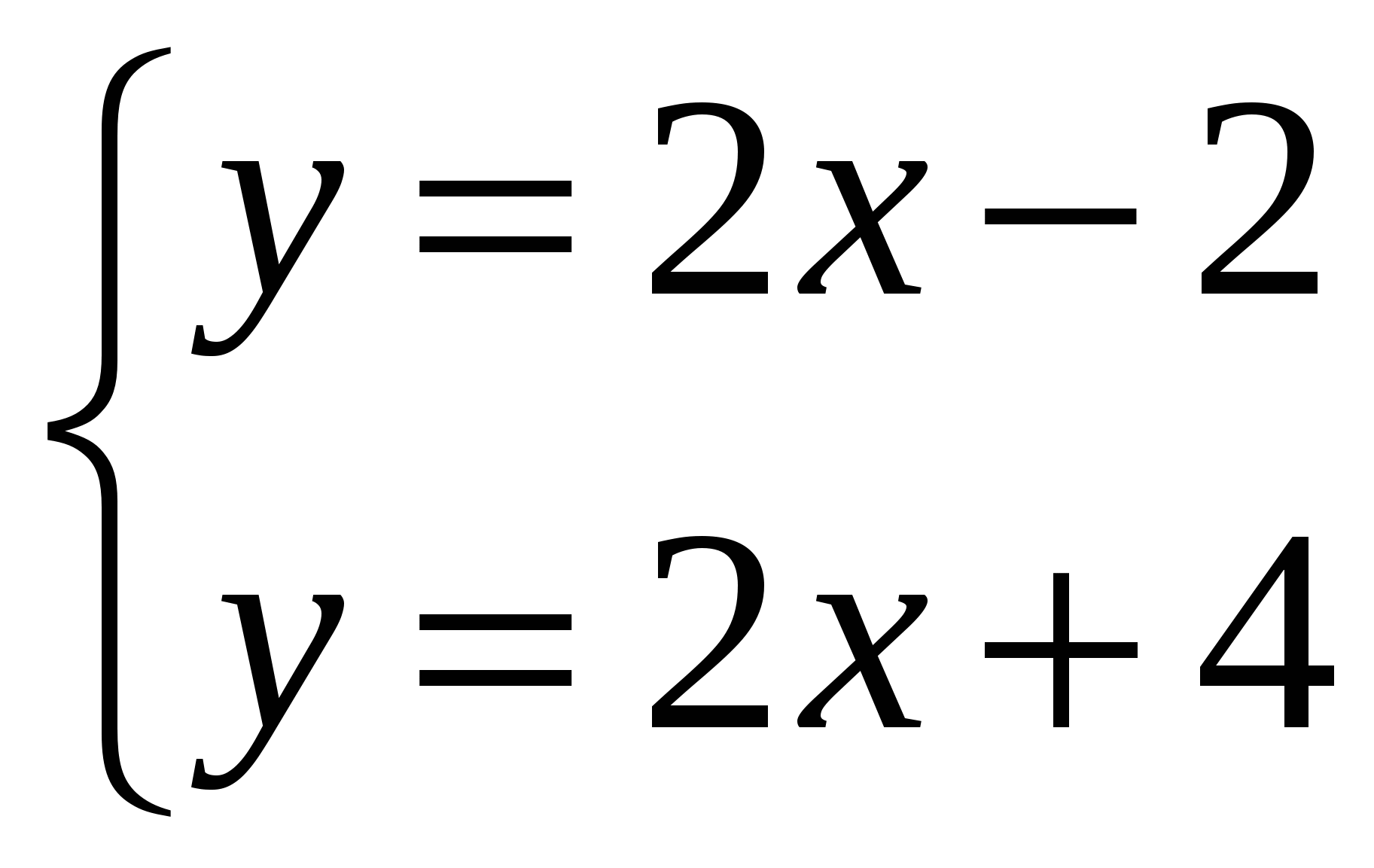 и прокомментируйте свой ответ. (Правильный ответ №3)
и прокомментируйте свой ответ. (Правильный ответ №3)
Учитель открывает часть фразы «если оно не прошло через».
-
(Слайд №9, 8 мин). Задание с параметром (повышенный уровень) 6: при каких значениях k число 0 находится между корнями уравнения
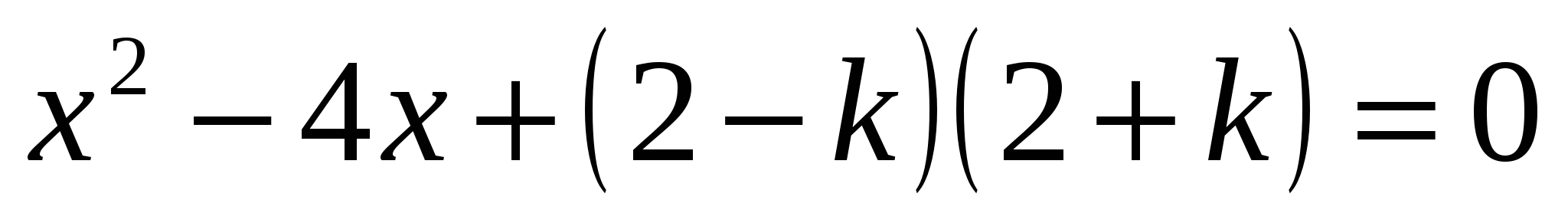 . (Правильный ответ и решение см. слайд №10).
. (Правильный ответ и решение см. слайд №10).
Учитель открывает часть фразы «Ни одно»
-
(Слайд №11, 5 мин). Опознание улик продолжим с помощью Фоторобота. (Повышенный уровень). Решить неравенство7 с кратными корнями
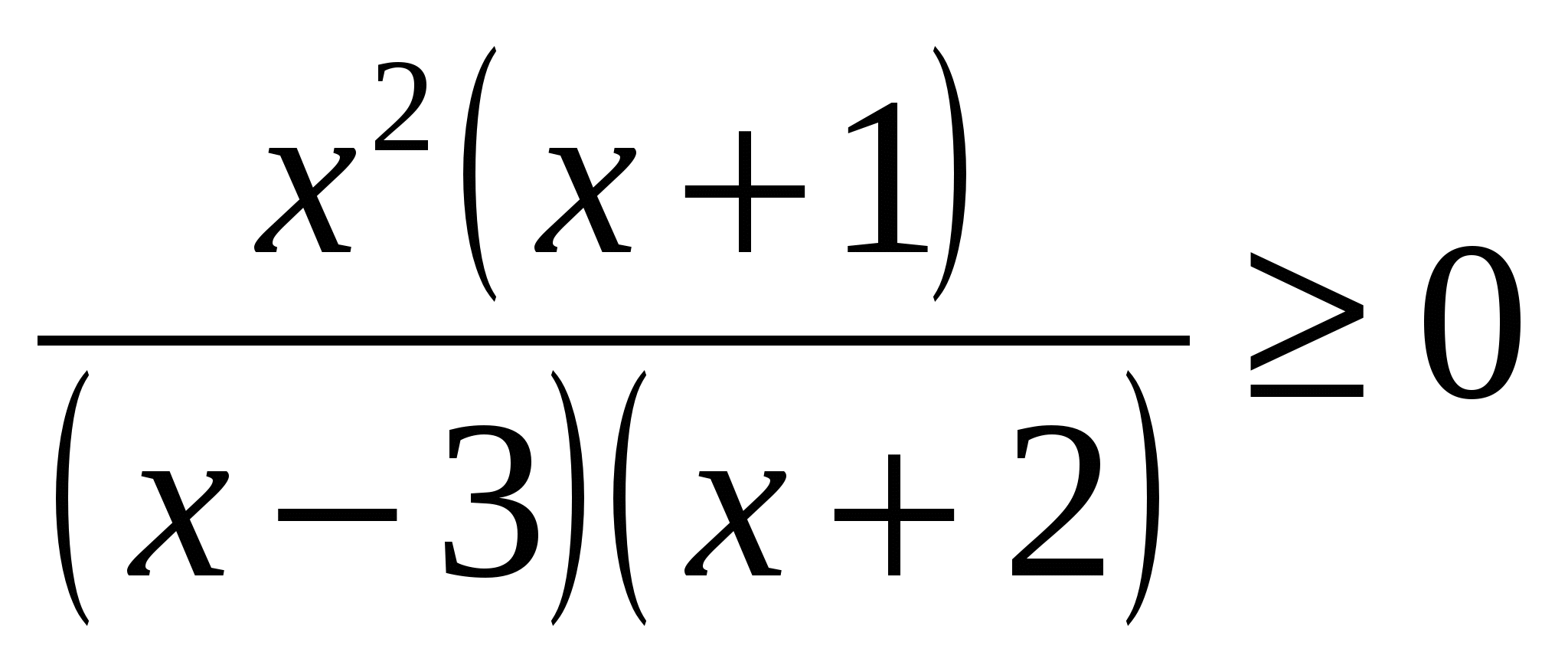 методом интервалов. (Правильный ответ:
методом интервалов. (Правильный ответ: 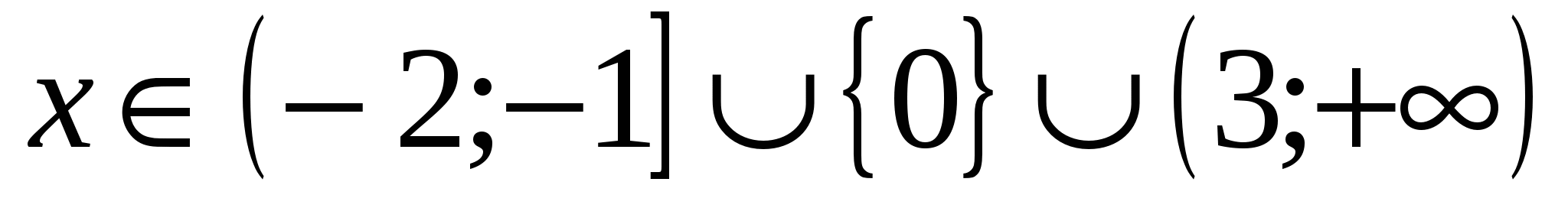 ).
).
Учитель открывает часть фразы «не может назваться»
-
(Слайд №12). А сейчас идём на детектор лжи (базовый и повышенный уровни).
Учитель: Перед вами появятся 5 математических высказываний. Если с ним вы согласны (т.е. ваш ответ «ДА»), то на листе бумаги маркерами вы рисуете  ; если вы не согласны с тем, что видите на доске, тогда ваш ответ «НЕТ» и вы рисуете на листе __. В результате должна появиться некоторая ломаная линия, которая покажет уровень ваших знаний.
; если вы не согласны с тем, что видите на доске, тогда ваш ответ «НЕТ» и вы рисуете на листе __. В результате должна появиться некоторая ломаная линия, которая покажет уровень ваших знаний.
(Слайды №13-17, 8 мин). Учащиеся пишут графический диктант:
Проверка проходит с помощью последующих слайдов презентации (Слайды №18-28, 2 мин). Верные утверждения учащиеся обосновывают, неверные – исправляют. (Правильный ответ: __ __ __
__ __ ).
).
Учитель: Поднимите руки те, у кого ломаная линия точно такая же.
Учитель открывает часть фразы «человеческое исследование».
-
(Слайд №29, 9 мин). Запутанный след
Задача на геометрическую вероятность8 (повышенный уровень). Случайным образом выбирают одно из решений неравенства 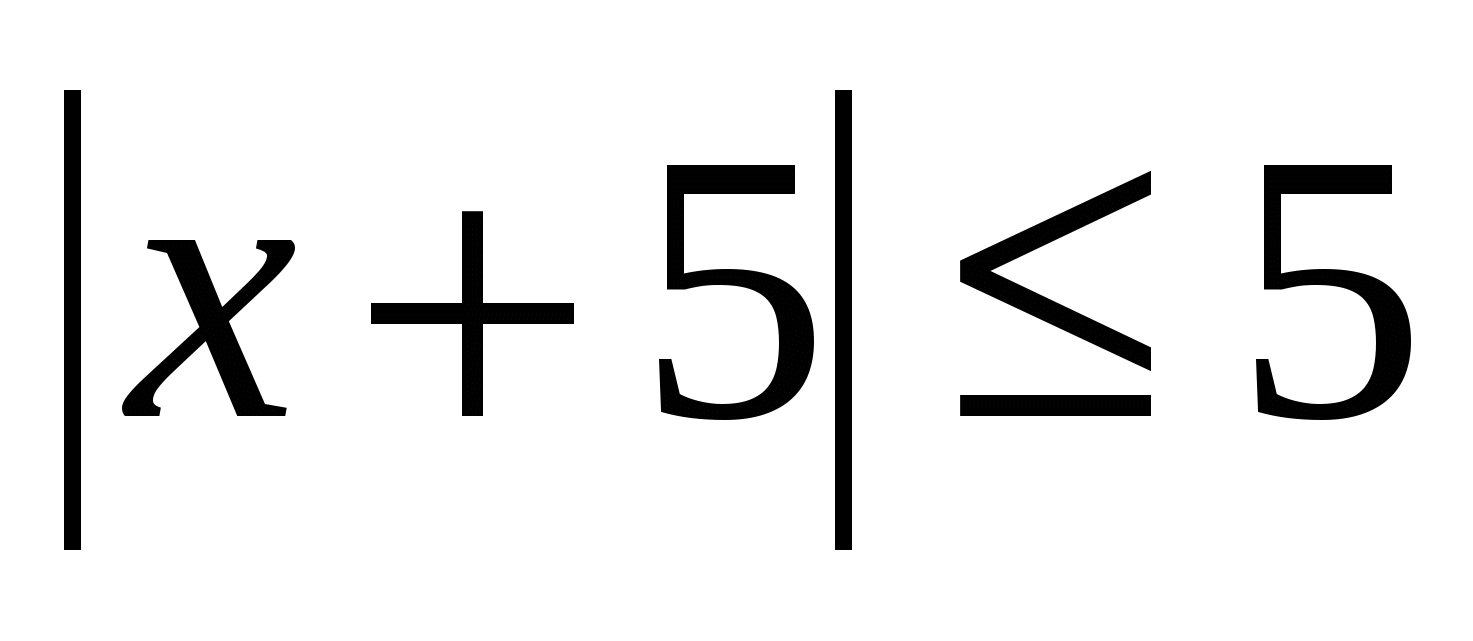 . Какова вероятность, что оно окажется и решением неравенства
. Какова вероятность, что оно окажется и решением неравенства 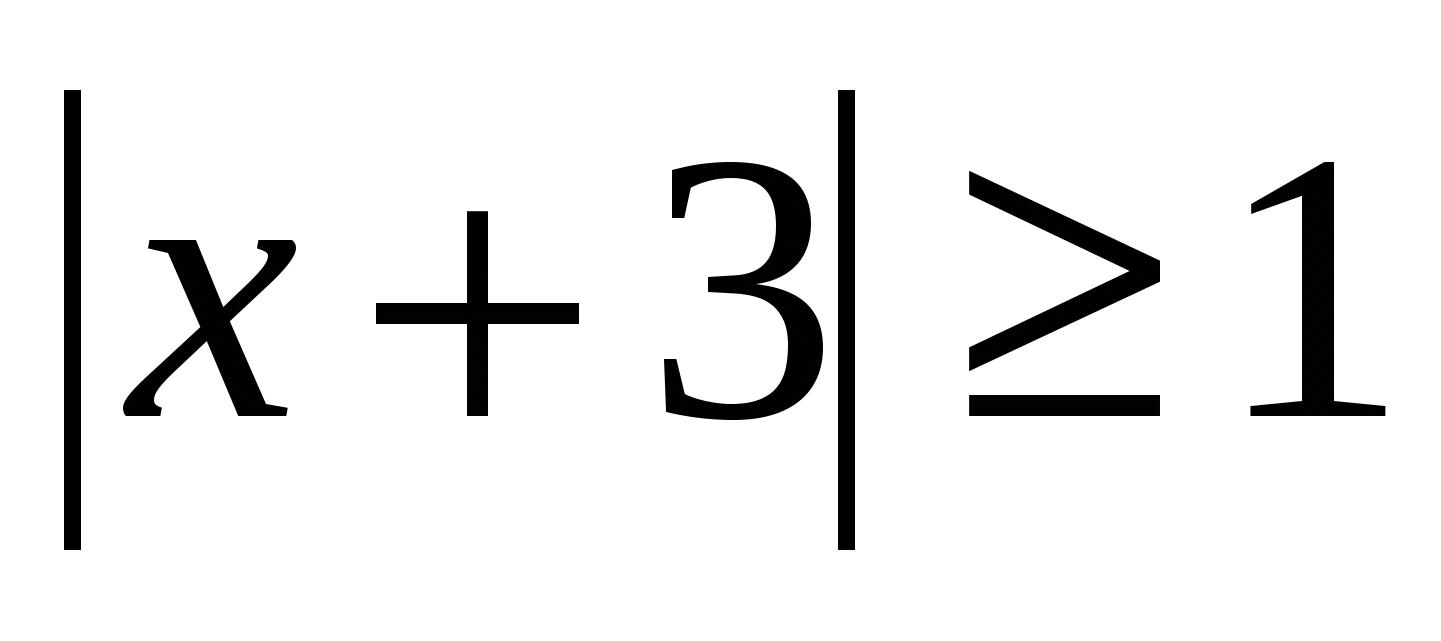 ? (Правильный ответ: р=0,8).
? (Правильный ответ: р=0,8).
Учитель открывает часть фразы «истинной наукой,».
-
(Слайд №30-31, 4 мин). Подведение итогов
Учитель: А теперь, детективы, соберите из частей знаменитое высказывание Леонардо да Винчи. (Правильный ответ: «Ни одно человеческое исследование не может назваться истинной наукой, если оно не прошло через математические доказательства»).
Учитель: Историческая справка о личности ЛЕОНАРДО ДА ВИНЧИ. Годы жизни: 1452-1519. Леонардо Да Винчи – итальянский живописец, скульптор, архитектор, ученый, инженер. Родился в семье богатого нотариуса. Если в молодости он преимущественное внимание уделял живописи, то с течением времени это соотношение изменилось в пользу науки. Трудно найти такие области знания и техники, которые не были бы обогащены его крупными открытиями и смелыми идеями.
Как ученый и инженер Леонардо да Винчи обогатил почти все области знания того времени. Особое внимание Леонардо уделял механике, называя ее “раем математических наук”. Видя в ней ключ к тайнам мироздания, он попытался определить коэффициенты трения скольжения, изучал сопротивление материалов, увлеченно занимался гидравликой. Многочисленные гидротехнические эксперименты получили выражение в новаторских проектах каналов и ирригационных систем.
Страсть к моделированию приводила Леонардо к поразительным техническим предвидениям, намного опережавшим эпоху: таковы наброски проектов металлургических печей и прокатных станов, ткацких станков, печатных, деревообрабатывающих и прочих машин, подводной лодки и танка.
Неутомимый ученый-экспериментатор и гениальный художник, Леонардо да Винчи стал общепризнанным символом эпохи Возрождения.
Итак, сегодня, играя, мы повторили тему: «Уравнения и неравенства». Лучшими детективами признаны… Они будут приняты в «Полицейскую академию».
-
(Слайд №32, 1 мин). Домашнее задание: текстовая задача на движение №14.01 [6] .
Рефлексия реализуется на заранее приготовленных небольших листочках бумаги с помощью специальных символов: «Улыбка», «Равнодушие», «Огорчение». Учащиеся выражают свое отношение к проведенному уроку LKJ. А также им предлагается закончить предложения:
-
«Сегодня на уроке…»;
-
«Хочется пожелать, чтобы…» .
-
(Слайд №33) Всем спасибо.
Методические советы организаторам
-
Урок проводите в конце учебного года, когда начинается подготовка к ГИА.
-
Эмоциональный настрой создаётся благодаря игровой форме урока и мультимедийной презентации. Идея проведения урока в форме математического детектива хорошо подходит психологически возрасту учащихся 9-го класса и вызывает интерес.
-
С тестом на профпригодность рекомендуется работать фронтально. При этом обратите внимание на то, как учащиеся аргументируют свои ответы, на точность данных ими формулировок, грамотность использования математической символики и речи. Перед ответом дайте немного времени на самостоятельное обдумывание или запись решения. Возможно, чтобы дети работали в паре. Те же рекомендации относятся и к первому следственному эксперименту (задание базового уровня). Во время опроса лучше дайте возможность отвечать учащимся среднего и низкого уровней подготовки.
-
Для решения задач второго следственного эксперимента и опознания улик с помощью фоторобота (задания повышенного уровня) рекомендуется вызывать к доске учащихся с высоким или средним уровнем подготовки. Остальные работают в тетрадях.
-
На детекторе лжи учащиеся пишут графический диктант. Возможно, чтобы дети работали в паре, советуясь и помогая друг другу. Во время проверки дайте возможность учащимся аргументировать свои ответы. Отвечать могут все желающие.
-
Для экономии времени урока при решении задачи на геометрическую вероятность, связанную с решением двух неравенств с модулем, рекомендуется вызвать к доске двух учащихся одновременно, распределив между ними эти неравенства.
-
Угадывание знаменитого высказывания Леонардо Да Винчи обычно не вызывает больших затруднений, поэтому дайте возможность ответить слабому учащемуся.
-
Для проведения рефлексии заранее приготовьте небольшие листочки бумаги и раздайте на парты перед уроком.
-
В конце урока не забудьте обязательно отметить ответы выступающих, объявить оценки, поблагодарить за урок.
Методические советы на период ближайшего последствия
Данные советы зависят от того, как учащиеся будут справляться с предложенными заданиями. Вы, как учитель увидите, что, возможно, требует дополнительного обсуждения. Но, как показывает практика, если предварительное повторение было построено на должном уровне, то учащиеся будут успешно справляться с предложенными заданиями.
Список литературы
-
Учебный комплект из двух книг для классов с повышенным уровнем изучения алгебры в 7 классе:
-
Алгебра. 7 класс. В 2-х ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, Н.П. Николаев. – М.: Мнемозина, 2009;
-
Алгебра. 7 класс. В 2-х ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович, Н.П. Николаев. – М.: Мнемозина, 2009;
-
Учебный комплект из двух книг для углублённого изучения алгебры в 8 классе:
-
Алгебра. 8 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, Н.П. Николаев. – 4-е изд., перераб. – М.: Мнемозина, 2008. (Учебник для классов с повышенным уровнем математической подготовки в общеобразовательных школах).
-
Алгебра. 8 класс: задачник для учащихся общеобразовательных учреждений / Л.И. Звавич, А.Р. Рязановский. – 5-е изд., перераб. – М.: Мнемозина, 2008;
-
Учебный комплект из двух книг для углублённого изучения алгебры в 9 классе:
-
Алгебра. 9 класс. В 2-х ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, Н.П. Николаев. – 4-е изд., стер. – М.: Мнемозина, 2009;
-
Алгебра. 9 класс. В 2-х ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / Л.И. Звавич, А.Р. Рязановский, П.В. Семёнов. – 4-е изд., испр. – М.: Мнемозина, 2009;
-
Алгебра: сб. заданий для подготовки к гос. итоговой аттестации в 9 кл. /[Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др.]. – 5-е изд. – М.: Просвещение, 2010.
Автор методической разработки: Жилякова Ольга Владимировна,
учитель математики МБОУ СОШ №24 Асбестовский городской округ.
1 Задание №2 (Вариант 2, Работа №4) [7]
2 Типовое задание №13 и №15 [7]
3 Типовое задание №10 [7]
4 Задание №3 (Вариант 1, Работа №10) [7]
5 Типовое задание №9.69 [2]
6 Типовое задание №39.48 [4]
7 Задание №1.13(б) [6]
8 Задание №28.24(б) [6]