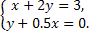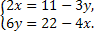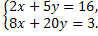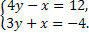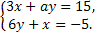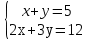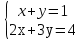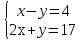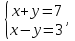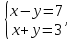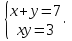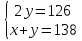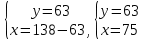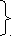ТЕМА УРОКА: Метод алгебраического сложения.
| Девиз урока: «Деятельность — единственный путь к знанию» Дж.Бернард Шоу
|
Основная цель: Сформировать умение решать системы двух линейных уравнений с двумя переменными способом алгебраического сложения.
ЦЕЛИ УРОКА:
-
Формирование способности к самостоятельному исследованию системы линейных уравнений с двумя переменными.
-
Развитие способности к самостоятельному планированию, организации работы; развитие умений находить и использовать необходимую информацию в сети Интернет.
-
Воспитание познавательного интереса к математике и информатике.
-
Развитие информационных компетенций учащихся.
Задачи урока
– обучающие ( формирование познавательных УУД):
-
показать метод решения,
-
формировать умение решать системы уравнений методом сложения.
-развивающие ( формирование регулятивных УУД):
-
развитие познавательных интересов,
-
умение получения новой информации, используя репродуктивную технологию учения;
-
развитие у учащихся аналитических умений средствами информационных технологий
-воспитательные ( формирование коммуникативных и личностных УУД):
-
воспитание навыков контроля и самоконтроля,
-
развитие коммуникативных навыков при работе в группах.
План урока:
1. Организационный момент.
2. Проверка домашнего задания.
3. Устный счет.
4. Закрепление изученного материала.
5.Обучающая самостоятельная работа.
6.Подведение итогов урока, постановка домашнего задания.
Ход урока:
I. Организационный момент. (Сообщение цели и плана урока учащимся.)
Уважаемые учащиеся!
Сегодня на уроке вам предстоит познакомиться с графическим решением системы линейных уравнений с двумя переменными, а также научиться самостоятельно исследовать системы линейных уравнений с двумя переменными на наличие решений. А сначала, давайте повторим основные факты и определения предыдущих уроков, которые помогут вам в освоении нового материала.
-
Проверка домашнего задания (выборочно, если есть вопросы учащихся).
-
Актуализация опорных знаний.
Устный математический диктант.
Закончите предложения:
1.Линейным уравнением с двумя переменными называется…
2.Решением линейного уравнения с двумя переменными называется…
3.Решением системы двух линейных уравнений с двумя переменными называется…
4.Решить систему линейных уравнений с двумя переменными называется…
5.Какие способы решения системы линейных уравнений с двумя переменными вам известны?
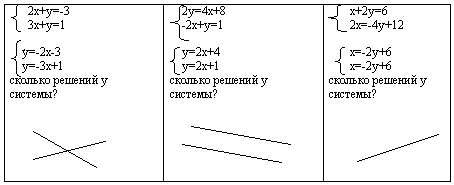
6.Не выполняя построения, определите, как расположены графики уравнений системы и сделайте вывод относительно числа ее решений.
| Б | В | Г | |
|
|
|
|
|
7.Существует ли такое значение a, при котором система
а) имеет бесконечно много решений;
б) не имеет решений.
8. Решение «одним взглядом».
Вывод: система линейных уравнений может иметь одно решение, не иметь решений, иметь множество решений.
Исторические сведения Шилова Арина 1 минута
Возможность формулировать одни и те же утверждения и на геометрическом, и на алгебраическом языке дает нам система координат, изобретение которой, как вы уже знаете, принадлежит Рене Декарту — французскому философу, математику и физику. Именно он создал основы аналитической геометрии, ввел понятие геометрической величины, разработал систему координат, осуществил связь алгебры с геометрией.
9. Задания с опережением.
Запишите с помощью систем уравнений следующие ситуации:
-
Сумма двух чисел равна 17. Одно число на 7 меньше другого.
-
В классе 26 учеников. Девочек на 3 меньше, чем мальчиков.
-
Периметр прямоугольника равен 400м. Его дина в 3 раза больше ширины.
-
У мальчика было 14 монет по пять и десять рублей, всего на сумму 115 рублей.
-
Поезд прошел первый перегон за 2 часа, а второй за 3 часа. Всего за это время он прошел 330 километров, причем скорость на втором перегоне была на 10 км/ч была больше, чем на первом.
| V, км/ч | t, ч | S, км |
|
| I перегон | х | 2 |
|
| II перегон | у | 3 |
|
Тест
1) Решением какой системы уравнений является пара чисел (-1;2)?
а) 
б) 
в) 
2) В уравнении 2х + у = 8 выразите х через у:
а) х = 4 +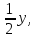 
б) х = 8 – 2у, в)х = 4 —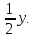 
3) Сумма двух чисел равна 7, а их разность 3. С помощью какой из систем можно решить эту задачу?
а) 
б) 
в) 
4) Дана система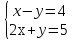 
. Какая из пар чисел является её решением?
а) (4;0), б) (3;0), в)(3; -1).
5) Сколько решений имеет система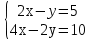 
?
а) одно, б) бесконечно много, в) не имеет решений.
Ответы: 1.б; 2.в; 3.a; 4.в; 5. б.
Проверка осуществляется взаимообменом работ с соседом по парте.
Критерии оценивания:
| Отметка | |
| 5 заданий | 5 |
| 4 задания | 4 |
| 3 задания | 3 |
| 1-2 задания | 2 |
-
Основная часть (Закрепление)
а) Задания №13.3-13.8 (б) — Коллективное решение у доски.
б) Решение на обратной стороне доски. 2 человека. Карточка — Индивидуально.
Решите систему уравнений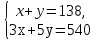 
методом алгебраического сложения.
Решите систему уравнений 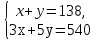методом подстановки.
в) Решение литературной задачи.
В известном рассказе А.П.Чехова «Репетитор» описана задача, которую можно решить с помощью систем уравнений. Герои рассказа — купец Удодов, его сын Петя — семиклассник и Петин репетитор, Зиберов Егор Александрович. Рассмотрим отрывок из этого рассказа. Итак, репетитор Зиберов диктует Пете задачу: «Купец купил 138 аршин черного и синего сукна за 540 рублей. Спрашивается, сколько аршин купил он того и другого, если синее сукно стоило 5 рублей за аршин, а черное — 3 рубля?»
Пусть х аршин купец купил черного сукна, а у аршин — синего сукна. Так как всего купец купил 138 аршин, то х + у =138. Синее сукно по 5 рублей, а черное — по 3 рубля, и всего он заплатил 540 рублей, то 3х + 5у = 540. Составляем систему уравнений: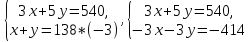 
, 
.
Ответ: купец купил 75 аршин черного сукна и 63 аршина синего сукна.
-
Обучающая самостоятельная работа (Блицопрос)
1вариант
1.Решите систему уравнений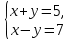 
методом алгебраического сложения.
Решение: _________________________________________________________________
_________________________________________________________________________
Ответ: ______________________________
2.Решите систему уравнений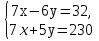 
методом алгебраического сложения.
Решение: _________________________________________________________________
_________________________________________________________________________
Ответ: ______________________________
2 вариант
1.Решите систему уравнений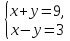 
методом алгебраического сложения.
Решение: _________________________________________________________________
_________________________________________________________________________
Ответ: ______________________________
2.Решите систему уравнений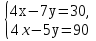 
методом алгебраического сложения.
Решение: _________________________________________________________________
_________________________________________________________________________
Ответ: ______________________________
Дополнительно Задание 13.12(б)
-
Подведение итогов урока. Рефлексия (вопросы).
-
Что нового вы узнали на уроке?
-
Что использовали для «открытия» нового знания?
-
Алгоритм решения системы двух линейных уравнений с двумя переменными способом алгебраического сложения:
1. Умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными.
2. Складывают почленно левые и правые части уравнений системы.
3. Решают получившееся уравнение с одной переменной.
4. Находят соответствующее значение второй переменной.
-
Проанализируйте свою работу на уроке.
-
Постановка домашнего задания
Повторить § 13. Решить задания №13.3-13.8 (в).
В качестве дополнительного задания вам предлагается подготовить сообщение и презентацию о жизни и деятельности Рене Декарта. Ваша презентация может содержать исторические сведения, научные факты. Вы можете посвятить ее какой-нибудь одной задаче или проблеме, связанной с Рене Декартом. Основное требование — ваше сообщение не должно превышать 10 мин. Срок выполнения данного задания — 1 неделя. Желаю успеха!
Критерии, по которым будет оцениваться презентация:
-
критерии к содержанию презентации (5-7 баллов);
-
критерии к дизайну презентации (5-7 баллов);
-
соблюдение авторских прав (2-3 балла)
Сведения о Рене Декарте можно найти здесь:
http://pikalova-ms.narod.ru/portrety_matemaikov.htm
http://refu.ru/refs/88/19707/1.html
http://ru.wikipedia.org/wiki/Декарт,_Рене
http://www.peoples.ru/science/mathematics/descartes/