СЛАГАЕМОЕ ПРЕКРАСНОГО.
Морина Светлана Алексеевна, учитель математики, МБОУ СОШ №5 города-курорта Железноводска Ставропольского края
Предмет (направленность): наглядная геометрия.
Возраст детей: 6 класс.
Место проведения: класс.
Тип урока: изучение нового материала.
Технические средства: мультимедийное оборудование, компьютеры, ноутбуки, планшеты,
Дидактические материалы: модели фигур (из цветной бумаги), раздаточный материал (приложение 2), карточки с буквами (приложение 3). (Раздаточный материал и карточки с буквами лежат на столах учеников в конвертах с надписями или скрепленные скребками.)
ЦОР:
— презентация в программе PowerPoint,
— видеоролик, созданный учеником, http://youtu.be/1lTRBnMyYnc
-видео ролик «Отзвуки вальса» (http://narod.ru/disk/64744485001.3b1812c8502c25f27f16039fa092f298 /Г.Свиридов%20-%20Отзвуки%20вальса.mp4.html ),
— программный комплекс «Наглядная геометрия» (Единая коллекция цифровых образовательных ресурсов. Программа «Орнаменты» http://school-collection.edu.ru/catalog/rubr/f9aff3d4-713b-4a6e-a064-24a0d8733e6d/104804/?interface=catalog&class=47&subject=18 ),
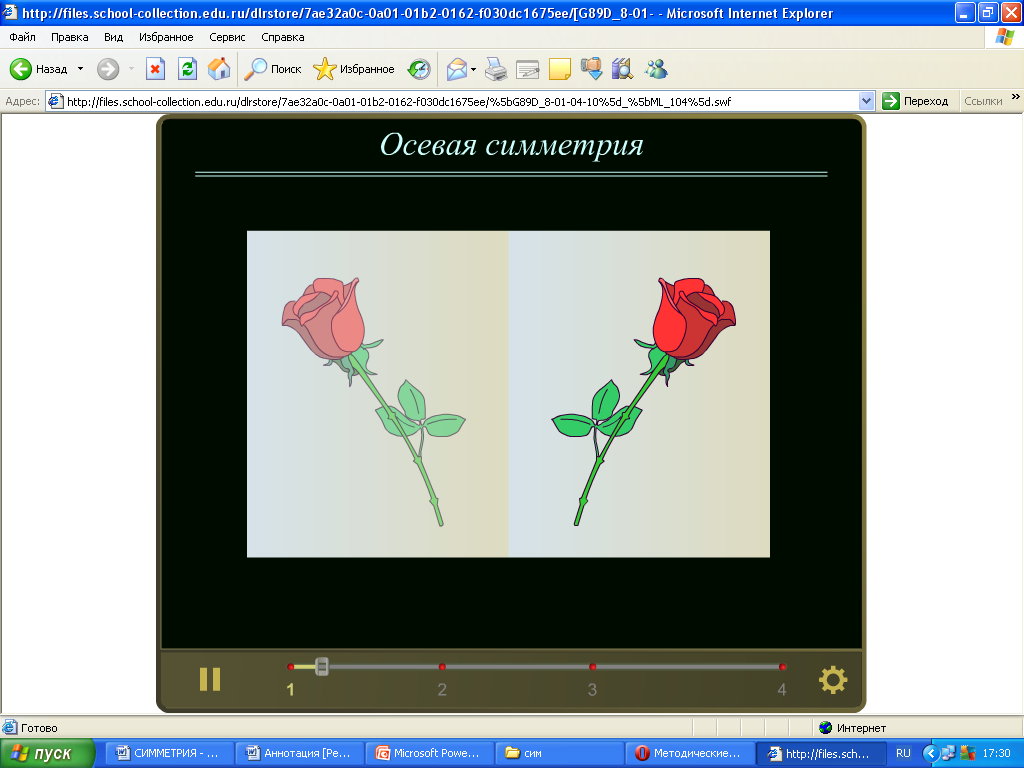
— ресурс «Осевая симметрия» из Единой коллекции цифровых образовательных ресурсов.
http://files.school collection.edu.ru/dlrstore/7ae32a0c-0a01-01b2-0162-f030dc1675ee/%5bG89D_8-01-04-10%5d_%5bML_104%5d.swf
Цели и задачи:
Цель урока: создание условий для формирования понятия симметрии (осевой), некоторых свойств геометрических фигур, построения симметричных фигур.
Задачи урока.
Образовательные:
отработка умений определять понятия осевой симметрии;
реализация задачи внутрипредметных и межпредметных связей с биологией, музыкой, архитектурой.
Воспитательные:
воспитание эстетического отношения к красоте теории, законов окружающего мира, умений ценить красоту собственного труда;
воспитание уважения друг к другу, взаимопонимания, уверенности в себе.
Развивающие:
развитие творческого, логического мышление ученика; углубление знания об окружающем мире путем творческих поисков; развитие потребности к самообразованию.
Ход урока.
-
Орг. момент.
-
Вхождение или погружение в тему.
Учитель: Опыты с зеркалами, проделанные на прошлом уроке, позволили нам прикоснуться к одному из удивительных математических явлений. Тема нашего сегодняшнего урока «Слагаемое прекрасного». О каком слагаемом пойдёт речь, вам предстоит узнать, разгадав кроссворд.(слайд 2).
Вопросы кроссворда.
1.Сумма этих углов равна 180 градусов.
2.Одно из средств изображения трехмерного пространства на плоскости.
3. Единица измерения длины.
4. Головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры.
5. Часть прямой.
6. Простейшая геометрическая фигура.
7. Правильный многогранник.
8. Замечательная кривая.
9. Геометрическая фигура.
3. Интерактивная лекция.
Учитель: Почему мы находим одни вещи красивыми, а другие нет? Почему некоторые люди кажутся нам более привлекательными, а другие менее? Кристи Тарлинктон – супермодель, признанная одной из самых красивых женщин в мире, — считает, что по большей части обязана своим успехом в качестве модели идеальной симметрии своих губ. Пропорция и симметрия объекта всегда необходимы нашему зрительному восприятию для того, чтобы мы могли считать этот объект красивым. Баланс и пропорция частей относительно целого обязательны для симметрии. Смотреть на симметричные изображения приятнее, нежели на асимметричные. В древности слово «симметрия» употреблялось в значении «гармония», «красота».
Эпиграфом нашего занятия я хочу предложить вам слова Платона: « Почти все утверждают, что красоту, воспринимаемую зрением, порождает соразмерность частей друг с другом и целым и с прелестью красок. И для тех, кто это утверждает, и вообще для всех остальных быть прекрасным — значит быть симметричным и соразмерным».(слайд 3).
Посмотрите на кленовый лист, снежинку, бабочку. Их объединяет то, что они симметричны. Если поставить зеркальце вдоль прочерченной на каждом рисунке прямой, то отраженная в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура). Поэтому такая симметрия называется зеркальной или осевой (если речь идет о плоскости). (слайд 4). Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Давайте рассмотрим строгое определение осевой симметрии.
(Просмотр ЦОР из коллекции по ссылке http://files.school-collection.edu.ru/dlrstore/7ae32a0c-0a01-01b2-0162-f030dc1675ee/%5bG89D_8-01-04-10%5d_%5bML_104%5d.swf просмотреть только 1 пункт ресурса. На загрузку ресурса уходит примерно 1 минута. С целью экономии времени можно открыть ресурс заранее, и запустить когда необходимо, то есть не осуществлять переход по ссылке со слайда презентации) – фронтальная работа с ресурсом.
Учитель: Если симметричную фигуру сложить вдоль оси симметрии, то её части совпадут. (Учитель демонстрирует данное свойство на модели прямоугольника, вырезанного из цветной бумаги). Возьмите в руки модель равнобедренного треугольника и найдите «перегибанием» ось симметрии. (Учащиеся находят ось симметрии на модели).
— Практическое задание (приложение 2). Слайд 5. Среди фигур выберете симметричные и проведите в них всевозможные оси симметрии. (Так же у учащихся на столах имеются модели данных фигур, вырезанные из цветной бумаги. Данные модели учащиеся могут использовать для нахождения осей симметрии, путем перегибания. Ученик может не использовать модели, а построить оси, путем воображения. Проверка после выполнения задания.
Учитель: Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность. Я хочу вам предложить посмотреть фильм о симметрии в архитектуре, созданный в прошлом учебном году учеником 6 «б» класса Лямзиным Олегом. (Просмотр фильма. Слайд 6).
— Просмотр видеофильма.
4.Эмоциональная разрядка.
Провести динамическую паузу.
Пальчиковая игра с математическим содержанием. (выполняется стоя). http://mdou7.caduk.ru/p87aa1.html
— Вот дом под треугольной крышей, который построил Джек (складывают руки над головой в виде треугольника).
— А это, круглое солнце, которое светит над домом, который построил Джек (складывают кисти рук над головой в виде круга).
— А это, квадратные окна в доме, который построил Джек.
— А это, высокие и низкие ступени в доме, который построил Джек (шагаем высоко и низко поднимая ноги).
— А это, длинная река, текущая у дома с треугольной крышей, над которой светит круглое солнце у дома, который построил Джек.
— А это, широкая и узкая дорожка, ведущие к дому с треугольной крышей, который построил Джек (развести руки в стороны поднять вверх).
— А это, высокое небо над домом с треугольной крышей, который построил Джек (тянутся).
— А это, прыгают лягушки у дома с треугольной крышей, квадратными окнами, высокими и низкими ступеньками, который построил Джек.
— А это, веселые люди, живущие в доме с треугольной крышей, (дети улыбаются) квадратными окнами, высокими и низкими ступенями, широкой и узкой дорожкой, ведущей к дому, который построил Джек.
5. Проработка содержания темы.
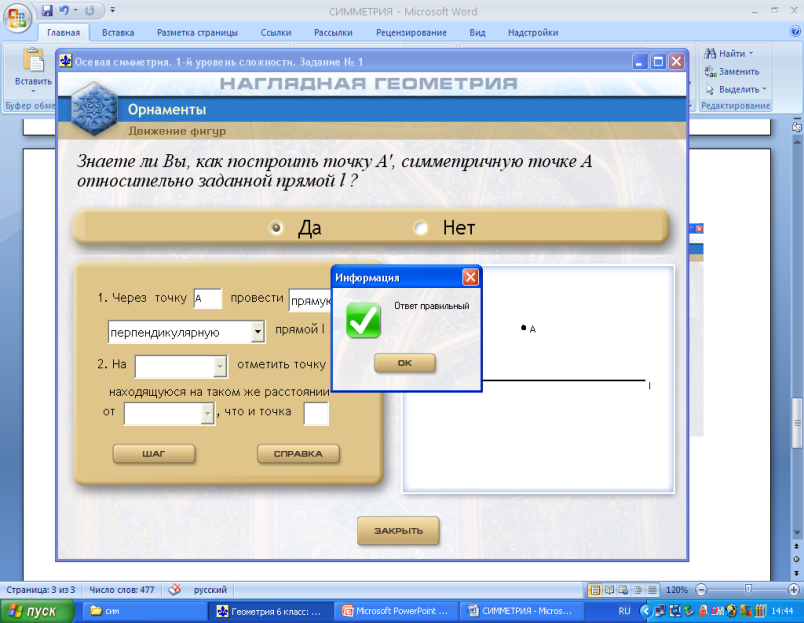
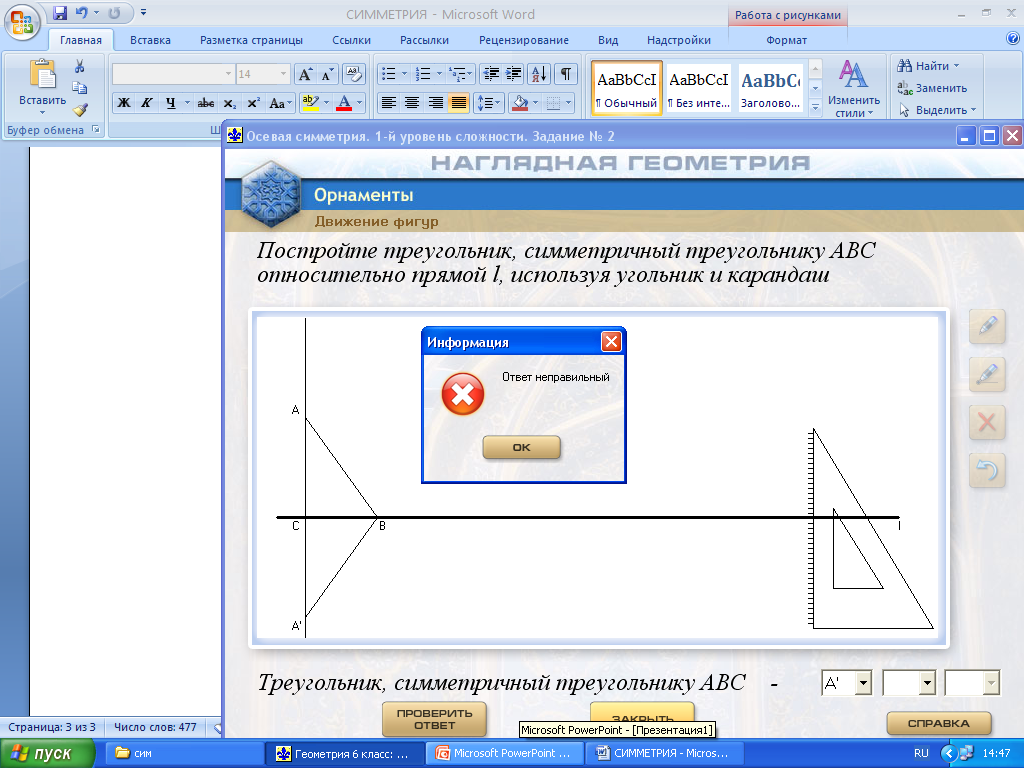
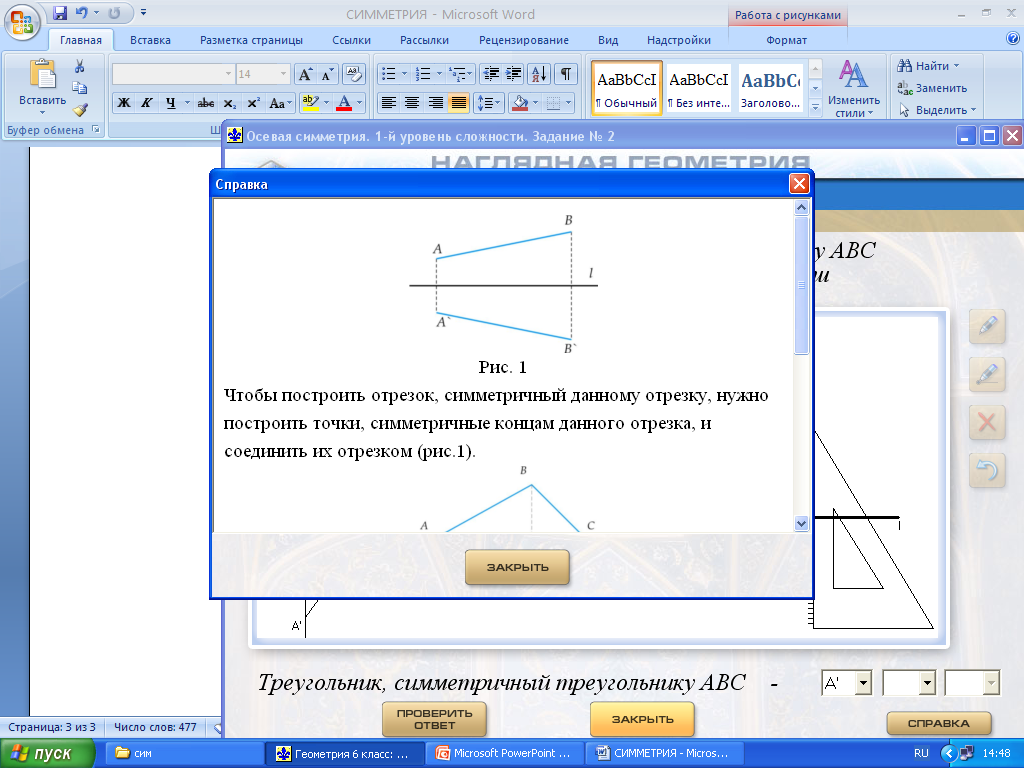
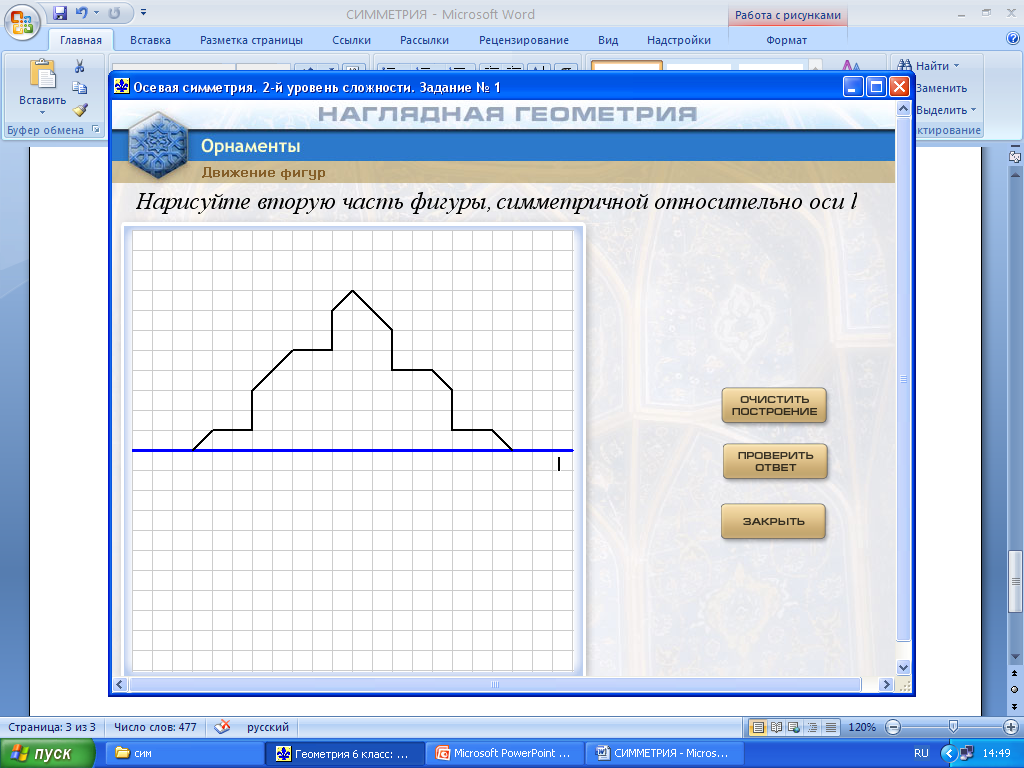
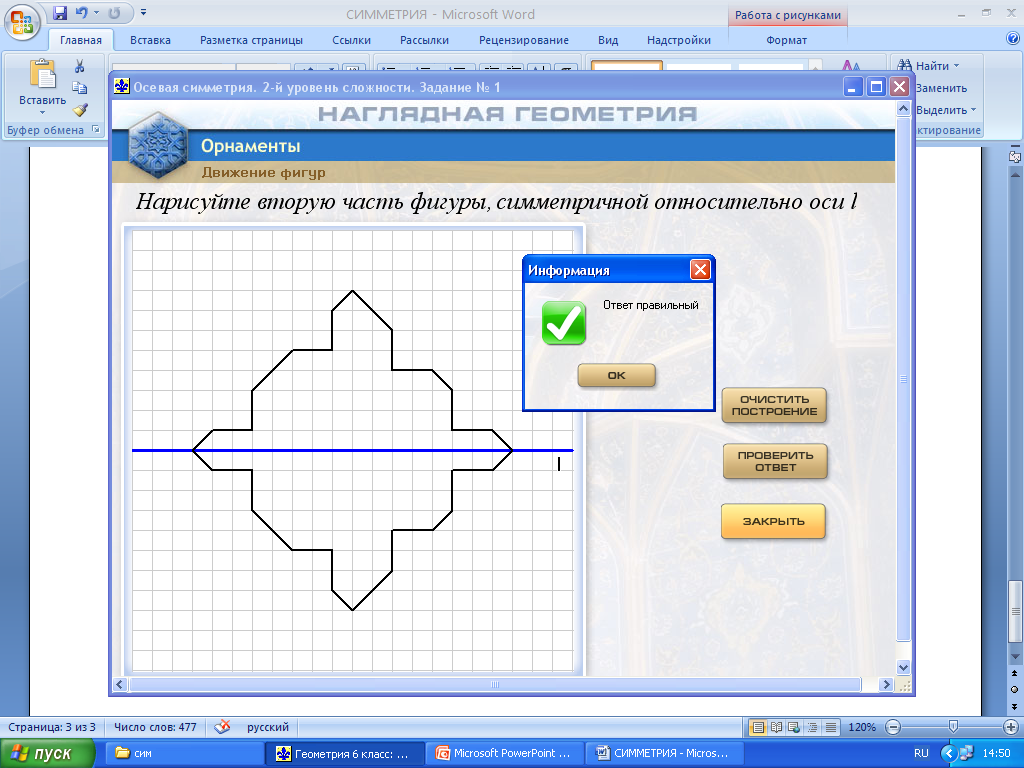
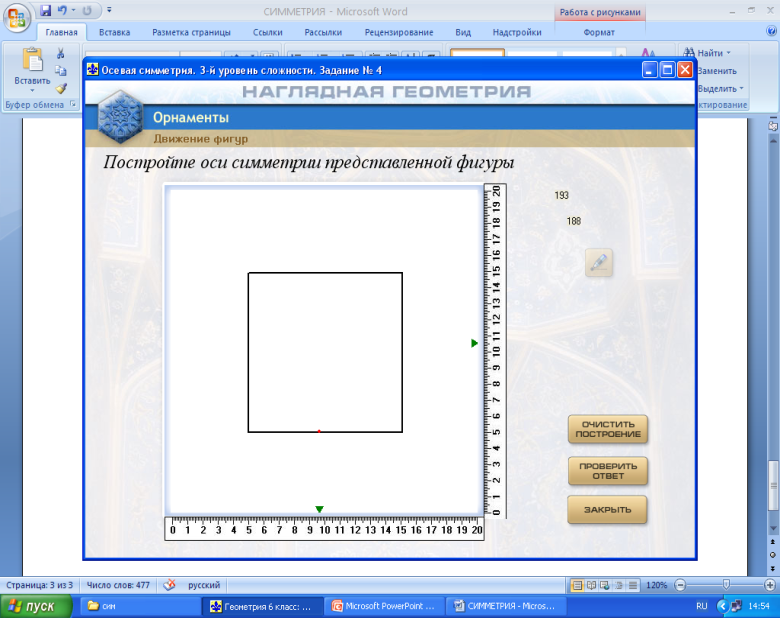
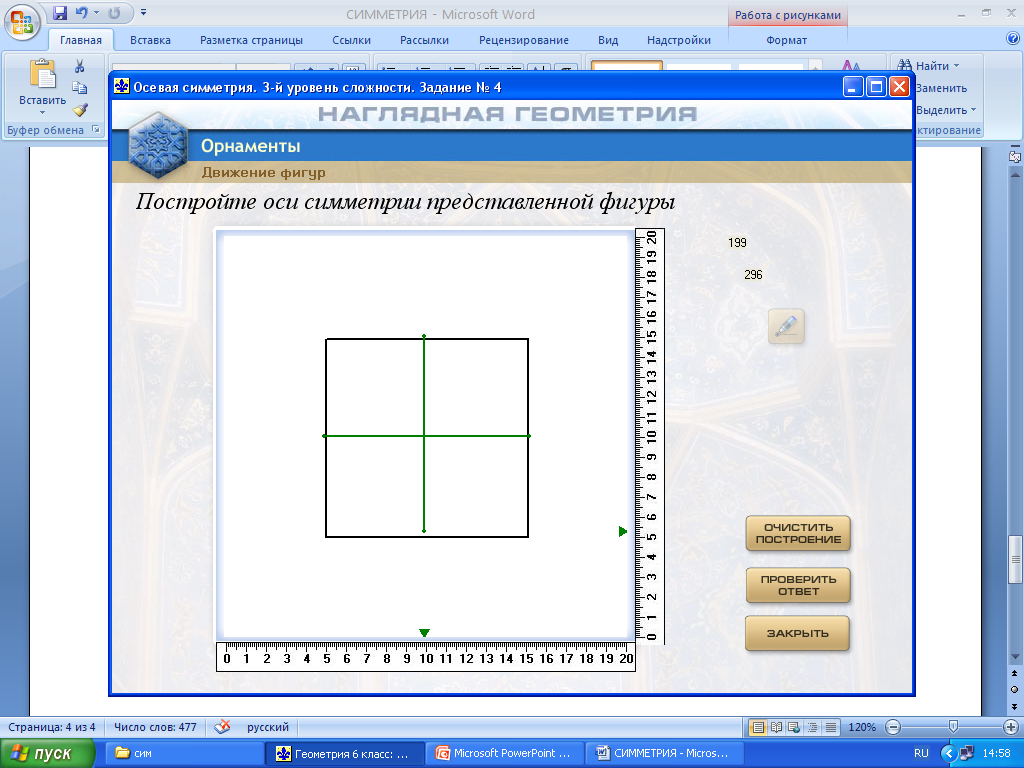
Работа с программным комплексом «Наглядная геометрия». Программа «Орнаменты». Учащиеся занимают места за компьютерами. Возможна парная работа, а при наличии достаточного числа техники (дополнительно использовать ноутбуки, планшеты) работа индивидуальная. Последняя форма работы на уроке предпочтительнее. Учитель дает рекомендации по работе с ресурсом и напоминает про правила работы за компьютером.
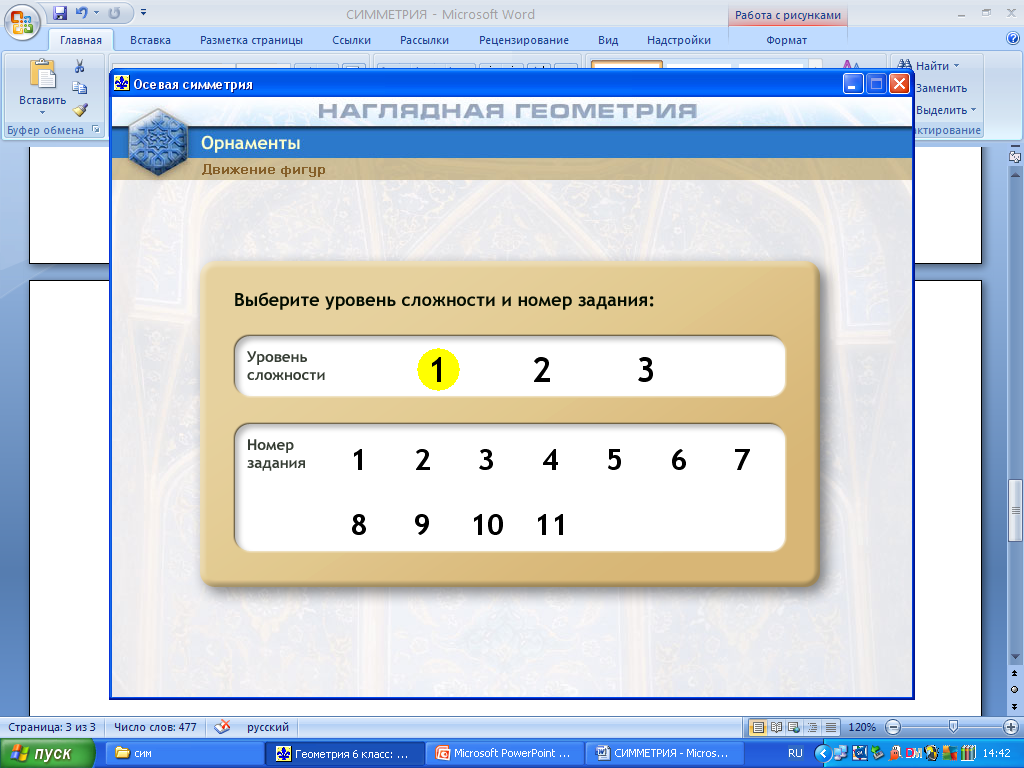
Действия: Движения фигур – Осевая симметрия – Выбор уровня сложности задания – Номер задания.
Предлагается учащимся выбрать сначала уровень 1 (задания 1 и 2), затем уровень 2 (задание 1), уровень 3 (задание 4). Учащиеся, которые успешно справились с предложенными упражнениями раньше остальных, выполняют остальные задания уровня 3.
На рисунках показаны этапы работы с ЦОРом.
6. Домашнее задание.
Параграф 29 стр.160, задание 1 стр.164, задание к рисунку 250, стр.164.
7. Рефлексия. Подведение итогов.
— С каким математическим понятием мы познакомились на уроке?
— Какой вид симметрии изучили?
— Как построить точку симметричную данной относительно прямой?
— Приведите пример геометрических фигур, имеющих ось или оси симметрии.
— Буквы русского языка тоже можно рассмотреть с точки зрения симметрии. Из предложенных букв (приложение 3) выберите симметричные и составьте с помощью этих букв слово. (А,Б,В,Г,Е,И,Н,Р,С — ВЕСНА). (Если времени недостаточно, то можно заменить данное задание вопросом: Какие буквы русского алфавита имеют оси симметрии?
— Где в природе и деятельности человека можно встретиться с симметрией? Приведите примеры.
Учитель: Но симметрия встречается во многих других сферах деятельности человека. И мы с вами на следующих уроках будем говорить об этом. А закончить наш урок мне хотелось бы прослушиванием музыкального произведения «Вальс» Г.Свиридова к повести А.С. Пушкина «Метель». Как вы думаете, какое отношение может иметь это произведение к нашему сегодняшнему уроку? (Ответы учащихся). Действительно, различные виды симметрии могут встречаться и в музыке, и это довольно частое явление. В «Вальсе» Свиридова используется трансляционный вид симметрии, который является самым распространенным видом симметрии в музыке. В этом случае музыкальная фраза (мелодия или более крупные отрывки музыкального произведения) повторяется, оставаясь неизменной. (Прослушивание небольшого фрагмента музыкального произведения, после которого учитель благодарит учащихся за урок).
ЛИТЕРАТУРА И ССЫЛКИ.
1. Видео ролик «Отзвуки вальса» (http://narod.ru/disk/64744485001.3b1812c8502c25f27f16039fa092f298 /Г.Свиридов%20-%20Отзвуки%20вальса.mp4.html ),
2. Программный комплекс «Наглядная геометрия» (Единая коллекция цифровых образовательных ресурсов. Программа «Орнаменты» http://school-collection.edu.ru/catalog/rubr/f9aff3d4-713b-4a6e-a064-24a0d8733e6d/104804/?interface=catalog&class=47&subject=18 ),
3. Ресурс «Осевая симметрия» из Единой коллекции цифровых образовательных ресурсов.
http://files.school collection.edu.ru/dlrstore/7ae32a0c-0a01-01b2-0162-f030dc1675ee/%5bG89D_8-01-04-10%5d_%5bML_104%5d.swf