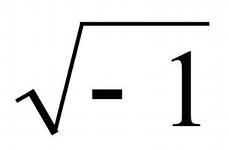Математическая викторина «Из истории цифр и чисел»
( 10-11 класс)
Составила учитель математики
МБОУ «Джалильская гимназия»
Сармановского района Республики Татарстан
Мухамадиева Гульнара Дамировна
Вопрос №1
Искусство счета развивалось с развитием человечества. В древности для счета хватало всего четырех слов: один, два, три и много. Способов счета придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Это было неудобно. Пришлось придумать систему счисления.
Как называется эта система счисления ?
-
натуральная;
-
десятичная;
-
цифровая;
-
бесконечная.
Ответ: Палку с зарубками с собой не возьмешь, камни таскать не очень приятно, пастуху надо знать – не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук – отличный счетный материал. А если предметов больше десяти? Тут и появилась десятичная система счисления.
Вопрос №2
Тысяча тысяч – это миллион. Тысяча миллионов — это биллион или миллиард. Тысяча миллиардов, т.е. 1 000 000 000 000 – триллион, дальше 1000 000 000 000 000 – квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион, дециллион. Все числа пересчитать невозможно. Физики подсчитали, что количество атомов – мельчайших частиц вещества – во всей Вселенной не превосходит некоторого числа, выражаемого единицей со ста нулями.
Какое название получило это число?
-
бесконечность;
-
астрономическое число;
-
гугол;
-
тьма.
Ответ: В 1938 году американский математик Эдвард Казнер гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта, предложил назвать это число «гугол» (googol). В 1940 году Эдвард Казнер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение» («New Names in Mathematics»), где и рассказал любителям математики о числе гугол.
Вопрос №3
Среди астрономических чисел все таки есть самое большое число, которое имеет свое название – это единица с 600 нулями.
Как называется это число?
-
бесконечное;
-
центиллион;
-
космическое;
-
у этого числа нет названия.
Ответ: Наибольшим числом, которым оперируют математики, является центиллион. Это 1 с 600 нулями. Любое число свыше центиллиона рассматривается как абстрактное, лежащее в бесконечности. Хотя предпринимались попытки определить такие абстракции.
Вопрос №4
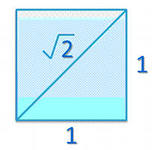
Когда торговцам и ремесленникам чисел было уже достаточно, математики Древней Греции, ученики Пифагора , обнаружили, что есть числа ,которые не выражаются никакой дробью. Первым таким числом стала длина диагонали квадрата.
Как называют такое число?
-
неизвлекаемое;
-
арифметический корень;
-
иррациональное;
-
периодическое.
Ответ: Это открытие так поразило пифагорийцев, что они долгое время это держали в тайне. Новые числа стали называть иррациональными – недоступными пониманию, а целые числа и дроби – рациональными.
Вопрос №5
В Европе признание этих наступило на тысячу лет позже, чем в Китае. Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который трактовал эти числа как долг. Бомбелли и Жирар в своих трудах считали такие числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Индийские математики представляли себе числа — “имущества” и числа — “долги”
Как называют такие числа?
-
мнимые;
-
абсурдные;
-
отрицательные;
-
невозможные.
Ответ: В Европе отрицательными числами начали пользоваться с XII–XIII вв., но до XVI в., как и в древности, они понимались как долги, большинство ученых считали их “ложными”, в отличие от положительных чисел – “истинных”.
Вопрос №6
Казалось бы, уже все, больше никаких чисел не придумать, но в ряде случаев возникает потребность найти число, квадрат которого равен минус единице. Среди известных чисел такого не оказалось, поэтому его обозначали буквой i.
Как называется это число?
-
невозможное;
-
абстактное;
-
мнимое;
-
ложное.
Ответ: Такое число назвали мнимой единицей. Числа , полученные умножением ранее известных чисел на мнимую единицу, стали называть мнимыми.
Вопрос №7
Цифры, которые мы используем при счете предметов, разработаны индусами. А в Европу из Индии кто передал записи этих чисел?
-
египтяне;
-
индусы;
-
арабы;
-
римляне.
Ответ: Цифры современной десятичной системы носят название арабских, поскольку европейцы заимствовали их у арабов. Однако, их родина – южная Индия. Они встречаются во множестве документов, относящихся к VI-IX вв.
Вопрос №8
В русской математической литературе это число не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.
Какое это число:
-
отрицательное;
-
дробное;
-
ноль;
-
мнимое?
Ответ: Одного открытия древние греки не сделали. Они не придумали ноля. Кто первым догадался обозначить цифрой «ничто»? Таких гениев было несколько. Кто-то придумал знак нуля в Древней Греции, кто-то из индейцев май – в Америке, кто-то в Китае. И кто-то из мудрецов Индостана обозначил пустое место тем самым кружком, которым мир пользуется до сих пор.
Вопрос №9
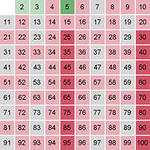
Древнегреческий математик придумал способ нахождения простых чисел. Если записать все числа от 1 до 100, то начинаем вычеркивать все числа, которые делятся на 2, потом на 3, потом на 5 и так далее.
Как называется этот метод?
-
метод деления;
-
метод перебора;
-
решето Эратосфена;
-
метод зачеркивания.
Ответ: Этот метод придумал математик Эратосфен, в честь которого называется этот метод решетом Эратосфена.
Вопрос №10
Сумма действительных и мнимых чисел дают новый вид числа. Появилось расширение множества вещественных чисел, которое обычно обозначают буквой 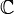
Это множество называется :
-
множество вещественных чисел;
-
множество мнимых чисел;
-
множество нереальных чисел;
-
множество комплексных чисел.
Ответ: Комплексным числом 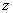 называется число вида
называется число вида 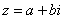 , где
, где 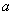 и
и 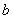 – действительные числа,
– действительные числа, 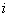 – так называемая мнимая единица. Число
– так называемая мнимая единица. Число 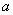 называется действительной частью комплексного числа
называется действительной частью комплексного числа 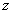 , число
, число 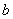 называется мнимой частью комплексного числа
называется мнимой частью комплексного числа 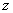 . А само множество называется множеством комплексных чисел.
. А само множество называется множеством комплексных чисел.
Вопрос №11
Название какого числа выбивается из однотипных названий чисел, которые являются числами, кратными десяти:
-
девяносто;
-
девятьсот;
-
сорок;
-
сто?
Ответ: В русском языке названия числительных до 100, делящихся на 10, образуются сложением названия цифры и «десять»: двадцать, тридцать, пятьдесят и т. д. Исключением из этого ряда является число «сорок». Объясняется это тем, что в древности условной единицей торговли меховыми шкурками была связка из 40 их штук. Ткань, в которую заворачивались эти шкурки, и называлась «сорок» (от этого же корня происходит слово «сорочка»). Таким образом название «сорок» вытеснило более древнее «четыре десте».
Вопрос №12
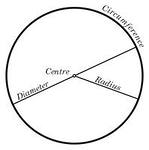
Отношение длины окружности к диаметру постоянно, не зависит от радиуса круга. Эта постоянная величина имеет два неофициальных праздника. Как называется это число ?
-
рациональное;
-
целое;
-
е;
-
пи.
Ответ: У числа Пи есть два неофициальных праздника. Первый – 14 марта, потому что этот день в Америке так называется 3.14. Второй – 22 июля, которое европейском формате записывается 22/7, а значение дроби является достаточно популярным приближенным значением числа Пи.
Вопрос №13
В школе Пифагора занимались изучением семеричности. Ее суть состоит в том, что «семь» как магическое число определяет многие взаимосвязи в мире. Сам Пифагор написал трактат:
-
«Магическая семерка»;
-
«Волшебная семерка»;
-
«Все о 7»;
-
«Семеричность».
Ответ: «Магическая семерка». Этот трактат в оригинале, к сожалению, не сохранился, но можно утверждать, что первые четыре раздела геометрии Евклида представляют собой пересказ этого трактата. Итак, все в мире подсинено семеричности:
7 чудес Света; 7 мудрецов; 7 звезд в ковше Большой медведицы и столько же в Малой медведице; 7 нот; 7 идеальных тел в стереометрии (это тела, грани которых образованы правильными фигурами: тетраэдр, куб, пентаэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр); 7 лет составляет цикл жизни человека: 7 лет длится детство, 7 лет – отрочество, 7 лет – юность, 7 лет – молодость и т.д.; согласно современным исследованиям социопсихологов, человек одновременно может удержать в поле своего внимания 7 предметов.
Вопрос №14
Множество закономерностей, возникающих при действиях с числами, были обнаружены древнегреческими учеными при изучений чертежей. И долгие века лучшим подтверждением справедливости таких соотношений считался способ геометрический, с прямоугольниками, квадратами, пирамидами и кубами. Есть общее название чисел, геометрическое представление которых связано с той или иной геометрической фигурой. Это числа :
-
фигурные;
-
геометрические;
-
круглые;
-
многоугольные.
Ответ:. В V — IV веках до нашей эры ученые, комбинируя натуральные числа, составляли из них затейливые ряды, придавая элементам этих рядов то или иное геометрическое истолкование. С их помощью можно выложить правильные геометрические фигуры: треугольники, квадраты, пирамиды и т.д. Увлеклись, причем независимо друг от друга, нахождением таких фигурных чисел Б. Паскаль и П. Ферма.
Вопрос №15
Существуют натуральные числа , равные сумме всех своих собственных делителей (т. е. всех положительных делителей, отличных от самого́ числа). По мере того как натуральные числа возрастают, эти числа встречаются всё реже. Они имеют свое название:
-
идеальные числа;
-
совершенные числа;
-
исключительные числа;
-
красивые числа?
Ответ: Совершенные числа. Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные совершенные числа, можно получить из формулы: 2p–1 (2p– 1) при условии, что р и 2p есть числа простые. Таким путём было найдено около 20 чётных совершенных чисел. До сих пор (1976) неизвестно ни одного нечётного совершенного числа и вопрос о существовании их остаётся открытым. Исследования о совершенных числах были начаты пифагорейцами, приписывавшими особый мистический смысл числам и их сочетаниям.
Вопрос №16
Пифагор говорил: «Мой друг тот, кто является моим вторым я, как числа 220 и 284».Эти числа замечательны тем , что сумма делителей каждого из них равна второму числу.1+2+4+5+10+11+20+22+40+44+55+110=284, 1+2+4+71+142=220.
Эти числа называются:
-
дружественными;
-
парными;
-
взаимосвязанными;
-
взаимными?
Ответ: Дружественные числа, пара натуральных чисел, каждое из которых равно сумме всех собственных (или правильных) делителей другого, т. е. делителей, отличных от самого числа. Приписывая мистический смысл свойствам чисел, пифагорейцы придавали дружественным числам большое значение Около 60 пар дружественных чисел было найдено Л. Эйлером . Использование ЭВМ позволило отыскать ещё несколько сотен пар таких чисел. Эти числа представляют в первую очередь исторический интерес.
Вопрос №17
Существует такой ряд чисел, где элементы числовой возвратной последовательности 1, 1, 2, 3, 5, 8,… в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо Пизанского . Этот ряд чисел назвали:
-
арифметический ряд чисел;
-
ряд Фибоначчи;
-
числа Пизанского;
-
геометрическая прогрессия.
Ответ: Числовой ряд, носящий сегодня его имя, вырос из проблемы с кроликами, которую Фибоначчи изложил в своей книге «Liber abacci», написанной в 1202 году: Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? Можете убедиться, что число пар в каждый из двенадцати последующих месяцев будет соответственно
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Вопрос №18
Существуют такие комплексные или вещественные числа, которые не являются корнем многочлена с целыми коэффициентами. И эти числа называются:
-
переходными;
-
превосходящими;
-
трансценде́нтными;
-
иррациональными.
Ответ: еще древние греки знали замечательное число пи , которое, как выяснилось впоследствии, трансцендентно, но они знали его только как отношение длины окружности к ее диаметру. Вопрос об истинной природе этого числа вообще мало кого интересовал до тех пор, пока люди вдоволь и безуспешно не нарешались древнегреческой задачей о квадратуре круга, а само число пи каким-то загадочным образом повылезало в разных разделах математики и естествознания.
Лишь только в 1844 году Лиувилль построил исторически первый пример трансцендентного числа, а математический мир удивился самому факту существования таких чисел. Лишь только в 19 веке гениальный Георг Кантор понял, используя понятие мощности множества, что на числовой прямой трансцендентных чисел подавляющее большинство. Лишь только в пятом параграфе этой небольшой книжки мы, наконец-то, обратим на трансцендентные числа свое внимание.
Вопрос №19
В теории чисел существует число , которое является натуральным числом множества, генерируемого «решетом», аналогичным решету Эратосфена , которое генерирует простые числа .
Начнем со списка целых чисел , начиная с 1:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
Каждое второе число (все четные числа) исключается, остается только нечетные числа :
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25,
Второй член в этой последовательности 3. Каждое третье число, которое остается в списке, исключается:
1, 3, 7, 9, 13, 15, 19, 21, 25,
Теперь третье оставшееся число это 7, поэтому каждый седьмой номер, который остался, исключается:
1, 3, 7, 9, 13, 15, 21, 25,
Такие числа называются:
-
простыми;
-
счастливыми;
-
удивительными;
-
интересными.
Ответ: Процедура постоянно повторяется, оставшиеся числа и будут счастливыми числами: 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, …
Вопрос №20
Числа , которые можно записать нетривиальным путём, используя все цифры , входящие в число, операции сложения, вычитания, умножения, деления, возведения в степень и сочленения цифр (сочленение цифр m и n, есть число mn, то есть число m × 10 + n), входящих в число, называются:
-
самовыражающие;
-
числами Фридмана;
-
числами Гаусса;
-
числами Виета.
Ответ:Так числа 2,5 и 126 будут являться числами Фридмана, потому что 2,5 = 5 : 2, а 126 = 6 × 21. Число 25 — единственное двузначное число Фридмана, трёхзначных чисел больше — их тринадцать: 121 , 125 , 126 , 127 , 128 , 153 , 216 , 289 , 343 , 347 , 625 , 688 , 736.