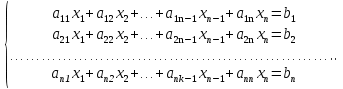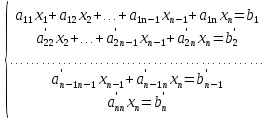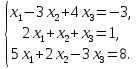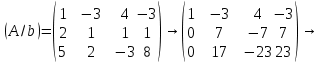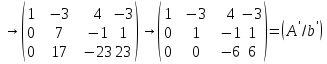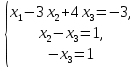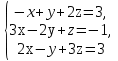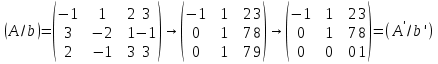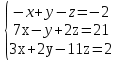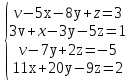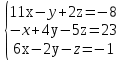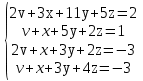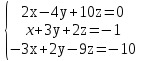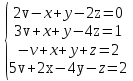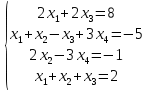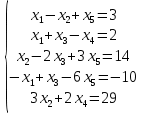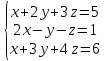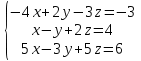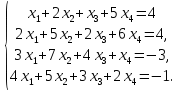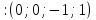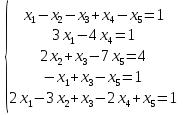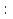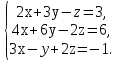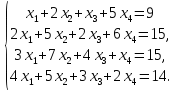ГБОУ средней общеобразовательной школы №618 г. Москвы
Конспект урока
по теме
«Системы линейных уравнений.
Метод Гаусса»
Предмет: алгебра
Контингент: 9 – 11 класс
Тип урока: урок — лекция
Автор:
Макарова Татьяна Павловна,
учитель математики
ГБОУ средней общеобразовательной школы №618
г. Москвы
Конспект урока по теме «Системы линейных уравнений. Метод Гаусса»
Автор:
Макарова Татьяна Павловна,
учитель математики
ГБОУ средней общеобразовательной школы №618 г. Москвы
Цели урока:
-
Формирование и закрепление у учащихся навыков решения систем линейных уравнений методом Гаусса.
Задачи урока:
-
Сформировать навыки и умения решения систем линейных уравнений, используя метод Гаусса.
-
Прививать интерес к предмету через привлечение различных источников информации; расширять кругозор учащихся; способствовать формированию исследовательских и коммуникативных компетенций, навыков само- и взаимопроверки.
-
Развивать логическое мышление, способность к абстрагированию, анализу.
-
Воспитывать самостоятельность и активность учащихся.
Тип урока: урок – лекция
Методы и педагогические приёмы:
• словесный метод;
• наглядный метод;
• методы самостоятельной учебной работы и работы под руководством учителя;
• методы контроля (устный, письменный);
• методы самоконтроля и взаимоконтроля;
• дифференцированная работа.
Формы организации совзаимодействия на уроке: учебная, групповая работа, индивидуальная работа
Оборудование: раздаточный материал
Контингент: 9-11 классы
Ход урока
I. Организационный момент (приветствие учащихся).
II. Актуализация.
Продолжаем рассматривать системы линейных уравнений.
Сначала немного систематизируем знания о системах линейных уравнений.
Фронтальный опрос:
-
Сколько решений может иметь система линейных уравнений?
Предполагаемый ответ учащихся:
Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
-
Какие методы решения систем линейных уравнений вы знаете?
Предполагаемый ответ учащихся:
Метод подстановки, сложения, графический метод.
III. Основная часть.
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений.
Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто!
Метод Гаусса — метод последовательного исключения неизвестных.
Рассмотрим систему, состоящую из n уравнений первой степени с n неизвестными, или систему линейных уравнений.
(1)
Первый индекс коэффициентов при неизвестных обозначает номер уравнения, а второй — номер переменной. Такая система может быть несовместной, если она не имеет решения, и совместной, если имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определенной, а более одного — неопределенной.
При помощи элементарных преобразований сначала исключаем из всех уравнений, кроме первого, переменное x1. Далее исключаем из всех уравнений, кроме первого и второго, переменную x2 и так далее. В конечном итоге мы приходим к системе следующего вида:
(2)
Если в полученной системе (2) в последнем уравнении свободный член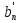 
не равен нулю, а коэффициент 
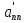в левой части равен нулю, то исходная система (1) несовместна, т.е. не имеет решений. Если в системе (2) все коэффициенты в левой и правой части последнего уравнения равны нулю, тогда система (1) будет совместной неопределенной. В остальных случаях система будет обладать единственным решением.
Напомним, что к элементарным преобразованиям системы относятся следующие:
1). Перемена местами двух уравнений в системе;
2). Умножение какого — либо уравнения системы на действительное число, не равное нулю.
3). Прибавление к одному уравнению другого уравнения, умноженного на произвольное число, не равное нулю.
Системы линейных уравнений (1) и (2) являются эквивалентными, т.к. множество их решений совпадают.
На практике более удобным оказывается применение метода Гаусса не, собственно, к самой системе линейных уравнений, а к ее расширенной матрице. Когда расширенная матрица будет приведена к треугольному виду, на этом цепь элементарных преобразований над матрицей завершается.
Пример 1. Найти решения системы уравнений:
Решение. Выпишем расширенную матрицу данной системы. Первый столбец будет стоять из коэффициентов, находящихся при переменной х1, второй столбец — соответственно из коэффициентов при х2, третий столбец — из коэффициентов при х3, четвертый столбец расширенной матрицы — из свободных членов.
Расширенная матрица коэффициентов исходной системы (A/b) сводится к треугольной матрице (A’/b’) последовательными элементарными преобразованиями:
1). Первая строка матрицы (А/b) умножается на (-2) и на (-5) и прибавляется соответственно ко второй и третьей строке.
2). Вторая строка умножается на 1/7.
3). К третьей строке прибавляем вторую, умноженную на (-17).
Треугольная система, соответствующая матрице (A’/b’) имеет вид:
Откуда единственное решение системы находится следующим образом: x3= –1;из второго уравнения x2=1+x3=0;из первого уравнения x1=–3+3x2 – 4x3=1.
Таким образом, тройка чисел (1;0;-1) является решением исходной системы линейных уравнений, что можно легко проверить подстановкой.
Пример 2. Решите систему уравнений:
Решение.
Последней строке матрицы (A’/b’) соответствует уравнение эквивалентной системы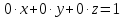 
, которое не имеет решений.
Ответ: решений нет.
III. Закрепление пройденного материала. Работа в группах.
Задание. Решить систему уравнений методом Гаусса.
| Задание. Решить систему уравнений методом Гаусса. | Ответ | |
| 1 | | 1.(3,2,1) 2. решений нет |
| 2 | |
|
| 3 | | 1.(11;-2;-3) 2.(1;1;1;1) |
| 4 |
| 1.(2;-2;2;-1) 2. (11;7;-5;4;-1) |
Закрепление пройденного материала. Самостоятельная работа.
| Вариант 2 | |
| 1. Решить систему уравнений методом Гаусса. | |
| а) Ответ: (1 ; -1; 2) | а) Ответ: нет решений |
| б) Ответ | б) Ответ |
IV. Подведение итогов урока. Рефлексия.
Выбери вариант соответствующий твоим ощущениям после сегодняшнего занятия.
1. Я все знаю, понял и могу объяснить другим!
2. Я все знаю, понял, но не уверен, что смогу объяснить другому.
3. Я сам знаю, понял, но объяснить другому не смогу.
4. У меня остались некоторые вопросы.
V. Домашняя работа.
Решить системы уравнений методом Гаусса:
Ответ: бесконечное множество решений.
.
VI. Список использованной литературы
1 . http://www.mathprofi.ru/metod_gaussa_dlya_chainikov.html