| Организационная информация | |
| Тема урока | Квадратные уравнения: методы решения. |
| Предмет | Алгебра. |
| Класс | 8. |
| Автор урока | Шамшина Наталья Васильевна |
| Республика/край, город/поселение | Воронежская область, п.г.т.Анна |
| Методическая информация | |
| Тип урока | Урок формирования знаний. |
| Цели урока | Познакомить учащихся с общими и специальными методами решения квадратных уравнений. |
| Задачи урока | Образовательные: повторить — определения квадратного уравнения, приведённого квадратного уравнения, неполного квадратного уравнения, алгоритмы их решения — формулы дискриминанта и корней квадратного уравнения, теорему Виета (прямую и обратную). знать — виды и суть общих и специальных методов решения квадратных уравнений, фамилии учёных, связанных с открытиями в области квадратных уравнений, уметь — выбирать рациональный способ решения квадрат ных уравнений; делать мультимедийные презентации; осуществлять поиск и отбор учебного материала. Воспитательные: воспитывать ответственность, инициативность, настойчи вость, дисциплинированность, взаимопомощь. Развивающие: развивать логическое мышление, внимание, умение аргу ментировать, делать выводы, умение работать в группе; расширять кругозор, формировать грамотность математи ческой речи, интерес к математике. |
| Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока | • Повторят определения квадратного уравнения, приведён • Приобретут знания о видах и сути общих и специальных • Закрепят коммуникативные умения, умения выбирать • Получат развитие: логическое мышление, внимание, уме |
| Необходимое оборудование и материалы | Мультимедийный проектор, компьютер, экран, листы самоконтроля для каждого ученика (образец см. презентацию). |
| Подробный конспект урока | |
| Мотивация учащихся | В начале урока учитель знакомит учащихся с целями и задачами урока, правилами работы на уроке |
| Ход и содержание урока | |
Предварительная подготовка.
За неделю до урока ученики делятся учителем на группы (разноуровневые). Каждая группа получает задание (с комментариями и рекомендациями учителя) — рассмотреть один из специальных или общих методов решения квадратных уравнений, а также сделать презентацию по этому материалу. Перед представлением на уроке проделанной работы группы отчитываются перед учителем (контролируется участие каждого ребёнка), получают у него консультации, а также решают вопрос о том, кто будет представлять группу на уроке.
Ход урока.
I. Организационный момент, (формирование мотивации работы учащихся). Учитель:
-
приветствует учащихся,
-
проверяет готовность к уроку,
-
объявляет тему «Специальные и общие способы решения квадратных уравнений»,
-
объявляет цели урока,
-
озвучивает план работы (слайд — 1-3):
• объясняет правила заполнения листа самоконтроля.
Приложения к уроку — «Лист самоконтроля», буклет «Способы решения квадратных уравнений».
П. Теоретическая разминка (актуализация знаний). Форма работы: фронтальная.
Ученики отвечают на вопросы теоретической разминки, которые размещены на слайде 4:
-
виды квадратных уравнений;
-
определение неполных квадратных уравнений;
-
виды неполных квадратных уравнений;
-
способы решения неполных квадратных уравнений;
-
приведенное квадратное уравнение.
Проверка ответов осуществляется с помощью слайдов № 12-15 и устное закрепление (слайды №35-37 по ссылкам). После этого ученики ставят отметку в листе самоконтроля.
III. Энциклопедия квадратных уравнений. Рассматриваются общие и специальные методы решения на слайдах №5 и №6. Общие методы:
• Метод выделения квадрата двучлена (слайд 21 и 28).
Суть метода: привести уравнение общего вида к неполному квадратному уравнению. Используются формулы сокращенного умножения, а именно, квадратов суммы и разности:(а + b)2 = a2 + 2ab + b2, (a— b)2 = a2— 2ab + Ь2. Иногда имеет смысл применить формулу разности квадратов.
Пример. Решим уравнение х +6х -9 = 0.
Зх2+6х-9 = 0,
х2+2х-3 = 0,
(х+1)2— 4 = 0,
(x+l)2 = 4,
x+ 1=2 и х+ 1 = — 2,
x = 1, x = — 3.
Ответ: — 3; 1.
Примечание: метод можно применять для любых квадратных уравнений, но он не всегда
удобен в использовании.
• С помощью формул дискриминанта (D и D1) и корней квадратного уравнения (слайд
17-19).
• Метод разложения на множители (слайд 24 и 32).
Суть метода: привести квадратное уравнение общего вида к виду А(х)*В(х) = 0, где
А(х) и В(х) — многочлены относительно х.
Способы: вынесение общего множителя за скобки; использование формул сокращенного умножения; способ группировки.
Пример. Решите уравнение Зх2 + 6х — 9 = 0.
Зх2+6х-9 = 0,
Зх2+9х-Зх-9 = 0,
(Зх2 — Зх) + (9х- 9) = 0,
Зх(х-1) + 9(х-1) = 0,
(х-1)(Зх+9) = 0,
x — 1 = 0 или Зх + 9 = 0,
х=1, Зх = -9,
х = -3.
Ответ: -3, 1.
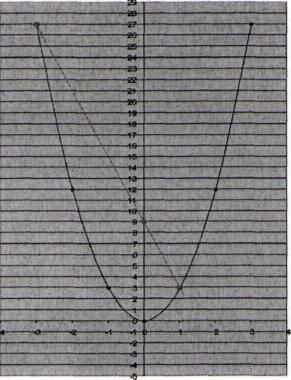
• Графический метод (слайд 26 — 27).
Для решения уравнения f(x) = g(x) необходимо построить графики функций у = f(x), у = g(x) в одной прямоугольной системе координат и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения.
Применение этого метода при решении квадратного уравнения Зх2 +6х -9 = 0. Построим график функции у=3х2.
| X | 3 | 2 | 1 | 0 | -1 | -2 | -3 | ||||
|
| Y | 27 | 12 | 3 | 0 | 3 | 12 | -27 | |||
|
|
|
|
| ||||||||
| X | 0 | 1 |
|
| |||||||
| Y | 9 | 3 |
|
| |||||||
Графиком является парабола, «ветви» которой направлены вверх, (0;0) — вершина параболы, график симметричен относительно оси ординат.
Построим график функции у = -6х + 9. Линейная функция. Графиком является прямая.
Точки пересечения: А(1;3) и В(-3;27).
Ответ: -3;1.
Графический метод удобен для нахождения количества корней.
-
применение теоремы, обратной теореме Виета.
Решить уравнение Зх +6х-9 = 0на доске с помощью теоремы, обратной теореме Виета Зх2+6х-9 = 0,
х2 + 2х-3 = 0,
x1 х2 = — 3,
х, =-3,
x2 = 1.
Ответ: x1 = — 3, х2 = 1.
• Метод «переброски» старшего коэффициента (слайд 22, 29).
Суть метода: известно, что корни квадратных уравнений ax2 + bx + c = 0 и у + by + ас = 0 связаны соотношениями: x1 = y1/a, x2 = y2/a
Поэтому иногда удобно решать не данное уравнение ах2 + bх + с = 0, а приведённое у2 + by + ас = 0, которое получается из данного «переброской» коэффициента а, а затем разделить найденные корни на а для нахождения корней исходного уравнения.
Пример. Решите уравнение Зх2+ 6х -9 = 0.
Заменим данное уравнение приведённым квадратным уравнением с «переброской» коэффициента а: у2 +6у — 27 = 0. D>0, по теореме, обратной теореме Виета, получаем корни: 3; — 9, далее возвращаемся к корням исходного уравнения: 1; — 3.
Ответ: — 3; 1.
Примечание: метод применяется для квадратных уравнений с «удобными» коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.
• По свойству коэффициентов. Теоремы (слайды 23, 30).
Теорема 1. Если в квадратном уравнении а + b + с = 0, то один из корней равен 1, а второй по
теореме Виета равен c/a.
а
Пример. Решите уравнение Зх + 6х — 9 = 0.
Зх2+6х-9 = 0,
а= 3,b = 6, с = -9,
а + b+ с = 3 + 6 — 9 =0,
x1 = 1,
x2 = c/a = — 3
Ответ: — 3; 1.
IV. Физкультминутка (слайд 41 — 44).
V. Исторический справка (начало — слайд 7-9, 46). История алгебры уходит своими корнями в древние времена.
Задачи, связанные с уравнениями решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.
В древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто представлялись в стихотворной форме. Задача знаменитого индийского математика XII века Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок.
Ты скажи мне, в этой стае?
Решение:
VI. Копилка ценных мыслей
Учащимся предлагается буклет, в котором представлено решение уравнения Зх2 + 6х — 9 = О семью различными способами.
| Проверка и оценивание ЗУНКов | VII. Самостоятельная работа со взаимопроверкой (слайд 38 — 40) 1 вариант 2 вариант 1) 2х2+Зх-5=0, 1) Зх2+5х-2=0, 2)Зх2-27=0, 2)18-2х2=0, 3) х2+2х=0, 3) 3х-х2=0, 4) 21х2-5х+1=0, 4) х2+25=0, 5) х2+36=0, 5) 5х2-26х+5=0, 6) 4х2-28х+49=0 6) 2х2-5х+3=0 | |
|
| Рефлексия деятельности на уроке | Учащимися заполняется лист самоконтроля и сдаётся учителю. |
|
|
|
|
| VI. Домашнее задание (слайд 12). | |
|
| 1. Решите уравнение Зх2+5х + 2 = 0 всеми возможными способами. |
|
| 2. Дополнительно. |
|
| Решите уравнение (х2-х) — 14(х2-х) + 24 = 0 методом введения новой |
|
| переменной. |
| Использованные | |
| источники и литера- | |
| тура |
|
| Обоснование, поче- | Использование мультимедийной презентации позволяет доступно с высо- |
| му данную тему оп- | кой степенью наглядности представить большой объём учебного мате- |
| тимально изучать с | риала. Обеспечивается высокий уровень контроля за информацией — ин- |
| использованием ме- | формация появляется тогда, когда это необходимо, и столько сколько не- |
| диа-, мультимедиа, | обходимо раз (возможен возврат к уже просмотренному материалу). Воз- |
| каким образом осу- | можность задействовать все виды памяти школьников, что повышает ка- |
| ществить | чество усвоения учебного материала. |
| Советы по логиче- | Следующий урок можно провести в нестандартной форме (например, ко- |
| скому переходу от | мандного соревнования) с целью закрепления изученного материала. |
| данного урока к по- |
|
| следующему |
|
|
|
|