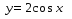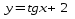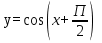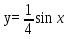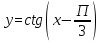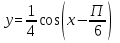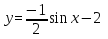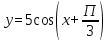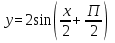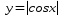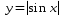Преобразование графиков тригонометрических функций, 10 класс

Конспект урока по алгебре в 10 классе

Васильева Екатерина Сергеевна,

учитель математики

ОГБОУ «Смоленская специальная (коррекционная)

общеобразовательная школа I и II видов»

Смоленск

Тема урока: «Преобразование графиков тригонометрических функций».

Название модуля: преобразование графиков тригонометрических функций.

Интегрирующая дидактическая цель: отработать навыки построения графиков тригонометрических функций.

Целевой план действий для учащихся:

• повторить основные свойства тригонометрических функций;

• отработать навык преобразования графиков тригонометрических функций;

• способствовать развитию логического мышления;

• воспитывать интерес к изучению предмета.

Банк информации.

Входной контроль.

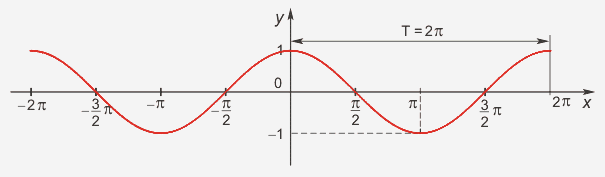
Назовите свойства функций y = sin x (рис. 1).

Рис. 1

Свойства:

1. D(y)=R

2. E(y)=[-1;1], функция ограничена

3. sin(-x)=-sinx, функция нечётная

4. Наименьший положительный период: 2π
   sin (x+2πn)= sin x, n Є Z, x Є R.

5. sin x=0 при x=πk, kЄ Z

6. sin x>0, x Є (2πk;2π+2πk), k Є Z

7. sin x<0, x Є(π+2πk; 2π+2πk), k Є Z

8. Наибольшее значение, равное 1, y=sin x принимает в точках x=π/2+ 2πk, k Є Z.

9. Наименьшее значение, равное -1, y=sin x принимает в точках x=3π/2+ 2πk, k Є Z.

Рассмотрим график фукции y= cos x (рис. 2).

Рис. 2

Свойства:

1. D (y)=R

2. E (y)=[-1;1], функция ограничена

3. cos(-x)= cos x, функция чётная

4. Наименьший положительный период: 2π
   cos (x+2πn)=cos x, n Є Z, x Є R

5. cos x=0 при x=π/2+πk, kЄZ

6. cos x>0, x Є (-π/2+2πk; π/2+2πk), k Є Z

7. cos x<0, x Є (π/2+2πk; 3π/2+2πk), k Є Z

8. Наибольшее значение, равное 1, y=cos x принимает в точках x= 2πk, k Є Z.

9. Наименьшее значение, равное -1, y=cos x принимает в точках x=π+ 2πk, k Є Z.

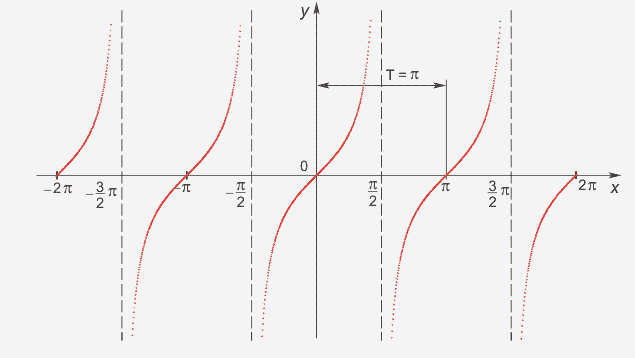
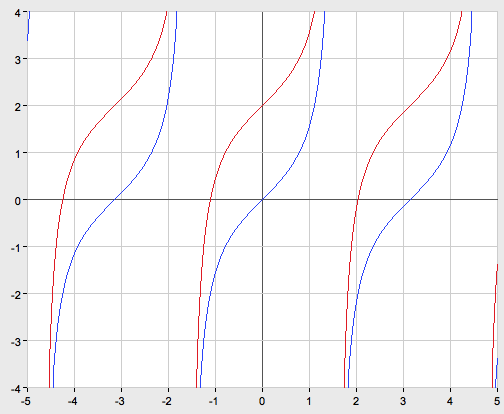
Cледующий график функции y=tg x (рис. 3)

Риc. 3

Свойства:

1. D(y)-множество всех действительных чисел, кроме чисел вида x=π/2 +πk, k Є Z

2. E(y)=(-∞;+ ∞), функция неограниченная

3. tg(-x)=-tg x, функция нечётная

4. наименьший положительный период: π
   tg(x+π)= tg x

5. tgx= 0 при x=πk, k Є Z

6. tg x> 0, x Є ( πk; π/2+πk), k Є Z

7. tg x< 0, x Є ( -π/2+πk; πk), k Є z

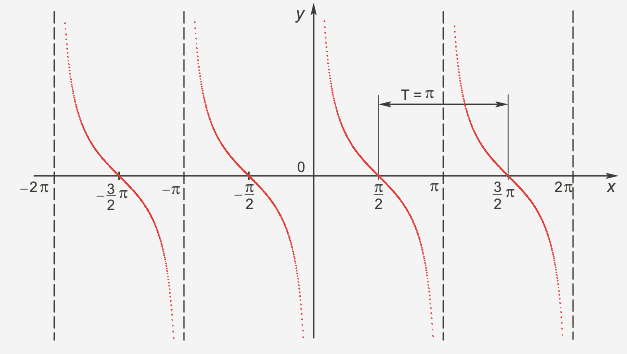
Следующий график функции y=ctg x (рис. 4)

Рис. 4

Свойства:

1. D(y)-множество всех действительных чисел, кроме чисел вида x=πk, k Є Z

2. E(y)= (-∞;+ ∞), функция неограниченная

3. ctg(-x)=-ctg x, функция нечётная

4. Наименьший положительный период: π
   ctg(x+π)=tg x

5. ctg x = 0 при x=π/2+πk, k Є Z

6. ctg x>0, x Є( πk; π/2+πk), k Є Z

7. ctg x<0, x Є( - π/2+πk; πk), k Є Z

Объяснение материала.

1. Для построения графика функции y=f(x)+a, где a — постоянное число, надо перенести график y=f(x) вдоль оси ординат. Если a>0, то график переносим параллельно самому себе вверх, если a < 0, то – вниз.

2. Для построения графика функции y=kf(x) надо растянуть график функции y=f(x) в k раз вдоль оси ординат. Если |k|>1, то происходит растяжение графика вдоль оси OY, если 0<|k|<1, то – сжатие.

3. График функции y=f(x+b) получается из графика y=f(x) путем параллельного переноса вдоль оси абсцисс. Если b>0 , то график перемещается влево, если b<0, то – вправо.

4. Для построения графика функции y=f(kx) надо растянуть график y=f(x) вдоль оси абсцисс. Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0<|k|<1 , то – растяжение.

Закрепление материала.

Уровень А

Частная дидактическая цель: отработать навык построения тригонометрических функций путем преобразований.

Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.

1.

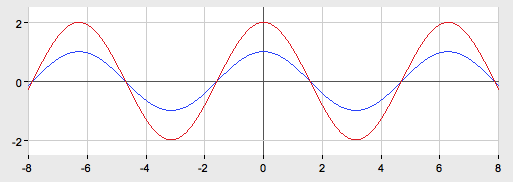
График функции 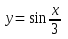получается из графика 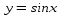путем растяжения вдоль оси Ox в 3 раза.

2.

График функции получается из графика 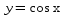путем растяжения вдоль оси Oy в 2 раза.

3.

График функции 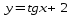получается из графика 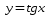путем параллельного переноса на 2 единицы вверх вдоль оси Oy.

4. 

График функции получается из графика путем параллельного переноса вдоль оси абсцисс на единиц влево.

5. 

Г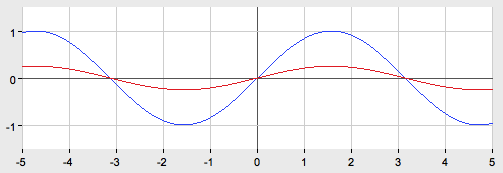
рафик функции 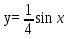получается из графика 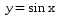путем сжатия вдоль оси Oy в 4 раза.

Уровень В.

Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.

Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.

1. 

График функции получается из графика 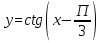путем параллельного переноса вдоль оси абсцисс на 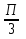единиц вправо.

2. 
   

График функции 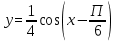получается из графика функции 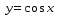путем последовательного выполнения следующих преобразований:

1) параллельный перенос на 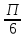единицы влево вдоль оси абсцисс

2) сжатие вдоль оси Оy в 4 раза.

3.

График функции 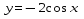получается из графика функции 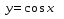, каждая ордината которого изменяется в -2 раза. Для этого выполняем следующие преобразования:

1) отображаем симметрично относительно оси Ox,

2) растягиваем в 2 раза вдоль оси Oy.

4.

График функции 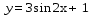получается из графика функции 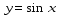последовательного выполнения следующих преобразований:

1) сжатие вдоль оси абсцисс в 2 раза;

2) растяжение в 3 раза вдоль оси Oy;

3) параллельный перенос на 1 единицу вверх вдоль оси ординат.

Уровень С.

Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.

Методический комментарий для учащихся: укажите, какие преобразования нужно выполнить для построения графиков. Постройте графики.

1.

График функции по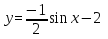лучается из графика функции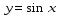путем последовательного выполнения следующих преобразований:

1) отображение симметрично относительно оси Ox,

2) сжатие в 2 раза вдоль оси Oy;

3) параллельный перенос на 2 единицы вниз вдоль оси Оy.

2.

График функции 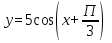получается из графика функции 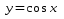последовательного выполнения следующих преобразований:

1) параллельный перенос вдоль оси абсцисс на 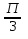единиц влево,

2) растяжение в 5 раза вдоль оси Oy.

3
.

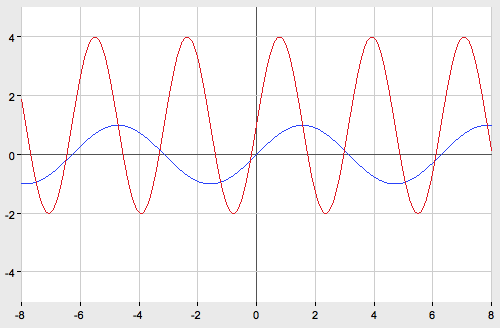
График функции 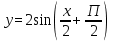получается из графика функции 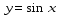последовательного выполнения следующих преобразований:

1) растяжение вдоль оси абсцисс в 2 раза;

2) параллельный перенос на 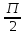единиц влево вдоль оси абсцисс.

3) растяжение в 2 раза вдоль оси Oy.

4.

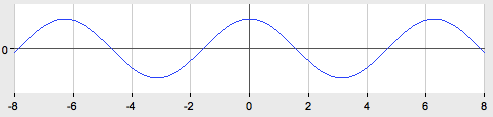
Так как cos (-x)=cos x, следовательно, y= cos x — чётная функция, значит, график функции тот же, что и график функции y= cos x.

5.

График функции 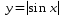получается из графика функции .Части графика функции , расположенные ниже оси абсцисс, зеркально отразятся и будут распо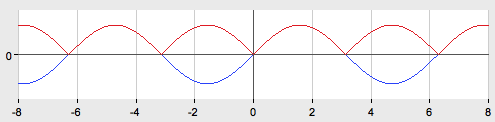
ложены в верхней полуплоскости.

Использованные ресурсы:

http://tvsh2004.narod.ru/alg07.html

http://www.aiportal.ru/services/graph.html