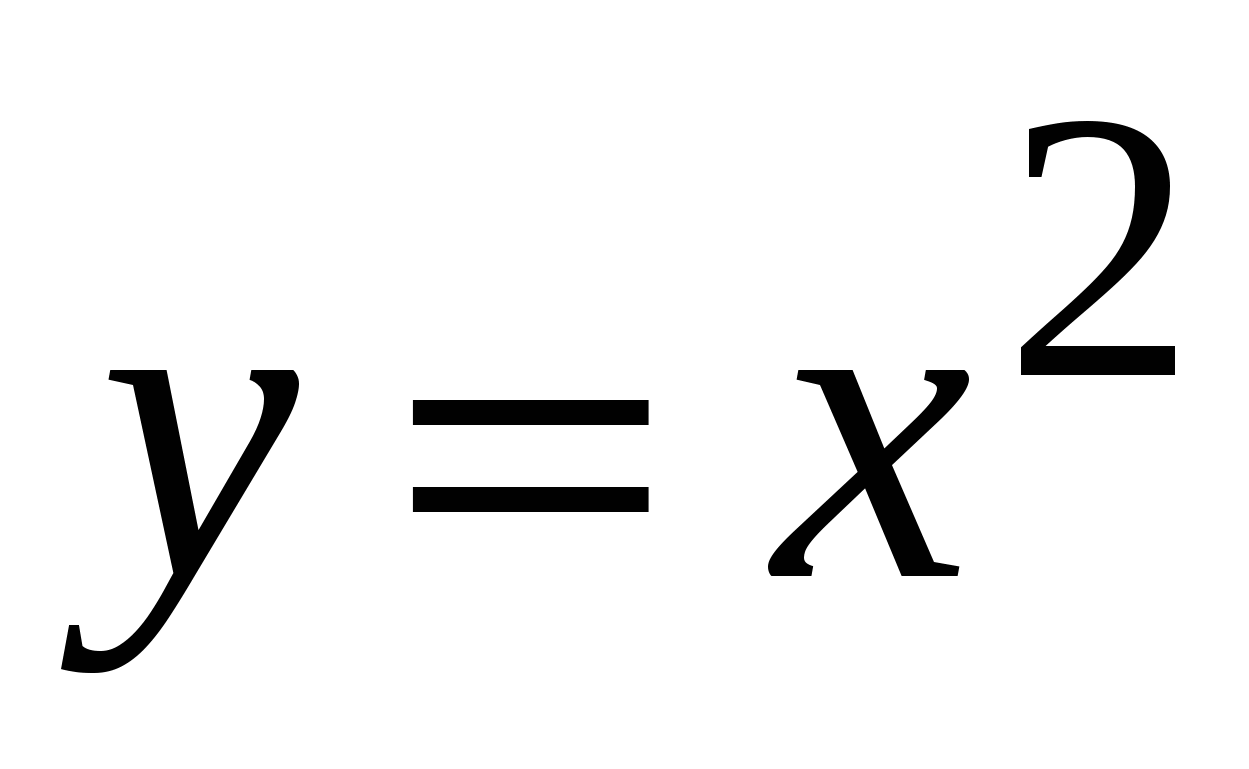Рабочая программа по алгебре в 7 классе

ГБОУ СОШ №2 «ОЦ» с. Кинель — Черкассы

Рабочая программа курса алгебры

(7 класс)

Автор: Сидоренко О. В.

учитель математики

Пояснительная записка

Статус документа

Настоящая программа по алгебре для основной общеобразовательной школы 7 класса составлена на основе Федерального государственного стандарта основного общего образования второго поколения, примерной программы общеобразовательных учреждений по математике 7–9 классы.

Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.

Цели изучения

Изучение математики в основной школе направлено на достижение следующих целей:

1. В направлении личностного развития:

• Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• Формирование качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• Развитие интереса к математическому творчеству и математических способностей;

2. В метапредметном направлении:

• Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3. В предметном направлении:

• Овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, для изучения смежных дисциплин, применения в повседневной жизни;

• Создание фундамента математического развития, формирования механизмов мышления, характерных для математической деятельности.

Место предмета в федеральном базисном учебном плане.

Базисный учебный (образовательный) план на изучение математики в 7 классе отводится 5 учебных часов в неделю, всего 175 часов, из них 105 часов на изучение алгебры и 70 часов – на изучение геометрии.

С учетом требований Федерального государственного образовательного стандарта основного общего образования в содержании рабочей программы предполагается реализовать компетентностный, личностно ориентированный и деятельностный подходы, которые определяют задачи обучения: приобретение математических знаний и умений; освоение универсальных учебных действий.

Компетентностный подход определяет следующие особенности предъявления содержания образования: оно представлено в виде трех тематических блоков, обеспечивающих формирование компетенций. В первом блоке представлены дидактические единицы, обеспечивающие совершенствование математических навыков. Во втором – дидактические единицы, которые содержат сведения из истории математики. Это содержание обучения является базой для развития коммуникативной компетенции учащихся. В третьем блоке представлены дидактические единицы, отражающие информационную компетенцию и обеспечивающие развитие учебно-познавательной и рефлексивной компетенций. Таким образом, рабочая программа обеспечивает взаимосвязанное развитие и совершенствование ключевых, общепредметных и предметных компетенций.

Принципы отбора содержания связаны с преемственностью целей образования на различных ступенях и уровнях обучения, логикой внутрипредметных связей, а также с возрастными особенностями развития учащихся.

Личностная ориентация образовательного процесса выявляет приоритет воспитательных и развивающих целей обучения. Способность учащихся понимать причины и логику развития математических процессов открывает возможность для осмысленного восприятия всего разнообразия мировоззренческих, социокультурных систем, существующих в современном мире. Система учебных занятий призвана способствовать развитию личностной самоидентификации, гуманитарной культуры школьников, их приобщению к естественно-математической культуре, усилению мотивации к социальному познанию и творчеству, воспитанию личностно и общественно востребованных качеств, в том числе гражданственности, толерантности.

Деятельностный подход отражает стратегию современной образовательной политики: необходимость воспитания человека и гражданина, интегрированного в современное ему общество, нацеленного на совершенствование этого общества. Система уроков сориентирована не столько на передачу готовых знаний, сколько на формирование активной личности, мотивированной к самообразованию, обладающей достаточными навыками и психологическими установками к самостоятельному поиску, отбору, анализу и использованию информации. Это поможет выпускнику адаптироваться в мире, где объем информации растет в геометрической прогрессии, где социальная и профессиональная успешность напрямую зависят от позитивного отношения к новациям, самостоятельности мышления и инициативности, от готовности проявлять творческий подход к делу, искать нестандартные способы решения проблем, конструктивно взаимодействовать с людьми.

Основой целеполагания является обновление требований к уровню подготовки выпускников в системе естественно-математического образования, отражающее важнейшую особенность педагогической концепции государственного стандарта – переход от суммы «предметных результатов» ( то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов), к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как универсальные учебные действия, что предполагает повышенное внимание к развитию межпредметных связей курса математики.

Дидактическая модель обучения и педагогические средства отражают модернизацию основ учебного процесса, их переориентацию на достижение конкретных результатов в виде сформированных регулятивных, коммуникативных и познавательных учебных умений. Формирование целостных представлений о математике будет осуществляться в ходе творческой деятельности учащихся на основе личностного осмысления математических фактов и явлений. Особое внимание уделяется познавательной активности учащихся, их мотивированности к самостоятельной учебной работе. Это предполагает все более широкое использование нетрадиционных форм уроков, в том числе методики деловых и ролевых игр, проблемных дискуссий, межпредметных интегрированных уроков и т.д.

Планируется использование следующих технологий в преподавании предмета:

• Технологии полного усвоения;

• Технологии обучения на основе решения задач;

• Технологии обучения на основе схематических и новых знаковых моделей.

Для естественно – математического образования приоритетным можно считать развитие умений самостоятельно и мотивированно организовывать свою познавательную деятельность, использовать элементы причинно-следственного и структурно-функционального анализа, определять сущностные характеристики изучаемого объекта, самостоятельно выбирать критерии для сравнения, сопоставления, оценки и классификации объектов – в программе это является основой для целеполагания.

На ступени основной школы задачи учебных занятий ( в схеме – планируемый результат) определены как закрепление умений разделять процессы на этапы, звенья, выделять характерные причинно – следственные связи, определять структуру объекта познания, значимые функциональные связи и отношения между частями целого, сравнивать, сопоставлять, классифицировать, ранжировать объекты по одному или нескольким предложенным основаниям, критериям. Принципиальное значение в рамках курса приобретает умение различать факты, мнения, доказательства, гипотезы, аксиомы.

При выполнении творческих работ формируется умение определять адекватные способы решения учебных задач на основе заданных алгоритмов, комбинировать известные алгоритмы деятельности в ситуациях, не предполагающих стандартного применения одного из них, мотивированно отказываться от образца деятельности, искать оригинальные решения.

Учащиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач, уметь формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять его с собственными математическими знаниями. Учащиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, рецензии.

Реализация рабочей программы обеспечивает освоение коммуникативных учебных действий, в том числе способностей передавать содержание текста в сжатом и развернутом виде в соответствии с целью учебного задания, проводить информационно-смысловой анализ текста, составлять план, тезисы, конспект. На уроках учащиеся более уверенно овладеют монологической и диалогической речью, умением вступать в речевое общение, участвовать в диалоге ( понимать точку зрения собеседника, признавать право на иное мнение), научатся приводить примеры, подбирать аргументы, перефразировать мысль, формулировать выводы. Для решения познавательных и коммуникативных задач учащимся предлагается использовать различные источники информации, включая энциклопедии, словари, Интернет-ресурсы и другие базы данных, в соответствии с коммуникативной задачей, сферой и ситуацией общения осознанно выбирать выразительные средства языка и знаковые системы.

В процессе обучения должно быть сформировано умение формулировать свои мировоззренческие взгляды как основа духовно-нравственного развития школьника.

Рабочая программа предусматривает обучение алгебре в 7 классах в объеме 102 часов, в неделю – 3 часа.

В том числе отводится для проведения:

• Контрольных работ – 9 учебных часов;

• Самостоятельных работ – 4 учебных часа;

• Проектной деятельности – 5 учебных часов;

• Исследовательской деятельности – 4 учебных часа.

С учетом уровневой специфики классов выстроена система учебных занятий, спроектированы цели, задачи, ожидаемые результаты обучения, что представлено в схематической форме ниже.

УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН

№

Тема	Кол-во часов	Кол-во контрольных работ
1	Глава 1. Математический язык. Математическая модель.	13	1
2.	Глава 2. Линейная функция.	15	1
3	Глава 3. Системы двух линейных уравнений с двумя неизвестными.	13	1
4	Глава 4. Степень с натуральным показателем и её свойства.	7	1
5	Глава 5. Одночлены. Арифметические операции над одночленами.	8	1
6	Глава 6. Многочлены. Арифметические операции над многочленами.	15	1
7	Глава 7. Разложение многочленов на множители.	18	1
8	Глава 8. Функция	9	1
9	Повторение	4	—

Содержание тем учебного курса

Математический язык. Математическая модель

Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.

Линейная функция

Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М (а; b) в прямоугольной системе координат.

Линейное уравнение с двумя переменными. Решение уравнения ах + by + с = 0. График уравнения. Алгоритм построения графика уравнения ах + by + с = 0.

Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции.

Линейная функция у = kx и ее график.

Взаимное расположение графиков линейных функций.

Системы двух линейных уравнений с двумя переменными (

Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения.

Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).

Степень с натуральным показателем

Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.

Одночлены. Операции над одночленами

Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены.

Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.

Многочлены. Арифметические операции над многочленами

Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена.

Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен.

Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов.

Деление многочлена на одночлен.

Разложение многочленов на множители

Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата.

Понятие алгебраической дроби. Сокращение алгебраической дроби.

Тождество. Тождественно равные выражения. Тождественные преобразования.

Функция у = х²

Функция у = х², ее свойства и график. Функция у = — х², ее свойства и график.

Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Разъяснение смысла записи у = f(x). Функциональная символика.

Требования к уровню подготовки учащихся 7 классов

(базовый уровень)

В результате изучения математики ученик должен

Знать/понимать: математический язык; свойства степени с натуральным показателем; определение одночлена и многочлена, операции над одночленами и многочленами; формулы сокращенного умножения; способы разложения многочлена на множители; линейную функцию, ее свойства и график; квадратичную функцию и ее график; способы решения системы двух линейных уравнений с двумя переменными;

Уметь: составлять математическую модель при решении задач; выполнять действия над степенями с натуральными показателями, показателем, равным нулю используя свойства степеней; выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения; сокращать алгебраические дроби; строить графики линейной и квадратичной функций; решать системы двух линейных уравнений с двумя переменными;

Владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;

Быть способным решать следующие жизненно-практические задачи: самостоятельно приобретать и применять знания в различных ситуациях, работать в группе, аргументировать и отстаивать свою точку зрения, уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов; пользоваться предметным указателем, энциклопедией и справочником для нахождения информации; самостоятельно действовать в ситуации неопределенности при решении актуальных для учащихся проблем.

Литература

Настоящая рабочая программа разработана применительно к учебной программе А. Г. Мордковича «Алгебра» для 7-9 классов и ориентирована на использование учебно-методического комплекта:

1. Алгебра. 7-9 классы: рабочие программы по учебникам А.Г. Мордковича, П.В. Семенова /авт. – сост. Н.А. Ким, Н.И. Мазурова – Волгоград: Учитель, 2011

2. Александрова, Л. А. Алгебра. 7 класс: контрольные работы / Л. А. Александрова; под редакцией А. Г. Мордковича.- М.: Мнемозина, 2010

3. Александрова, Л. А. Алгебра. 7 класс: самостоятельные работы / Л. А. Александрова; под редакцией А. Г. Мордковича.- М.: Мнемозина, 2010

4. Арутюнян, Е. Б. Математические диктанты для 5 – 9 классов / Е. Б. Арутюнян. – М.: Просвещение, 2007

5. Дудницын, Ю. Алгебра. Карточки с заданиями для 7 класса / Ю. Дудницын, В. Кронгауз. – М.: Просвещение, 2007

6. Кострикина, Н. П. Задачи повышенной трудности в курсе алгебры 7 – 9 классов/ Н. П. Кострикина. – М.: Просвещение, 2007

7. Мордкович, А. Г. Алгебра. 7 класс: в 2 ч. Ч.1: учебник для учащихся общеобразовательных учреждений/ А. Г. Мордкович.- М.: Мнемозина, 2010

8. Мордкович, А. Г. Алгебра. 7 класс: в 2 ч. Ч.2: задачник для учащихся общеобразовательных учреждений/ А. Г. Мордкович (и др.); — М.: Мнемозина, 2010

9. Мордкович, А. Г. Алгебра. 7 класс: методическое пособие для учителя / А. Г. Мордкович.- М.: Мнемозина, 2010

10. Мордкович, А. Г. Алгебра. 7-9 классы: тесты / А. Г. Мордкович, Е. Е. Тульчинская — М.: Мнемозина, 2011

11. Программа. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа.10-11 классы. Авт. – сост. И. И. Зубарева, А.Г. Мордкович.: Мнемозина, 2011

Дополнительная литература для учителя:

12. Арутюнян, Е. Б. Математические диктанты для 5 – 9 классов / Е. Б. Арутюнян. – М.: Просвещение, 2007

13. Кострикина, Н. П. Задачи повышенной трудности в курсе алгебры 7 – 9 классов/ Н. П. Кострикина. – М.: Просвещение, 2007

14. Дудницын, Ю. Алгебра. Карточки с заданиями для 7 класса / Ю. Дудницын, В. Кронгауз. – М.: Просвещение, 2007

Информационно-методическое обеспечение учебного процесса

1. Дополнительная литература для учащихся.

1. Мантуленко, В. Г. Математика: кроссворды для школьников/ В. Г. Мантуленко, О. Г. Гетманенко. – Ярославль: Академия развития, 2004

2. Пичурин, Л. Ф. За страницами учебника алгебры: книга для учащихся 7-9 классов средней школы/ Л. Ф. Пичурин. – М.: Просвещение, 1990

3. Черкасов, О. Ю. Математика: справочник для старшеклассников и поступающих в вузы/ О. Ю. Черкасов, А. Г. Якушев. – М.: АСТ-Пресс Школа, 2006.

4. Энциклопедия для детей. Т.11. Математика/ под ред. М Аксеновой. – М.: Аванта+, 2007

5. Я познаю мир. Великие ученые: энциклопедия. – М.: АСТ: Астрель: Ермак, 2004

6. Я познаю мир. Математика: энциклопедия. – М.: АСТ: Астрель: Хранитель: Харвест, 2007

2. Цифровые образовательные ресурсы ( ЦОР).

1. Министерство образования РФ.- Режим доступа: http://www.informika.ru; http://www.ed.gov.ru; http://www.edu.ru

2. Тестирование online: 5-11 классы. – Режим доступа: http://www.kokch.kts.ru/cdo

3. Педагогическая мастерская, уроки в Интернет и многое другое. – Режим доступа: http://teacher.fio.ru

4. Новые технологии в образовании. – Режим доступа: http://edu.secna.ru/main

5. Путеводитель «В мире науки» для школьников. – Режим доступа: http://www.uic.ssu.samara.ru/~nauka

6. Мегаэнциклопедия Кирилла и Мефодия. – Режим доступа: http://mega.km.ru

7. Сайты энциклопедий, например, — Режим доступа: http://www.rubricon.ru ; http://www.encyclopedia.ru

8. Единая коллекция цифровых образовательных ресурсов по математике. – Режим доступа: http://school—collection.edu.ru/collection

Тема раздела: Математический язык. Математическая модель. (13 часов)

Цели:

• формирование представлений о целостности и непрерывности курса математики 5-6 классов;

• обобщение и систематизация знаний о числовых выражениях, допустимых и недопустимых значениях переменной выражения, математических утверждениях, математическом языке; выполнении действий по ариф. законам сложения и умножения, действий с десятичными дробями, действий с обыкновенными дробями;

• овладение навыками решения задач, составляя математическую модель реальной ситуации;

• развитие логического, математического мышления и интуиции, творческих способностей в области математики.

№

Тема	Кол – во часов	Дата	Планируемые результаты		Основные понятия
			Предметные	Метапредметные
1	Числовые и буквенные выражения	3		Уметь находить значение алгебраического выражения при заданных значениях переменных; определять значения переменных, при которых выражение имеет смысл.	Уметь излагать информацию, интерпретируя факты, разъясняя значение и смысл теории, воспринимать устную речь, приводить и разбирать примеры.	Числовые выражения, значение числового выражения, значение алгебраического выражения, допустимые и недопустимые значения переменной, алгебраические выражения, порядок выполнения действий, арифметические законы сложения и умножения, действия с десятичными дробями, действия с обыкновенными дробями
2	Математический язык	2		Знать понятие математического языка. Уметь осуществлять «перевод» выражений с математического языка на обычный и обратно.	Уметь излагать свои мысли ясно, грамотно; понимать смысл поставленной задачи.	Математическое буквенное выражение, математическое утверждение, математический язык.
3	Математическая модель	2		Уметь составлять математическую модель реальной ситуации, используя математический язык, решать текстовые задачи, выделяя три этапа математического моделирования.	Уметь видеть математическую задачу в контексте проблемной ситуации.	Математическая модель, реальные ситуации, словесная модель, алгебраическая модель, графическая модель, ге6ометрическая модель.
4	Линейное уравнение с одной переменной.	2		Уметь решать линейные уравнения с одной переменной.	Уметь работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; решать проблемные задачи и ситуации	Линейное уравнение с одной переменной, переменная, корни уравнения.
5	Координатная прямая.	3		Уметь связывать геометрическую и аналитическую модели числового промежутка, выбирать обозначение и символическую запись	Уметь составлять алгоритмы, отражать результаты деятельности в письменной форме.	Координатная прямая, координата точки, числовой промежуток, интервал, полуинтервал, отрезок, открытый луч, луч
6	Контрольная работа №1 «Математический язык. Математическая модель».	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Линейная функция. (15 часов) Цели: формирование представлений о прямоугольной системе координат, об абсциссе, ординате, о числовых промежутках, числовых лучах, линейной функции и её графике; формирование умений построения графика линейной функции, исследования взаимного расположения графиков линейных функций; овладение умением применения алгоритма отыскания координат точки, заданной в прямоугольной системе координат, алгоритма построения точки в прямоугольной системе координат, алгоритма построения графика линейного уравнения ах+ву+с=0; овладение навыками решения линейного уравнения с двумя переменными ах+ву+с=0.
7	Координатная плоскость.	2		Уметь пользоваться алгоритмами нахождения координат точки на плоскости и отыскания точки по её координатам.	Умение аргументировано отвечать на поставленные вопросы, проводить самооценку собственных действий.	Прямоугольная система координат. Алгоритм нахождения координат точки на плоскости и отыскание точки по её координатам
8	Линейное уравнение с двумя переменными.	7		Уметь строить график линейного уравнения с двумя переменными по алгоритму	Умение аргументировано отвечать на поставленные вопросы, проводить самооценку собственных действий.	Линейное уравнение с двумя переменными. Алгоритм построения графика линейного уравнения ах+ву+с=0
9	Линейная функция	3		Уметь строить и читать график функции у=кх+в	Уметь объяснить изученные положения на самостоятельно подобранных конкретных примерах.	Линейная функция. График линейной функции. Наибольшее и наименьшее значения линейной функции. Возрастание и убывание.
10	Взаимное расположение графиков линейных функция.	2		Уметь определять взаимное расположение графиков линейных функций	Уметь работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; решать проблемные задачи и ситуации.	Взаимное расположение графиков линейных функций.
11	Контрольная работа №2 по теме «Линейная функция».	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Системы двух линейных уравнений с двумя неизвестными.( 13 часов) Цели: формирование представлений о системе двух линейных уравнений с двумя переменными, о несовместимости системы, о неопределенной системе уравнений; овладение умением решения систем линейных уравнений графическим методом, методом подстановки и методом алгебраического сложения; овладение навыками составления математической модели реальных событий в виде системы двух линейных уравнений с двумя переменными.
12	. Основные понятия.	2		Уметь решать системы уравнений графическим методом	Умение понимать и использовать математические средства наглядности для аргументации выводов	Система уравнений. Решение системы уравнений. Графический метод решения систем уравнений
13	Метод подстановки	2		Уметь решать системы уравнений методом подстановки	Умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки.	Метод подстановки. Алгоритм решения систем уравнений методом подстановки
14	Метод алгебраического сложения	4		Уметь решать системы уравнений методом сложения	Уметь аргументировано отвечать, приводить примеры	Алгоритм решения систем уравнений методом алгебраического сложения
15	Системы линейных уравнений с двумя переменными как математические модели реальных ситуаций.	4			Воспроизводить прочитанную информацию с заданной степенью свернутости; правильно оформлять решения; выбирать из данной информации нужную информацию.
16	Контрольная работа №3 по теме «Системы линейных уравнений с двумя переменными».	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Степень с натуральным показателем и её свойства. ( 7 часов) Цели: формирование представлений о степени с натуральным показателем, о степени с нулевым показателем; формирование умений составления таблицы основных степеней и её применение при решении заданий; овладение умением применения свойств степени с натуральным показателем при решении задач, выполнять действие умножения пи деления степеней с одинаковыми показателями; овладение навыками решения уравнений, содержащих степень с нулевым показателем.
17	Что такое степень с натуральным показателем	1		Уметь: возводить числа в степень, заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц.	Уметь работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; решать проблемные задачи и ситуации	Степень с натуральным показателем, степень, основание степени, показатель степени, возведение в степень, четная степень, нечётная степень.
18	Таблица основных степеней.	1		Уметь:пользоваться таблицей степеней при выполнении вычислений со степенями.	Уметь определять понятия, приводить доказательства.	Степени числа 2, степени числа 3, степени числа 5, степени числа 7, степени составных чисел.
19	Свойства степени с натуральным показателем.	2		Уметь применять свойства степени для упрощения числовых и алгебраических выражений.	Умение понимать и использовать математические средства наглядности для аргументации выводов	Свойства степеней, доказательство свойств степеней, теорема, условие, заключение.
20	Умножение и деление степеней с одинаковым показателем	2		Знать правила умножения и деления степени с одинаковыми показателями; как применять эти правила при вычислениях, для преобразования алгебраических выражений.	Уметь аргументировано отвечать, приводить примеры	Степень с разными основаниями, действия со степенями одинакового показателя
21	Контрольная работа №4по теме «Степень с натуральным показателем»	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Одночлены. Операции над одночленами. ( 8 часов) Цели: формирование представлений об одночлене стандартного вида, об арифметических операциях над одночленами, о подобных одночленах; формирование умений представлять одночлен в стандартном виде, выполнять арифметические действия над одночленами; овладение умением складывать, вычитать, умножать и делить одночлены, а также возводить одночлен в степень.
22	Понятие одночлена. Стандартный вид одночлена.	1		Уметь находить значение одночлена при указанных значениях переменных	Уметь работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; решать проблемные задачи и ситуации	Одночлен, стандартный одночлен, коэффициент одночлена.
23	Сложение и вычитание одночленов.	2		Уметь применять правила сложения и вычитания одночленов для упрощения выражений и решения уравнений.	Уметь работать по заданному алгоритму, доказывать правильность решения с помощью аргументов; решать проблемные задачи и ситуации	Подобные одночлены, метод введения новой переменной, алгоритм сложения (вычитания) одночленов.
24	Умножение одночленов. Возведение одночлена в натуральную степень.	2		Уметь применять правила умножения одночленов, возведения одночлена в степень для упрощения выражений.	Работать по заданному алгоритму, выделять и записывать главное.	Умножение одночленов, возведение одночлена в натуральную степень, корректная задача, некорректная задача.
25	Деление одночлена на одночлен.	2		Уметь выполнять деление одночленов по алгоритму, применять правило деления одночленов для упрощения алгебраических дробей.		Деление одночлена на одночлен, стандартный вид делителя и делимого, алгоритм деления одночлена на одночлен.
26	Контрольная работа №4 по теме «Одночлены. Действия над одночленами».	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Многочлены. Операции над многочленами. ( 15 часов) Цели: формирование представлений о многочлене, о приведении подобных членов многочлена, о стандартном виде многочлена, о формулах сокращенного умножения; формирование умений представлять многочлен в стандартном виде, выполнять арифметические действия над многочленом; овладение умением складывать, вычитать, умножать и делить многочлены, выводить и применять формулу сокращенного умножения.
27	Основные понятия.	1		Иметь представление о многочлене, о действии приведения подобных членов многочлена, о стандартном виде многочлена, о полиноме. Уметь выбрать и выполнить задание по своим силам.	Уметь приводить примеры; аргументировать ответ, формулировать выводы.	Многочлен, члены многочлена, приведение подобных членов, стандартный вид многочлена, полином.
28	Сложение и вычитание многочленов.	2		Знать правило составления алгебраической суммы многочленов. Уметь выполнять сложение и вычитание многочленов.	Умение аргументировано отвечать на поставленные вопросы, проводить самооценку собственных действий.	Сложение и вычитание многочленов, взаимное уничтожение слагаемых, алгебраическая сумма многочленов, правила составления алгебраической суммы многочленов.
29	. Умножение многочлена на одночлен	2		Уметь выполнять умножение многочлена на одночлен, выносить общий одночленный множитель за скобки.	Уметь воспроизводить изученную информацию с заданной степенью свернутости, работать по заданному алгоритму и правильно оформлять работу	Умножение многочлена на одночлен, распределительный закон умножения, вынесение общего множителя за скобки.
30	Умножение многочлена на многочлен	2		Уметь выполнять умножение многочленов. Уметь решать текстовые задачи, математическая модель которых содержит произведение многочленов.	Умение ставить цели, выбирать и создавать алгоритмы для решения математических и практических задач.	Раскрытие скобок, умножение многочлена на многочлен.
31	Формулы сокращенного умножения.	5		Уметь выполнять преобразования многочленов, вычисления по формулам сокращенного умножения.	Уметь воспроизводить изученную информацию с заданной степенью свернутости, работать по заданному алгоритму и правильно оформлять работу	Квадрат суммы, квадрат разности, разность квадратов, разность кубов, сумма кубов.
32	Деление многочлена на одночлен.	1		Уметь использовать правило деления многочлена на одночлен для упрощения выражений, решения уравнений, отражать свои решения в письменной форме.	Умение аргументировано отвечать на поставленные вопросы, проводить самооценку собственных действий	Свойство деления суммы на число, правило деления многочлена на одночлен.
33	Контрольная работа №5 по теме «Многочлены»	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Разложение многочленов на множители. ( 18 часов) Цели: формирование представлений о разложении многочлена на множители, об алгебраической дроби, о тождествах; формирование умений вынесения множителя за скобки, группировки слагаемых, преобразования выражений с использованием формулы сокращенного умножения, выделения полного квадрата; овладение навыками решения уравнений, выделения полного квадрата, решения уравнений с применением формул сокращенного умножения.
34	Что такое разложение многочленов на множители и зачем оно нужно.	1		Иметь представление о корнях уравнения, о сокращении дробей, о разложении многочлена на множители.	Уметь подбирать аргументы для доказательства своей точки зрения.	Разложение на множители, корни уравнения, сокращение дробей, разложение многочлена на множители
35	Вынесение общего множителя за скобки	2		Уметь применять приём вынесения общего множителя за скобки для упрощения вычислений, решения уравнений; рассуждать, обобщать, находить несколько решений одной задачи.	Уметь воспроизводить изученную информацию с заданной степенью свернутости, работать по заданному алгоритму и правильно оформлять работу	Вынесение общего множителя за скобки, НОД коэффициентов, алгоритм отыскания общего множителя нескольких одночленов.
36	. Способ группировки.	2		Уметь выполнять разложение многочлена на множители способом группировки по алгоритму.	Уметь аргументировано рассуждать, обобщать.	Способ группировки, разложение на множители.
37	Разложение многочлена на множители с помощью формул сокращённого умножения	5		Уметь применять приём разложения многочлена на множители с помощью формул сокращённого умножения для упрощения вычислений и решения уравнений.	Воспринимать устную речь, проводить информационно-смысловой анализ.	Формулы сокращенного умножения, разложение на множители по формулам сокращённого умножения.
38	Разложение многочлена на множители с помощью комбинации различных приёмов.	3		Уметь выполнять разложение многочлена на множители с помощью комбинированных приёмов: вынесение за скобки общего множителя, формулы сокращённого умножения, способ группировки, метод выделения полного	Уметь подбирать аргументы для доказательства своей точки зрения.	Комбинации различных приемов. Метод выделения полного квадрата.
39	Контрольная работа №6 по теме «Разложение многочлена на множители».	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
40	Сокращение алгебраических дробей.	3		Уметь применять различные способы разложения многочлена на множители при сокращении алгебраических дробей дробей	Уметь рассуждать, обобщать, систематизировать.	Алгебраическая дробь, числитель алгебраической дроби, знаменатель алгебраической дроби, сокращение алгебраической дроби.
41	Тождества.	1		Уметь пользоваться основными алгоритмическими приемами доказательства тождества	Работать по заданному алгоритму, выделять и записывать главное.	Тождества. Доказательство тождества
Тема раздела: Функция у=х² (9 часов)
42	. Функция у=х² и её график.	3		Уметь строить и читать график функцииу=х2	Умение использовать функционально-графические представления для иллюстрации  и описания реальных зависимостей.	Парабола, её элементы. функция у=х
43	Графическое решение уравнений.	2		Уметь решать уравнения графическим способом	Умение использовать функционально-графические представления для иллюстрации  и описания реальных зависимостей.	Графическое решение уравнений. Алгоритм графического решения уравнений.
44	Что означает в математике запись у=f(х).	2		Знать функциональную символику, читать графики	Умение использовать функционально-графические представления для иллюстрации  и описания реальных зависимостей.	Смысл записи у=f(х), кусочная функция, область определения функции, непрерывность функции
45	Контрольная работа №7 по теме «Функция»	1		Уметь обобщать и систематизировать знания по теме	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
Тема раздела: Повторение. ( 4 часа) Цели: обобщение и систематизация курса алгебры 7 класса; создание условий для плодотворного участия каждого ученика в работе группы; умения самостоятельно  и мотивированно организовывать свою деятельность.
46	Итоговое повторение. Степень с натуральным показателем и её свойства.	1		Уметь обобщать и систематизировать знания за курс 7 класса.	Умение самостоятельно и мотивированно организовать свою познавательную деятельность (от постановки цели до получения результатов).
47	Итоговое повторение. Разложение многочлена на множители.	1
48	Итоговое повторение. Функция у=х² и её график	1
49	Итоговое повторение. Системы двух линейных уравнений с двумя переменными.	1