| III. Изучение нового материала. ( слайд № 3 — 16) Геометрия — одна из наиболее древних наук. Первые геометрические факты найдены в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до нашей эры), а также в других источниках. Название науки «геометрия» древне греческого происхождения, оно составлено из двух древнегреческих слов: «ge» — «земля» и «metreo» — «измеряю» (землю измеряю). Появление и развитие геометрических знаний связано с практической деятельностью людей. Это отразилось и в названиях многих геометрических фигур. Например, название фигуры трапеция происходит от греческого слова trapezion — «столик», от которого произошло также слово «трапеза». Термин линия возник от латинского linum — «лен, льняная нить». Практические потребности людей (сооружение жилищ, храмов, желание украсить одежду, рисовать картины) способствовали приобретению и накоплению геометрических сведений, которые изначально передавались в устной форме и поколения в поколение. Новые сведения и факты добывались опытным путем, выводились некоторые правила (например, правило вычисления площадей) и данная наука не являлась точной. И только в VI веке до нашей эры древнегреческий ученый Фалес начал получать новые геометрические сведения с помощью доказательств. В III веке до нашей эры греческий ученый Евклид написал сочинение «Начала» и почти два тысячелетия геометрия изучалась по этой книге, а наука в честь ученого была названа евклидовой геометрией. В настоящее время геометрия — это целая наука, занимающаяся изучением геометрических фигур. Какие геометрические фигуры вам известны? прямая ломаная отрезок луч прямоугольник квадрат многоугольник куб цилиндр шар конус пирамида параллелепипед | По какому принципу данные геометрические фигуры записаны в двух различных группах? (В первой группе записаны фигуры, существующие на плоскости, а во второй группе фигуры, существующие в пространстве). Часть геометрии, в которой рассматриваются фигуры на плоскости, называется планиметрией, а та часть, в которой рассматриваются фигуры в пространстве, называется стереометрией. Мы начнем изучение геометрии с планиметрии. Выполним следующие упражнения. (Выполняются следующие упражнения, при этом вводятся новые понятия и определения.) ( слайд № 10) 1. Начертите прямую. Как её можно обозначить? (Прямая а или AB, см. рис. 1) 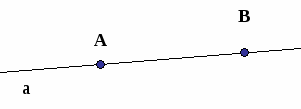 рис. 1 2.Отметьте точку С, не лежащую на данной прямой и точки D, Е, К, лежащие на этой же прямой. (Рис. 2) 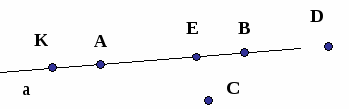 рис. 2 В математике существуют специальные символы, позволяющие кратко записать какое — либо утверждение. Символы ∈ и ∉ означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности. Используя символы принадлежности запишем. K ∈ a, или K ∈ AB, E ∈ a, или E ∈ AB, D ∈ a, или D ∈ AB, C ∉ a, или C ∉ AB. Можно сказать, что прямая a проходит через точки А, K, B, E, D, но не проходит через точку C. 3. ( слайд № 11)Используя символы принадлежности, запишите предложение. Точка D принадлежит прямой АВ, а точка С не принадлежит прямой a. (D ∈ АВ, С ∉ а.)  C 4. Используя рисунок и символы ∈ и ∉ , запишите, какие точки принадлежат прямой b, а какие — нет. A E B  F    b  N K   F ∈ b, В ∈ b, А ∈ b, С ∈ b;K ∉ b,E ∉ b,N ∉ b. Сколько прямых можно провести через заданную точку А? ( слайд № 12)Через любые две точки можно провести прямую? Сколько прямых можно провести через две точки? Итак, через любые две точки провести прямую и притом только одну. Это утверждение назовём свойством прямой. 5. ( слайд № 13) Начертите прямые XY и МК, пересекающиеся в точке О. Для того, чтобы кратко записать, что прямые XY и МК пересекаются в точке О, используют символ ∩ и записывают так: XY ∩ MK=O. Символ ∩ означает пересечение. Сколько общих точек может быть у двух прямых? Сколько общих точек может быть у двух прямых? Таким образом, две прямые либо имеют только одну общую точку, либо не имеют общих точек.  6. ( слайд № 14)На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки. 6. ( слайд № 14)На прямой а отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки. (отрезки АВ, ВС, CD, AC, AD, BD.) Отрезок – часть прямой, ограниченная двумя точками 7. ( слайд № 15)Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М. а) являются ли прямые MN и а различными прямыми? б) может ли прямая b проходить через точку N? ( слайд № 16)Рассмотрим прием «проведения» длинных отрезков прямых на местности. Этот прием заключается в следующем. Сначала отмечают какие-нибудь точки A и В. Для этой цели используют две вехи — шесты длиной около 2 м, заостренные на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху ставят так, чтобы вехи, стоящие в точках A и В, закрывали ее от наблюдателя, находящегося в точке A. Следующую веху ставят так, чтобы ее закрывали вехи, стоящие в точках В и С, и т. д. Ясно, что таким способом можно построить сколь угодно длинный отрезок прямой. Описанный прием называется провешиванием прямой (от слова «веха»). Он широко используется на практике, например при рубке лесных просек, при прокладывании трассы шоссейной или железной дороги, линий высоковольтных передач и т. д. | 12 | Объясняет, используя презентацию. | Внимательно слушают объяснение учителя. Выполняют письменно упражнения(на доске и в тетрадях),отвечают на вопросы учителя. |
| IV Формирование умений и навыков учащихся №2. ( слайд № 18) Отметьте три точки A, B и C, не лежащие на одной прямой,проведите прямые AB, BC и CA. №5. ( слайды № 19 — 23) Проведите прямую а и отметьте на ней точки A и B. Отметьте: а) Точки M и N, лежащие на отрезке AB; б) Точки P и Q, лежащие на прямой a, но не лежащие на отрезке AB; в) Точки R и S, не лежащие на прямой a. №7. ( слайд № 26) На рисунке изображена прямая, на ней отмечены точки A, B,C и D. Назовите все отрезки: а) на которых лежит точка С;б) на которых не лежит точка B;  Дополнительные задания( слайд № 17),решение слайды № 24-25. 1. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки. 2. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки. V.Физминутка( слайды № 26 — 27) -
Исходное положение – стоя, руки в стороны. Сжимая и разжимая ладошки дети изображают прямые, отрезки и лучи. -
Исходное положение – сидя. Если они считают, что предложение истинное, то встают, руки вперед. Иначе – встают, руки вверх. VI. Самостоятельная работа.(на карточках) Вариант I. С—1 (Рис. 1) -
Пересекаются ли отрезки АВ и CD? -
Пересекаются ли прямые АВ и CD? -
Отметьте точку М так, чтобы она лежала на прямой CD, но не лежала ни на отрезке АВ, ни на отрезке CD. -
Отметьте точку N, которая лежит на прямой CD между точками А и В. Как вы назовете такую точку?   
L F Рис. 1 
E K Рис. 2 Вариант II. С—1 () 1. Пересекает ли прямая КL отрезок ЕF? 2. Пересекает ли прямая КL прямую ЕF? 3. Отметьте точку А, которая лежит на прямой Е, но не лежит на прямой КL. 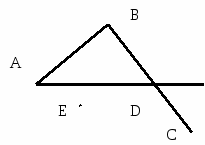 4. Существуют ли точки, которые одновременно лежат на отрезке ЕF и прямой LК? 4. Существуют ли точки, которые одновременно лежат на отрезке ЕF и прямой LК?
Рис. 3 Вариант III. С—1 (Рис. 3) 1. Сколько существует различных отрезков с концами в точках А, В, С и D? 2. Пересекаются ли прямые АВ и СD? З. Какая из точек, А или В, лежит между точками В и С? 4. Отметьте точку М, которая лежит на прямой АВ, но не лежит на отрезке ВС. 5. Проведите прямую, проходящую через точку Е, которая пересекает прямые АВ и ВС, но не пересекает отрезок АD. Вариант IV. С—1 (Рис. 71) -
Сколько существует различных отрезков с концами в точках Е, F, М и N? -
Пересекаются ли прямые ЕN и FМ? -
Какая из точек, А или N, лежит между точками Е и F? -
Отметьте точку В, которая лежит на отрезке МN, но не лежит на прямой ЕF 5. Проведите прямую, проходящую через точку А, которая пересекает прямые ЕF и МN, но не пересекает отрезок FМ 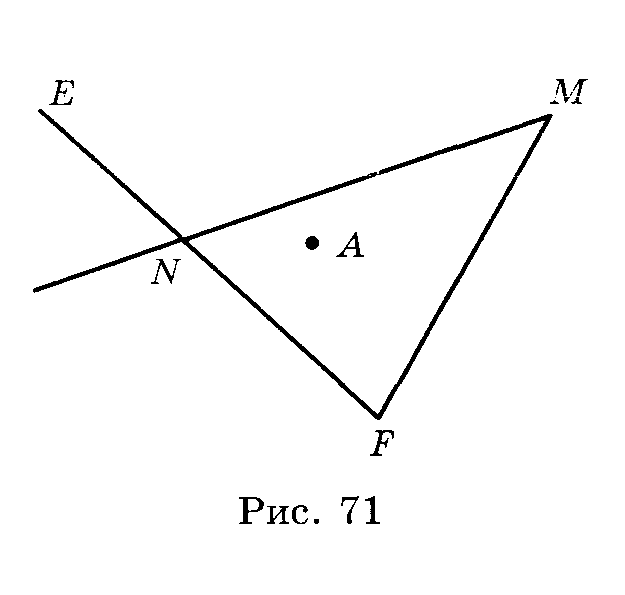
| 12 1 7 | Следит за верностью рассуждений учащихся. Демонстрирует на слайдах верное решение. | Решают самостоятельно, делая записи в тетради. Проверяют верно ли они решили задачи. Самостоятельно решают задачи. |

















