Конспект урока геометрии для 7 класса на тему « Треугольники. Признаки равенства треугольников»

Конспект урока геометрии для 7 класса на тему

« Треугольники.

Признаки равенства треугольников»

Цели урока:

Образовательные:

— закрепить, обобщить и систематизировать материал по теме «Треугольники. Признаки равенства треугольников»;

— отработка навыков построения треугольников по трем элементам;

— расширить и углубить знания, умения учащихся;

— научить применять полученные знания при выполнении практических заданий с переходом на более высокий уровень.

Развивающие:

— способствовать развитию наблюдательности, умению анализировать, сравнивать и делать выводы;

— развивать познавательные интересы, память, внимание и сообразительность;

— развитие логического мышления, математической речи, интереса учащихся к изучению геометрии;

— формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения.

Воспитательные:

— повысить интерес учащихся к нестандартным задачам;

— знакомство с биографическими данными Николая Ивановича Лобачевского;

— способствовать формированию активности.

Тип урока: урок обобщения и систематизации знаний, умений и навыков

Ход урока:

1. Организационный момент.

Учитель: В геометрии среди множества различных фигур на плоскости выделяется большое семейство многоугольников. Ребята, вслушайтесь, как звучит слово «многоугольники» и ответьте на вопрос: «Из каких слов оно состоит?»

( Слово многоугольник состоит из двух слов: «много» и «угольник».)

( слайд 2)

Учитель: Каким наименьшим числом можно заменить слово «много» в этом слове?

(Слово «много» можно заменить наименьшим числом «три».)

Учитель: Какое слово получим?

(Мы получим слово «треугольник».)

Учитель: Значит самым «простым» многоугольником является треугольник. Но «простым» ли он является нас самом деле? Вот в этом мы и должны с вами сегодня разобраться.

Ребята, кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолеты. Если вы решите отыскать его на географической карте, он находится в Атлантическом океан между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида.

(слайд 3)

Однако знакомый нам с детства треугольник также таит в себе немало интересного и загадочного.

Сегодня на уроке мы с вами вспомним все известное об этой фигуре. Вспомним виды треугольников, их свойства; понятия «биссектриса», «медиана», «высота», вертикальные и смежные углы и их свойства; признаки равенства треугольников и построение треугольника по трем элементам. Кроме, того познакомимся с некоторыми фактами, не известными ранее.

2.Устная работа.

Учитель: Ребята, вспомним виды треугольников и их отличительные особенности. Ответьте на следующие вопросы:

1. На какие группы в зависимости от длин сторон можно разделить все треугольников?

(В зависимости от длин сторон можно треугольники можно разделить на три группы: разносторонние, равнобедренные, равносторонние или правильные)

2. Какими свойствами характеризуются треугольники каждой из этих групп? Дайте определения.

(Треугольник, у которого все стороны различные, называется разносторонним. Треугольник, у которого две стороны равны, называется равнобедренный. Треугольник, у которого все стороны равны, называется равносторонним.)

Учитель: Ребята, а что можно сказать об углах равностороннего треугольника.

( углы равностороннего треугольника равны между собой)

Учитель: запомните это свойство. Оно сегодня на уроке нам пригодится. А теперь вспомним признаки равенства треугольников.

1. На рисунке ОД – биссектриса < АОВ,

ДО – биссектриса < АДВ. Доказать: ОА = ОВ

ДА = ДВ

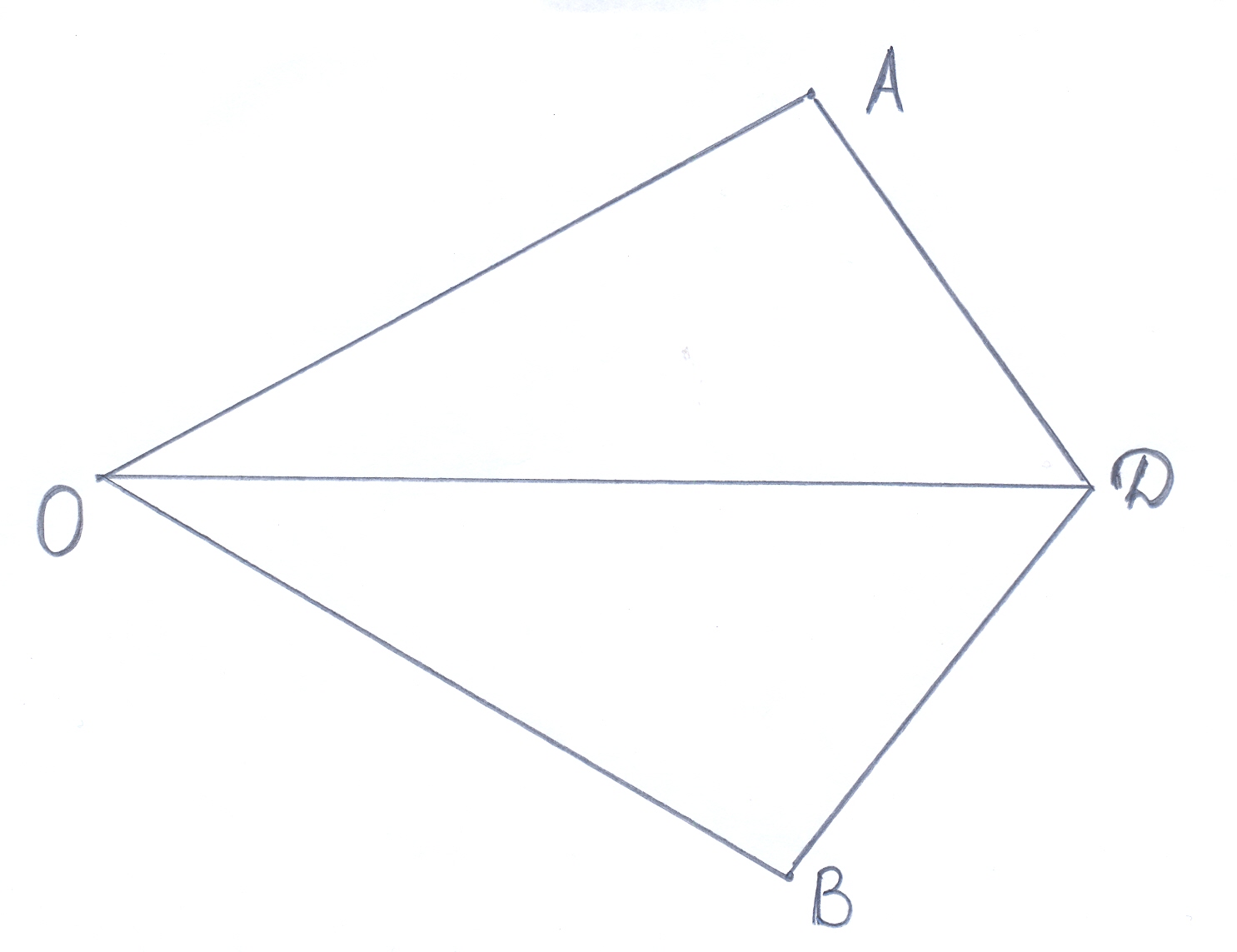
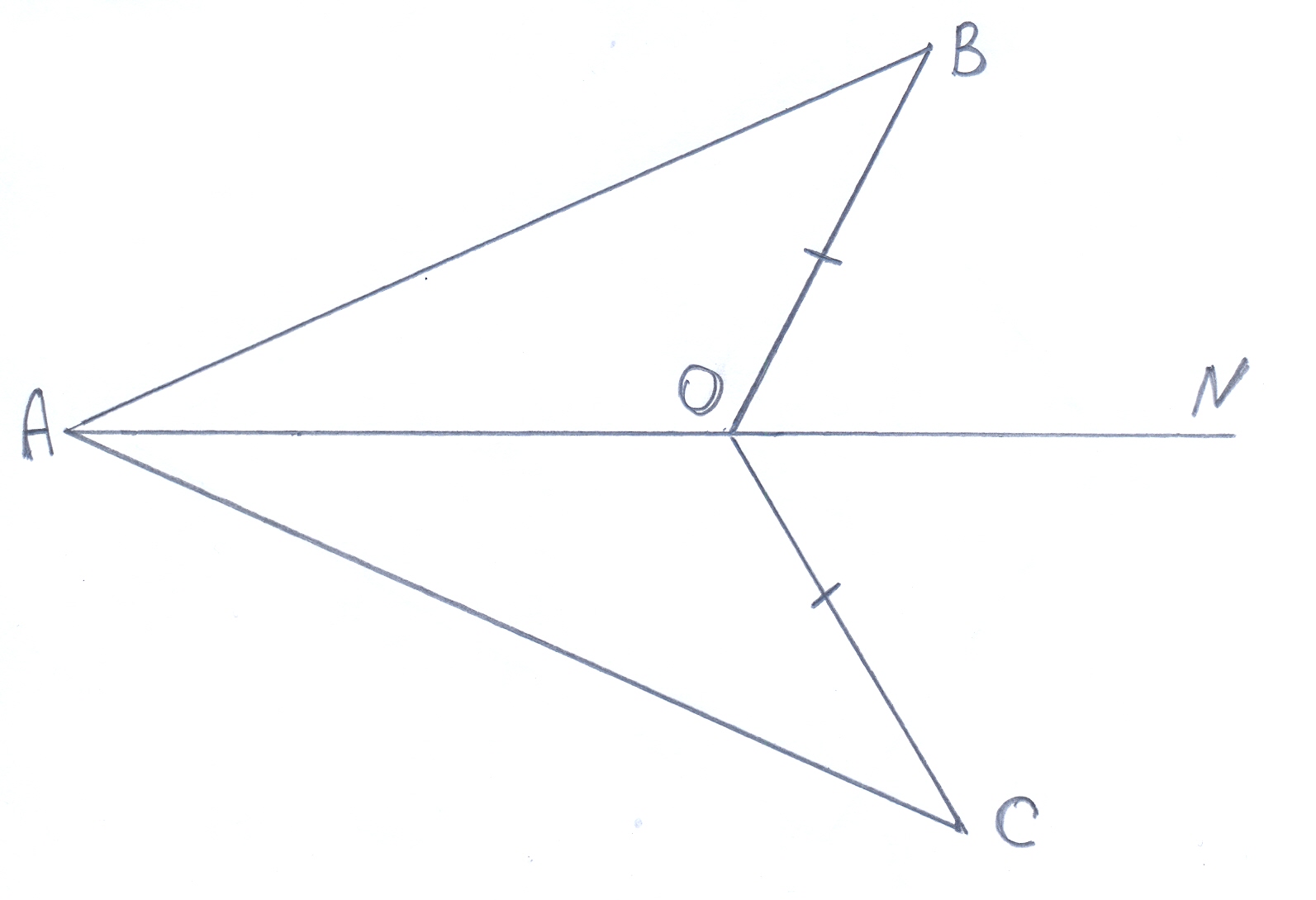
На рисунке АN – биссектриса < ВОС. Доказать: ∆ АОВ = ∆ АОС
Найдите < ДВА	Найдите < ДВА

3. Основная часть.

1) Решение задач на построение.

Учитель: Ну, а теперь за работу.

Задачи на построение, наверное, один из самых древних типов задач. При построении разрешается пользоваться лишь математической линейкой (односторонняя линейка без деления) и циркулем.

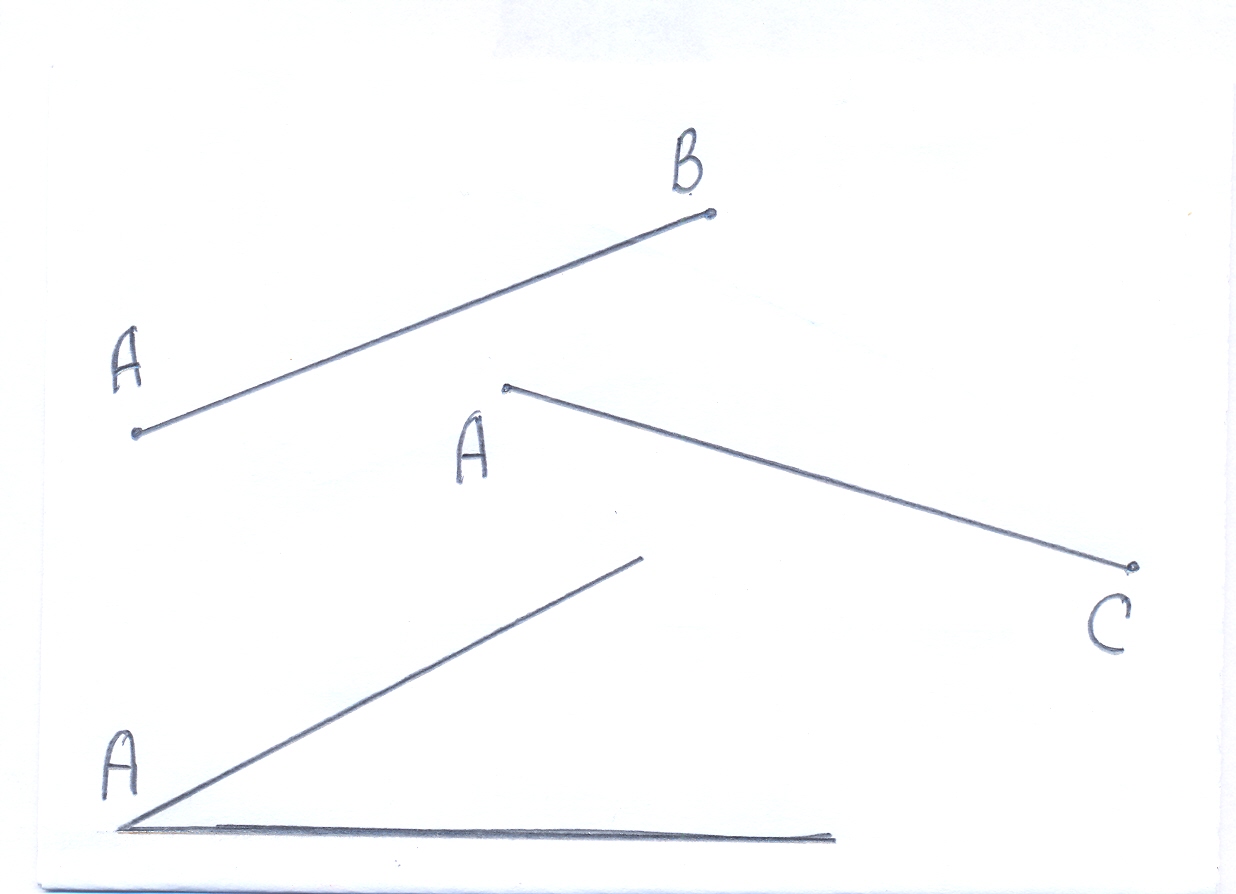
Вспомним задачи на построение треугольников по трем элементам. (К доске приглашаются три ученика.)

1) Построить треугольник АВС

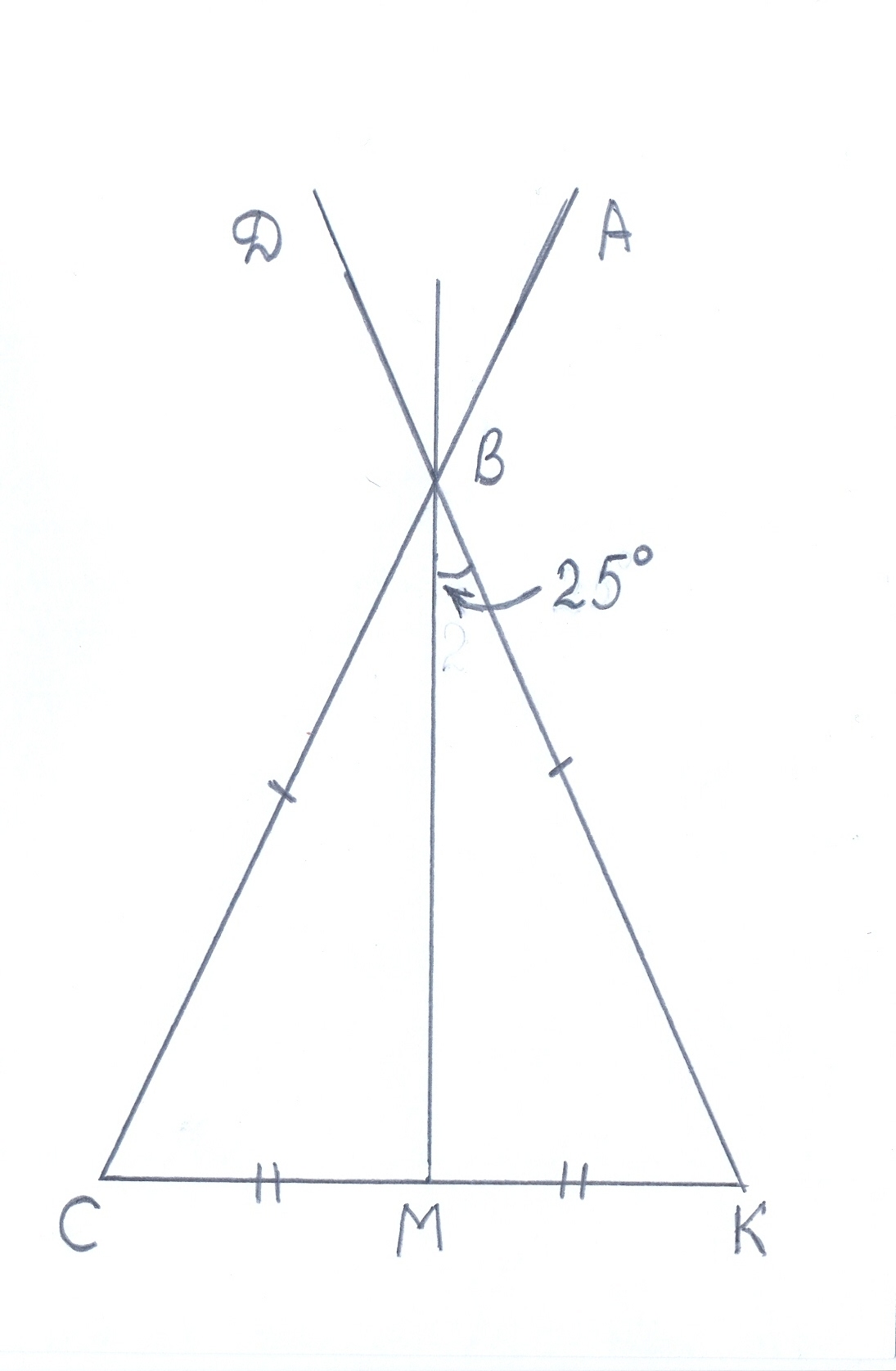
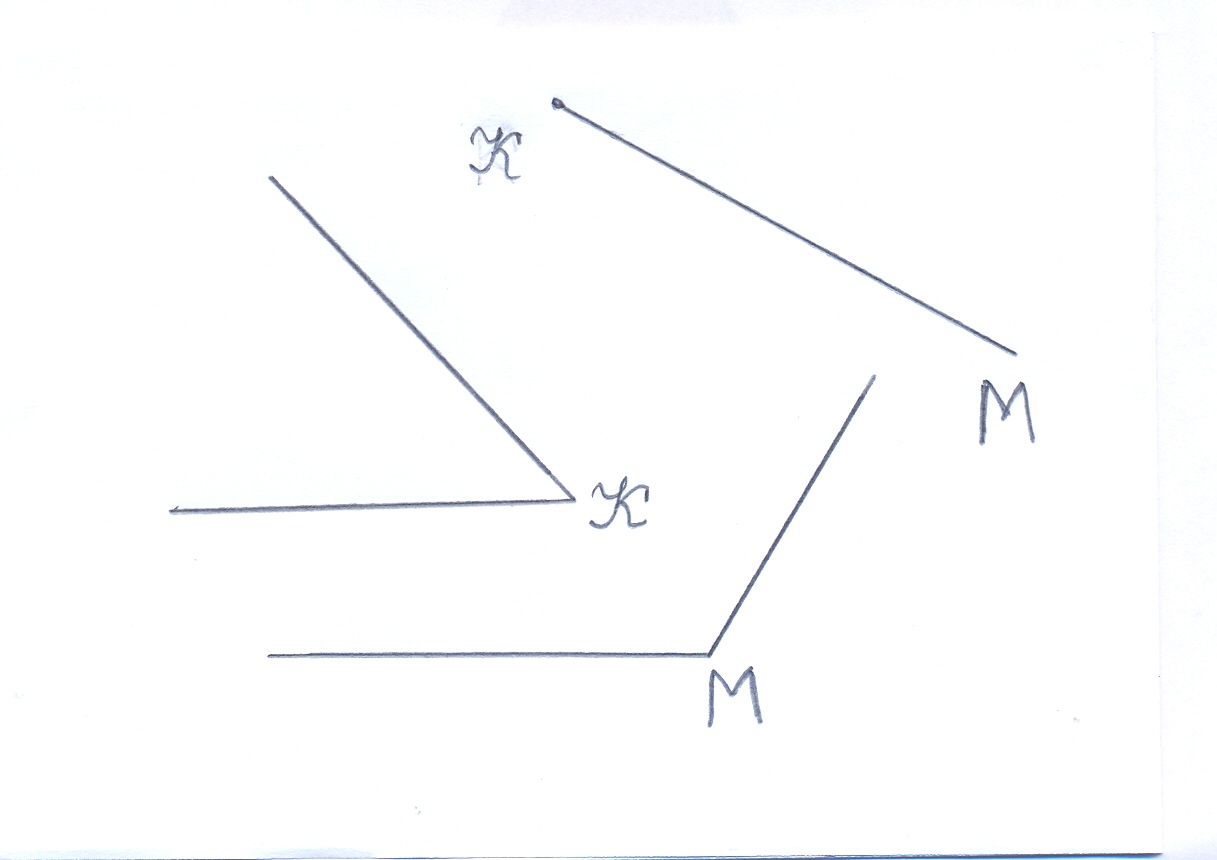
2) Построить треугольник KMN
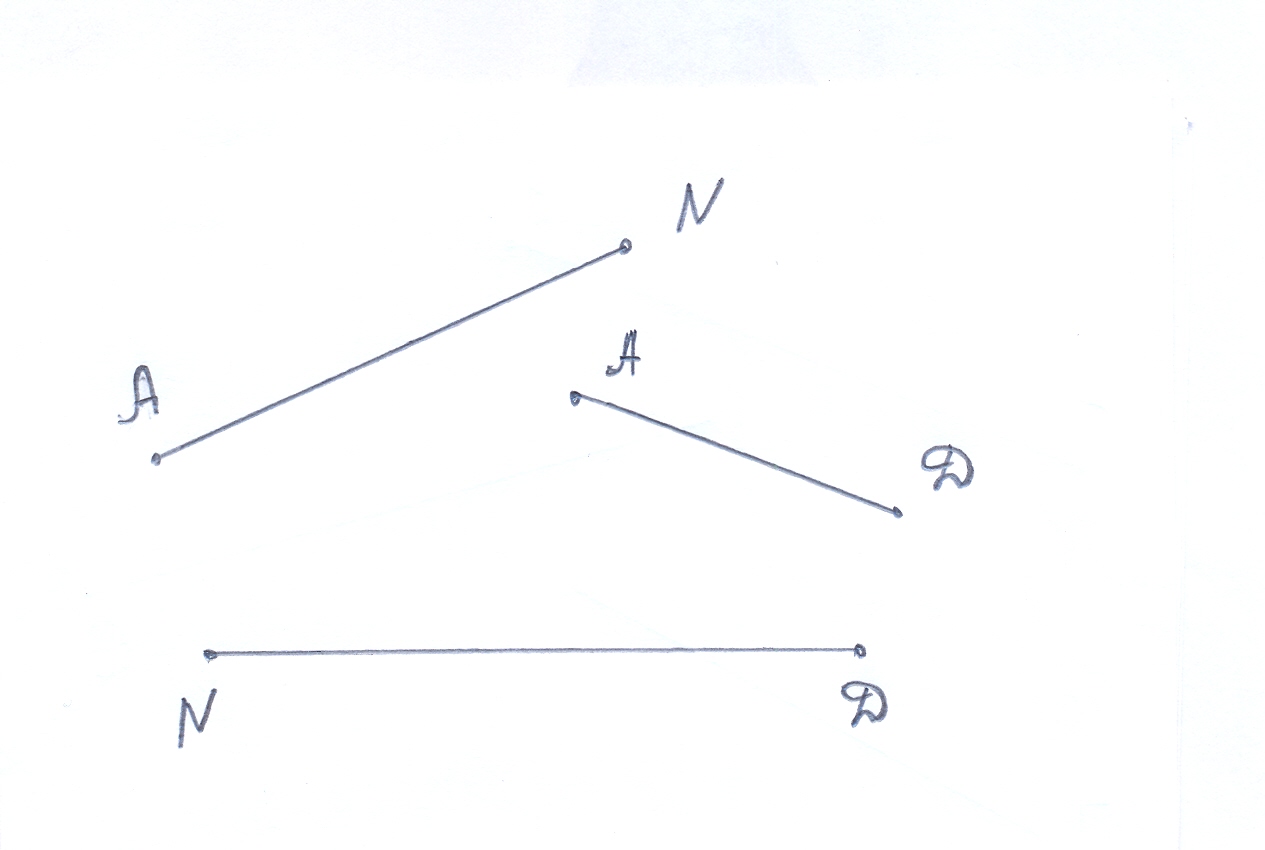
3) Построить треугольник АDN

Учитель: И вы, ребята, тоже приступайте к работе. У вас на столах лежат конверты с заданиями. Откройте свои конверты и выполняйте задания.

(Ребята выполняют индивидуально работу)

Учитель: Вот все с задачами справились. Скажите, как бы вы сформулировали задачи на построение 1, 2 и 3, которые мы решали.

(Задача 1 – построение треугольника по двум сторонам и углу между ними. Задача 2 – построение треугольника по стороне и двум прилежащим углам. Задача 3 – построение треугольника по трем сторонам.)

Учитель: Ребята, а где вы еще встречали такие названия.

(Такие названия у признаков равенства треугольников)

Учитель: Конечно же! Эти задачи являются основными задачами на построение треугольников. И признаки равенства треугольников, доказанные нами и применяемые теперь при доказательстве, также являются основными. Будут и другие признаки равенства треугольников, и другие задачи на построение треугольников, но еще раз напоминаю, основные. Запомните это.

А теперь помогите мне решить такую задачу. Вчера при подготовке к этому уроку, пользуясь набором «Конструктор», я выполнила два построения: прямоугольника и треугольника. Но, наверное, я плохо закрутила гаечки, и посмотрите, что у меня получилось.

Учитель: Что изменилось у прямоугольника

(У прямоугольника изменились углы)

Учитель: А треугольник, изменилось ли что-либо в нем?

(Нет, треугольник остался без изменения.)

Учитель: То есть можно сказать, что треугольник – не изменяющаяся фигура или жесткая фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов.

Это свойство – жесткость треугольника используется на практике:

1. чтобы закрепить столб в горизонтальном положении, ставят подпорку;

2. при установке кронштейна в горизонтальном положении;

3. телеграфные столбы с подпоркой, такие столбы называют анкерными;

4. стрела башенного крана закрепляется стальными канатами, образуя фору треугольника.

2) Решение задач на доказательство.

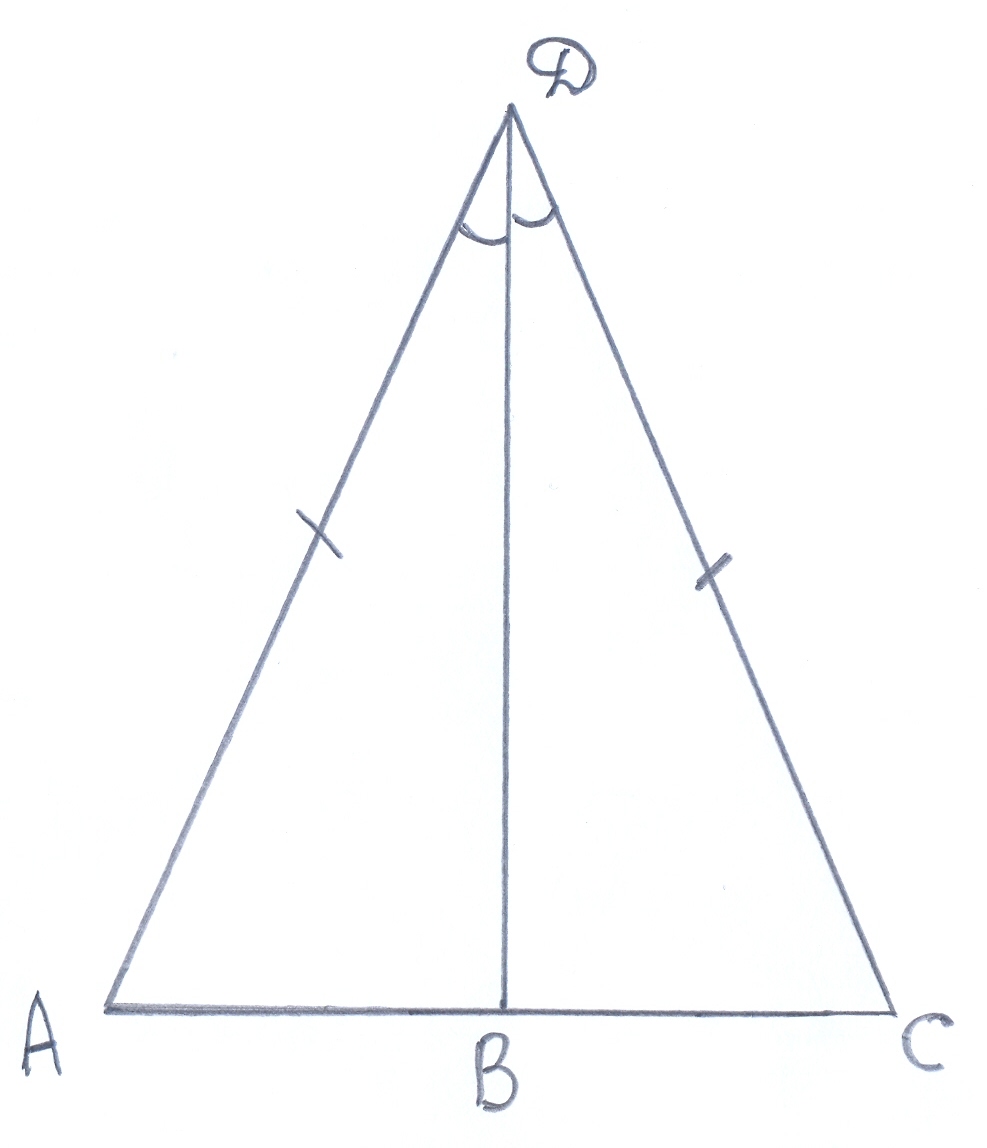
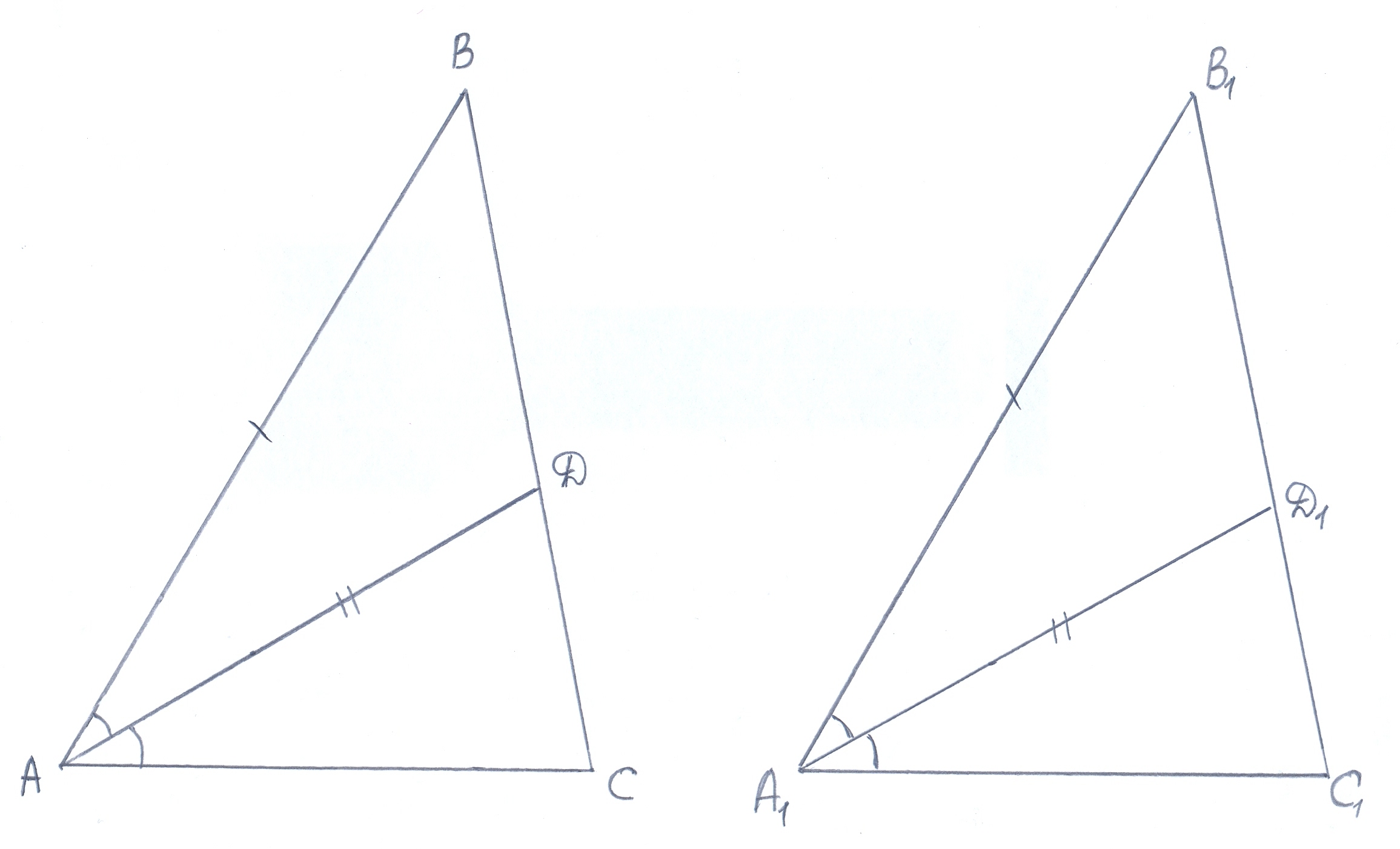
Учитель: Сейчас нас ждет следующая задача: «Докажите, что треугольники АВС и А₁В₁С₁ равны, если АВ = А₁В₁,<А = <А₁, АД = А₁Д₁, где АД = А₁Д₁ — биссектрисы треугольников АВС и А₁В₁С₁. Оформим решение этой задачи.

(Ученик выходит к доске и оформляет решение задачи)

Дано: ∆ АВС, ∆ А1В1С1 АВ = А1В1,<А = <А1, АД — биссектриса < А А1Д1 — биссектриса <А1, АД = А1Д1 Доказать: ∆ АВС =∆ А1В1С1

Доказательство:

рассмотрим ∆ АВД и ∆ А₁В₁Д₁:

1. АВ = А₁В₁ ( по условию)

2. АД = А₁Д₁ ( по условию)

3. <ВАД = < В₁А₁Д₁ (как половины равных углов <А и <А₁).

Тогда по двум сторонам и углу между ними , ∆ АВД = ∆ А₁В₁Д₁, отсюда следует, что ,<В = <В₁, как соответственные углы равных треугольников.

Рассмотрим ∆ АВС, ∆ А₁В₁С₁:

1. АВ = А₁В₁ ( по условию)

2. <А = <А₁ ( по условию)

3. <В = <В₁ ( по доказанному), тогда ∆ АВС= ∆ А₁В₁С₁ по двум сторонам и углу между ними. Итак, ∆ АВС = ∆ А₁В₁С₁.

3) Решение практических задач.

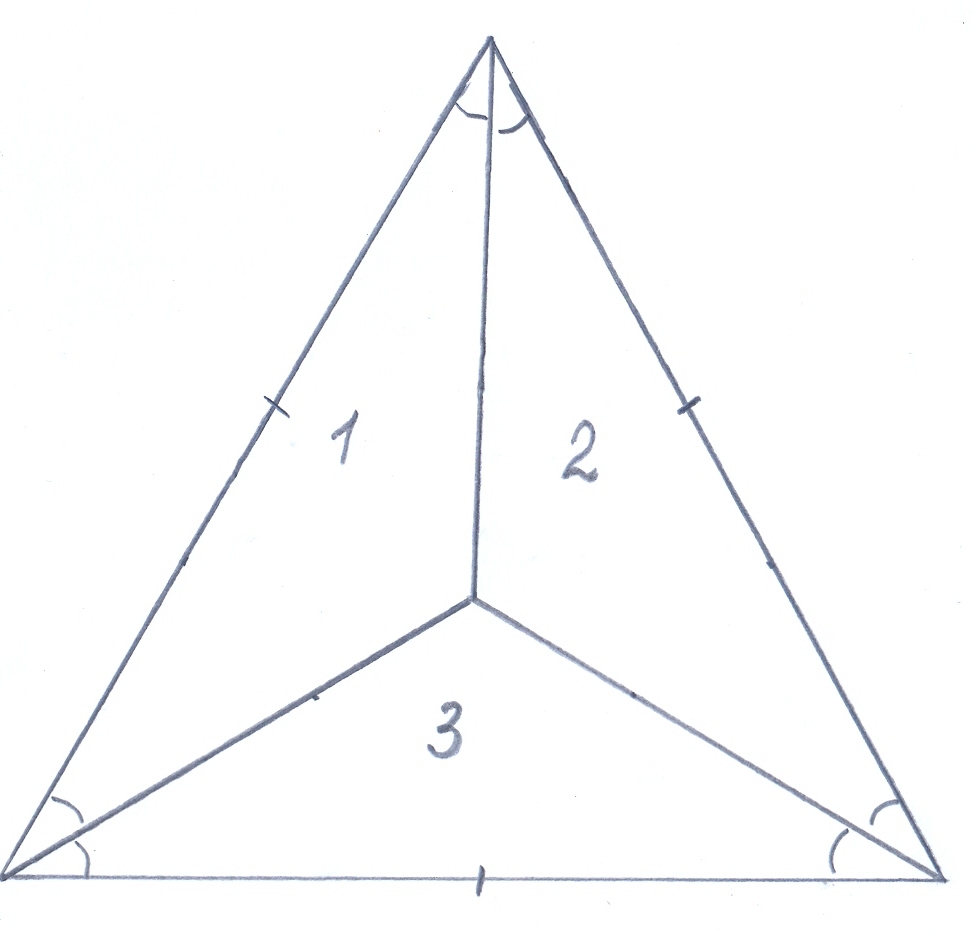
Учитель: Ну, а теперь, предлагаю вам отдохнуть. Однако отдых будет необычным. Представьте, что мы с вами находимся в осеннем лесу. Дорога до леса была длинная, мы с вами устали. Расположились на полянке, чтобы перекусить. А в дальнюю дорогу мы с вами взяли курники, они все треугольной формы, причем имеют форму правильного треугольника. Курники большие, и взяли то мы их всего 5 штук, нас же 15 человек. Как же нам эти пирожки разделить поровну. Сейчас вы должны эту задачу решить с помощью циркуля, линейки и ножниц. Итак, ждем правильного решения. Кто найдет правильное решение, должен объяснить нам его.

( Учащиеся работают парами)

Строим биссектрисы углов треугольника. ∆1 = ∆2 = ∆3 по стороне и двум прилежащим углам.

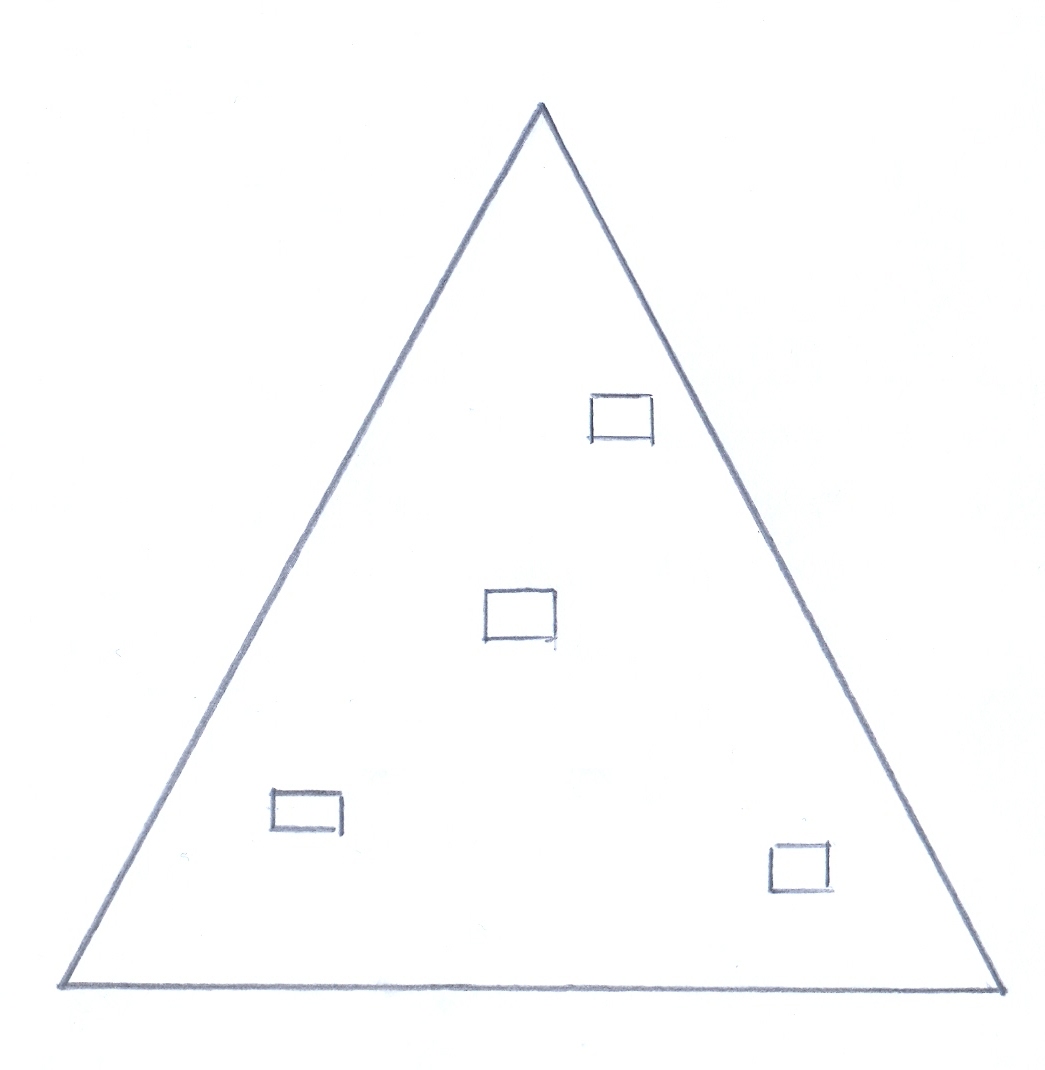
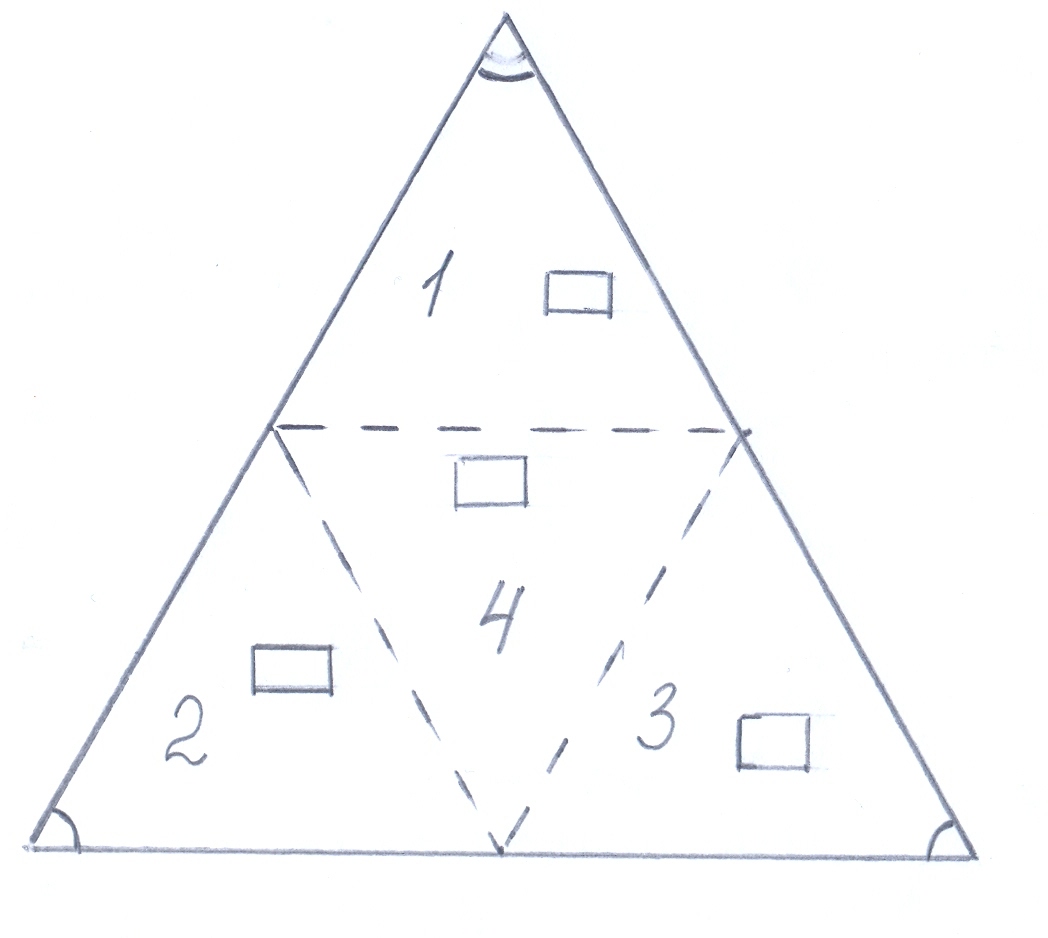
Учитель: Перекусить-то мы с вами перекусили, да день оказался жарким. Хочется и водички испить. Здесь рядом находится колодцы. Но нам разрешат напиться только в том случае, если мы поможем хозяевам этих колодцев разрешить такую задачу: «Четверо соседей получили вместе участок земли треугольной формы (форма правильного треугольника). На этом участке имеется 4 колодца. Как разделить этот участок на 4 участка одинаковые по форме, равные по площади и чтобы на каждом из них было по одному колодцу. Ну, что ж, за дело. Можете воспользоваться циркулем, линейкой. Но не разрезайте.

( Учащиеся работают парами)

Находим середины сторон. ∆1 = ∆2 = ∆3 по двум сторонам и углу между ними. ∆4=∆1 = ∆2 = ∆3 по трем сторонам.

4. Заключительная часть урока

Учитель: Ну, что, ребята. Урок подходит к концу и в завершении урока я предлагаю вам отгадать кроссворд:

				1
2
					3
					4
		5
					6
				7
		8

1 – отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника; (медиана)

2 – геометрическая фигура; (треугольник)

3 – великий русский геометр; (Лобачевский)

4 – часть прямой; (отрезок)

5 – единица измерения углов; (градус)

6 – прибор для построения окружности; (циркуль)

7 – перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону; (высота)

8 — что говорят учащиеся на слова завуча: «Урока математики не будет. Учитель заболел».(ура!)

(После отгадывания слова под цифрой 3 учащиеся рассказывают о Н.И.Лобаческом)

Великий русский геометр Николай Иванович Лобачевский (1792 – 1856). У здания Казанского университета стоит памятник, построенный в 1896 году в честь великого ученого. Стихотворение Фирсова описывает личность Лобачевского, запечатленного в фигуре этого памятника.

Н.И.Лобачевскому.

Высокий лоб, нахмуренные брови

В холодной бронзе – отраженный луч…

Но даже неподвижный и суровый

Он, как живой, — спокоен и могуч.

Когда – то здесь, на площади широкой,

На этой вот Казанской мостовой,

Задумчивый, неторопливый, строгий

Он шел на лекции – великий и живой

Пусть новых линий не начертят руки,

Он здесь стоит, взнесенный высоко,

Как утверждение бессмертья своего,

Как вечный символ торжества науки.

Вся жизнь Н.И.Лобачевского была связана с Казанским университетом: студент, магистр, профессор, декан, ректор.

В течение 19 лет он – ректор Казанского университета.

Следующие два примера из его жизни свидетельствуют об энергии и активности Лобачевского на благо университета.

Когда в 1830 году, свирепствовавшая в Поволжье холера, достигла Казани, Лобачевский сразу же принял в отношении университета героические меры. Изолировал университет от всего остального города, организовал проживание и питание студентов на университетской территории . Благодаря этим мерам эпидемия не затронула университет.

В 1842 году Казань подверглась другому бедствию – страшному по своим опустошительным последствиям пожару. Во время этого пожара Лобачевский проявил нужное хладнокровие и распорядительность, которые помогли спасти от огня университетское имущество и астрономические инструменты.

Н.И.Лобачевский не только выдающийся ученый, прекрасный педагог, но и уважаемый студентами человек, пример для подражания во многом.

5. Подведение итогов урока.

Учитель: Вот и закончилось наше путешествие, в котором вы показали неплохие знания по теме «Треугольники. Признаки равенства треугольников». В ходе урока мы повторили основные понятия, признаки, свойства, связанные с треугольником. Однако треугольник еще долго будет нам с вами встречать в ходе изучения геометрии. Еще очень много мы узнаем об этом простом, но «загадочном» треугольнике. За работу же на уроке я вам говорю: «Молодцы!».

( Выставление оценок за урок)

Домашним задание будет: подготовить кроссворд из 8-10 слов на тему «Треугольник»

Спасибо вам за урок. До свидания.

Используемая литература:

1. Атанасян Л.С. и др. « Геометрия, 7-9» (учебник для общеобразовательных

учреждений)- М. Просвещение, 2007

2. Гусев В.А, Медяник А.И. «Дидактические материалы по геометрии», М.

Просвещение, 1991

3. Козина М.Е., Фадеева О.М. «Математика. 5-11 классы: нетрадиционные формы

организации тематического контроля на уроках», Волгоград, Учитель, 2006

4. Коваленко В.Г. «Дидактические игры на уроках математики», М.Просвещение,

1990

5. Медяник А.И. «Учителю о школьном курсе геометрии» М., Просвещение, 1984

6. Рогулева А.В. 7 класс. Рабочая тетрадь Саратов, Лицей, 2007

7. Саврасова СМ., Ястребинецкий Г.А. «Упражнения по планиметрии на готовых

чертежах» М., Просвещение, 1987

8. Фальке Л.Я. «Час занимательной математики», М., Илекса, 2005

9. Шарыгин И.Ф., Ерганжиева Л.Н. «Наглядная геометрия», М. МАРТА, 1992

Интернет- ресурсы:

http://forum.club-films.tv

http ://img .new -warez .net .ru /_ph /1/728153575.jpg