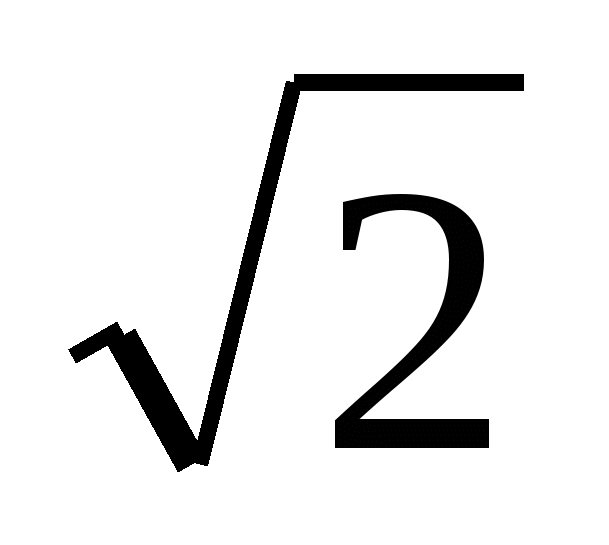ДИАГНОСТИЧЕСКАЯ РАБОТА ПО ГЕОМЕТРИИ

Хакимова Альфия Узбековна,

МОБУ СОШ № 1, учитель математики, Башкортостан, г.Мелеуз.

Предмет (направленность): математика.

Возраст детей: 9 классы.

Место проведения: класс.

Диагностическая работа по геометрии

для обучающихся 9 классов (апрель 2013)

Вариант 1

1. Два угла треугольника равны 40˚ и 130˚. Найдите величину внешнего угла при третьей вершине. Ответ дайте в градусах.

2. Один из углов параллелограмма в 3 раза больше другого. Найдите меньший из углов параллелограмма. Ответ дайте в градусах.

3. Диагонали ромба равны 24 и 7,5. Найдите его площадь.

4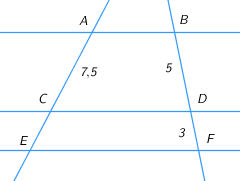. Прямые AB, CD и EF параллельны. По данным рисунка найдите длину отрезка CE.

5. Какие из следующих утверждений верны?

1. Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2. Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.

3. Диагонали ромба пересекаются под прямым углом.

4. Диагонали прямоугольника пересекаются под прямым углом.

6. Найдите угол А треугольника АВС, если его медиана ВМ равна половине стороны АС, а угол ВТС, образованный биссектрисой ВТ и стороной АС, равен 65⁰ .

7. В круге проведены диаметр АВ и хорда СТ. Докажите, что если СА = ТА, то и СВ = ТВ .

Вариант 2

1. Один из углов равнобедренного треугольника равен 100˚. Найдите любой другой его угол. Ответ дайте в градусах.

2. В трапеции ABCD AB=BC=CD . Точки K,L,M и N — середины сторон трапеции. Найдите наибольший угол четырёхугольника KLMN , если угол BAD равен 40˚ . Ответ дайте в градусах.

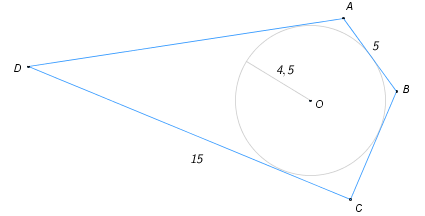
3. Найдите площадь описанного около окружности радиуса 4,5 четырёхугольника ABCD, если AB=5 и CD=15.

4. Катеты прямоугольного треугольника равны 9 и 12. Найдите длину высоты, проведенной к гипотенузе треугольника.

5. Укажите номера верных утверждений.

1. Через любую точку прямой на плоскости можно провести единственный перпендикуляр к этой прямой.

2. Существует треугольник с двумя равными тупыми углами.

3. Параллелограмм с равными диагоналями – это прямоугольник.

6. KA и KB — хорды окружности с центром в точке O, ∠AKB = 30⁰ . Найдите радиус окружности, если длина хорды AB равна 6.

7. Медианы AM и BN в треугольнике ABС пересекаются в точке O. Докажите, что треугольники AOB и MON подобны.

Вариант 3

1. В прямоугольном треугольнике один из углов равен 40˚. Найдите внешний угол при вершине второго острого угла. Ответ дайте в градусах.

2. Правильный шестиугольник вписан в окружность. С – произвольная точка окружности. Найдите угол ACB в градусах.

3. Основания равнобедренной трапеции равны 23 и 17. Тангенс одного из углов равен 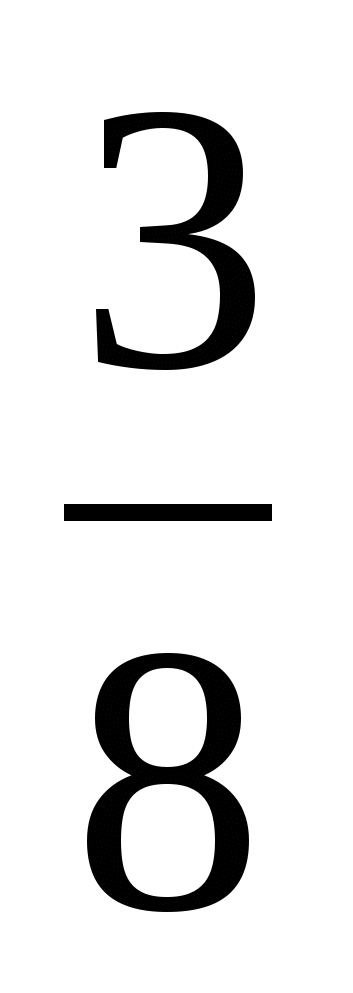. Найдите площадь трапеции.

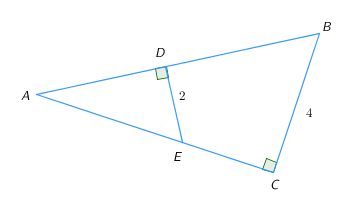
4. В треугольнике ABC проведены высоты BD и CE . Известны длины отрезков AC=8 , AB=12 , AD=6 . Найдите AE .

5. Какие из следующих утверждений верны?

1. В любой четырёхугольник можно вписать окружность.

2. Центром окружности, вписанной в правильный треугольник, является точка пересечения серединных перпендикуляров к его сторонам.

3. В треугольнике против меньшего угла лежит меньшая сторона.

4. Внешний угол треугольника равен сумме внутренних, не смежных с ним.

6. Прямые AB и CD параллельны. Между прямыми отмечена точка К так, что 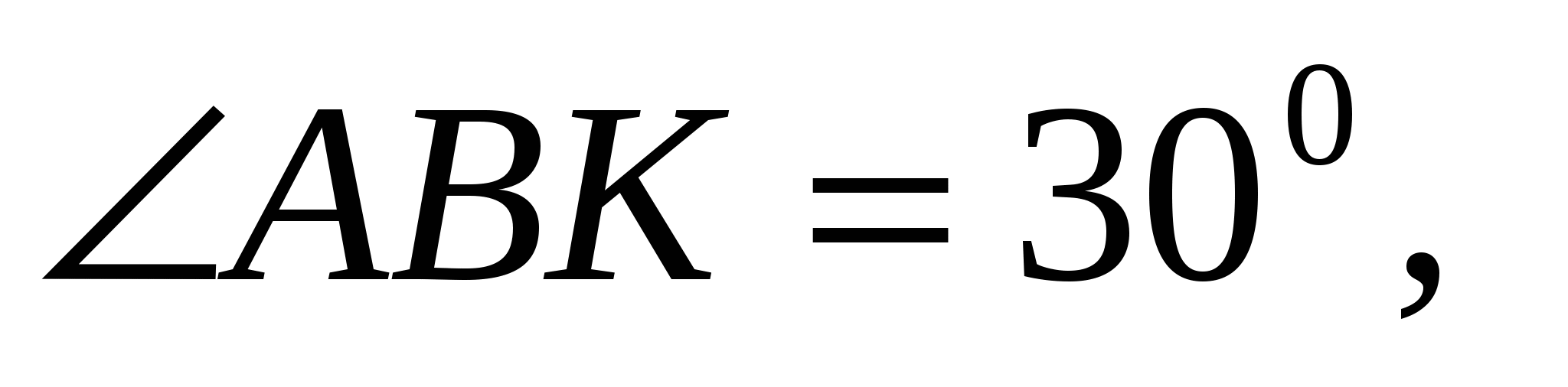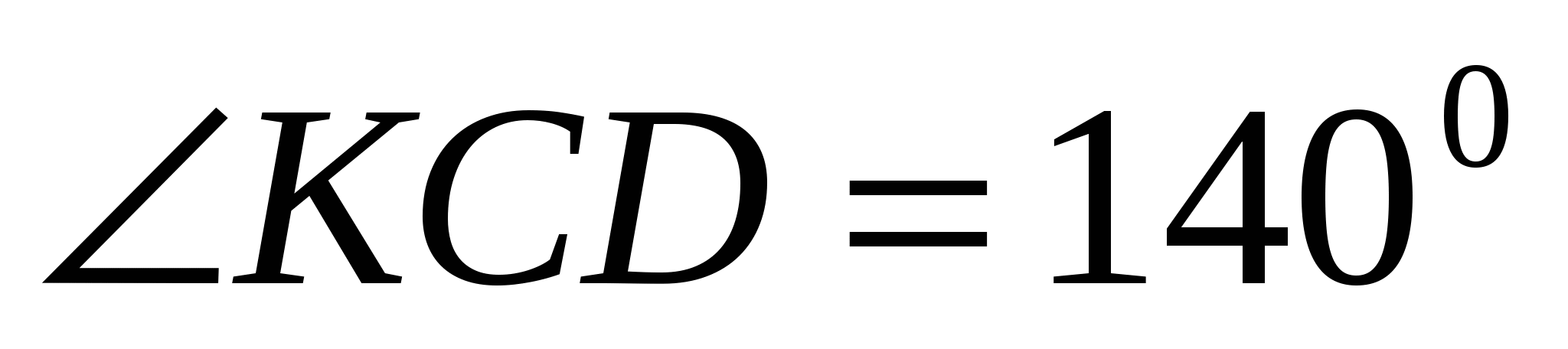. Найдите величину угла BКC.

7. В круге проведены диаметр АВ и равные хорды АС и ВТ, причём точки С и Т лежат по разные стороны от АВ. Докажите, что АС и ВТ параллельны.

Вариант 4

1. В прямоугольном треугольнике внешний угол при вершине острого угла равен 110˚. Найдите другой острый угол треугольника. Ответ дайте в градусах.

2. Треугольник АВС вписан в окружность. Известны два его угла ∠A=80˚,∠B=55˚. Найдите градусную меру меньшей дуги AB.

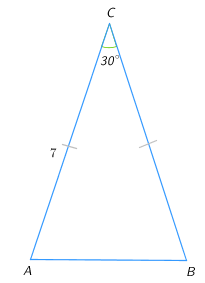
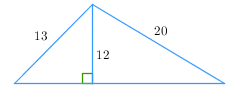
3. Найдите площадь равнобедренного треугольника, изображенного на рисунке.

4. Площадь параллелограмма равна 8, а высоты параллелограмма равны 2 и 1,6. Найдите периметр параллелограмма.

5. Укажите номера верных утверждений.

1. В равностороннем треугольнике все углы равны.

2. Четырехугольник с прямыми углами — это квадрат.

3. В равнобедренной трапеции диагонали равны.

6. Угол А треугольника АВС равен 54⁰ . Найдите больший из углов между биссектрисами углов В и С.

7. Медианы BM и CK в треугольнике ABC пересекаются в точке O, Докажите, что треугольники СOB и KOM подобны.

Вариант 5

1. Один из внешних углов равнобедренного треугольника равен 40˚. Найдите угол при основании этого треугольника. Ответ дайте в градусах.

2. На рисунке точка O – центр окружности, а треугольник OAB – равносторонний. Найдите величину угла ACB в градусах.

3. Диагональ AC ромба ABCD равна 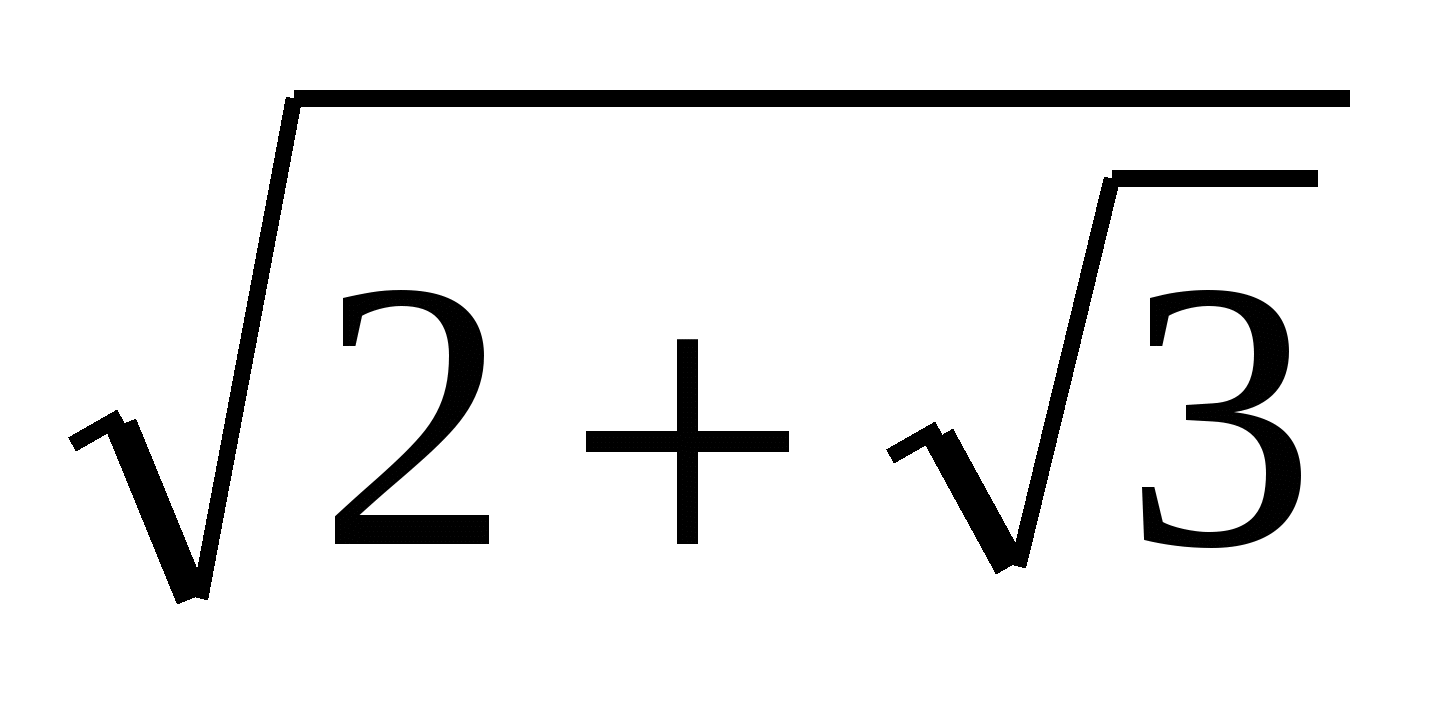, а угол при вершине C равен 30˚. Найдите площадь треугольника ACD.

4. В прямоугольном треугольнике ABC из произвольной точки E катета AC опущен перпендикуляр ED на гипотенузу AB . DE=2 , BC=4 . Площадь треугольника ADE равна 5 . Найдите площадь треугольника ABC .

5. Какие из следующих утверждений верны?

1. Если диагонали четырёхугольника делят его углы пополам, то этот четырёхугольник — ромб.

2. Центром окружности, описанной около правильного треугольника, является точка пересечения его высот.

3. Треугольник, стороны которого равны 7, 12, 13 является прямоугольным.

4. Любые два прямоугольных треугольника подобны.

6. Найдите угол С треугольника АВС, если его медиана ВМ равна половине стороны АС, а угол ВТА, образованный биссектрисой ВТ и стороной АС, равен 80⁰ .

7. ABCD — параллелограмм. На сторонах AB, BC, CD, DA отмечены соответственно точки P, K, M и N так, что BK =ND , BP =MD. Докажите, что четырехугольник PKM N – параллелограмм.

Вариант 6

1. В равнобедренном треугольнике ABC с основанием AC угол B равен 42˚. Найдите величину угла CAK, если AK — биссектриса угла A. Ответ дайте в градусах.

2. Два угла вписанного в окружность четырехугольника равны 72˚ и 118˚. Найдите меньший из оставшихся углов. Ответ дайте в градусах.

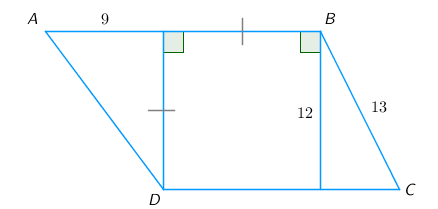
3. Найдите периметр трапеции ABCD по данным рисунка.

4. Площадь прямоугольного треугольника с катетами 4 и 3 равна площади ромба со стороной 5. Найдите высоту ромба.

5. Укажите номера верных утверждений.

1. Медиана треугольника делит треугольник на два равных.

2. Зная только длины двух сторон треугольника, можно найти его площадь.

3. Если в треугольнике равны два угла, то он равнобедренный.

6. Прямые AB и CD параллельны. Между прямыми отмечена точка М так, что 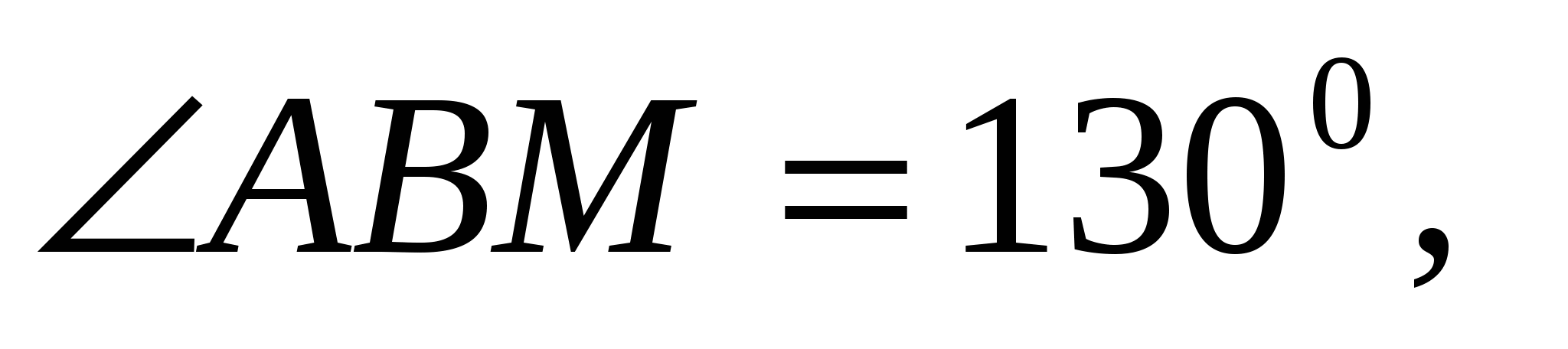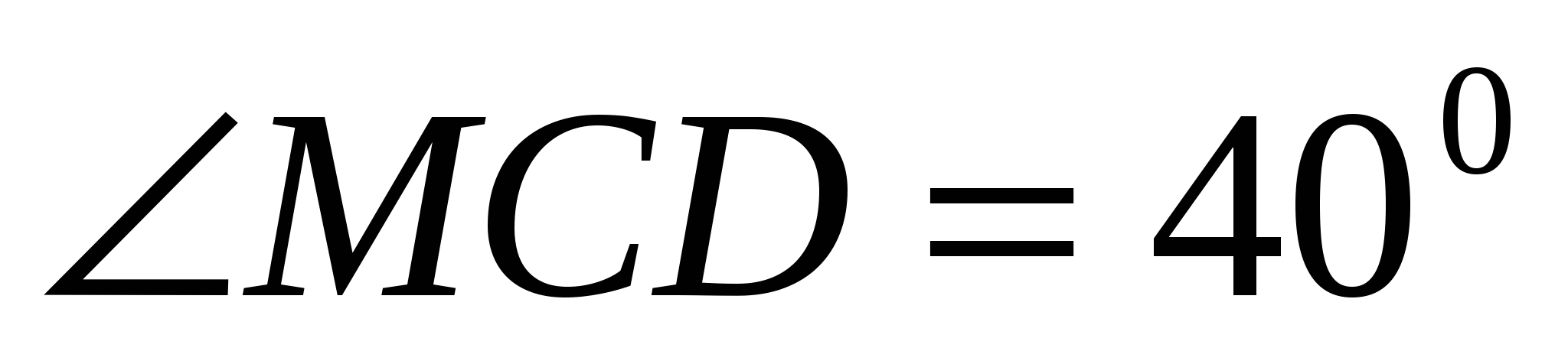. Найдите величину угла BMC.

7. В круге проведены диаметр АВ и параллельные хорды АС и ВТ. Докажите, что СВ = ТА .

Вариант 7

1. Параллельные прямые AB и CD пересечены секущей AC. CB – биссектриса угла C , ∠CAB=50˚ . Найдите угол ACB .

2. На рисунке точка O − центр окружности, а треугольник OAB − прямоугольный. Найдите величину угла ACB в градусах.

3. Найдите площадь треугольника, изображенного на рисунке. Сторону клетки считать равной 1 см.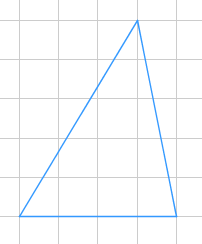

4. Высота равнобедренного треугольника, проведенная к его основанию, равна 4. Длина основания равна 6. Найдите длину высоты, проведенной к боковой стороне треугольника.

5. Укажите номера верных утверждений.

1. Биссектриса угла треугольника делит сторону треугольника пополам.

2. Диагонали равнобедренной трапеции равны.

3. Центр окружности, вписанной в равнобедренный треугольник, находится в точке пересечения его высот.

6. Угол А треугольника АВС равен 64⁰. Найдите меньший из углов между биссектрисами углов В и С.

7. ABCD — параллелограмм. На сторонах AB, BC, CD, DA отмечены соответственно точки P, K, M и N так, что KC = AN , BP = MD. Докажите, что четырехугольник PKMN – параллелограмм.

Вариант 8

1. В треугольнике ABC, углы которого равны ∠B=40˚ и ∠C=80˚,проведена высота CH. Найдите величину угла ACH (в градусах).

2. Прямая KA касается окружности с центром O в точке А. Радиус окружности равен 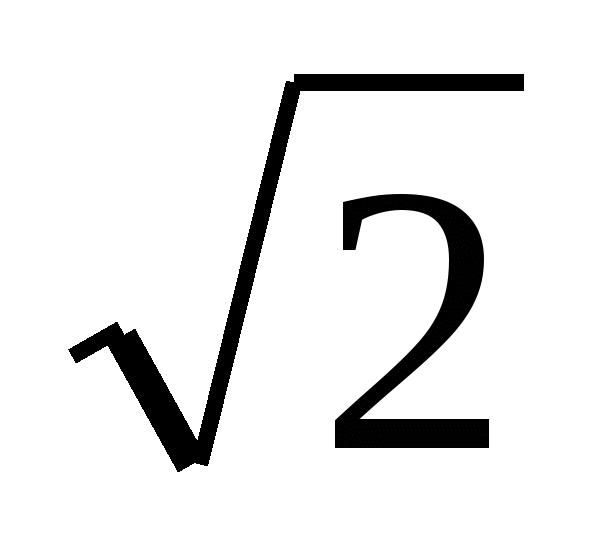. Расстояние от точки K до центра окружности равно 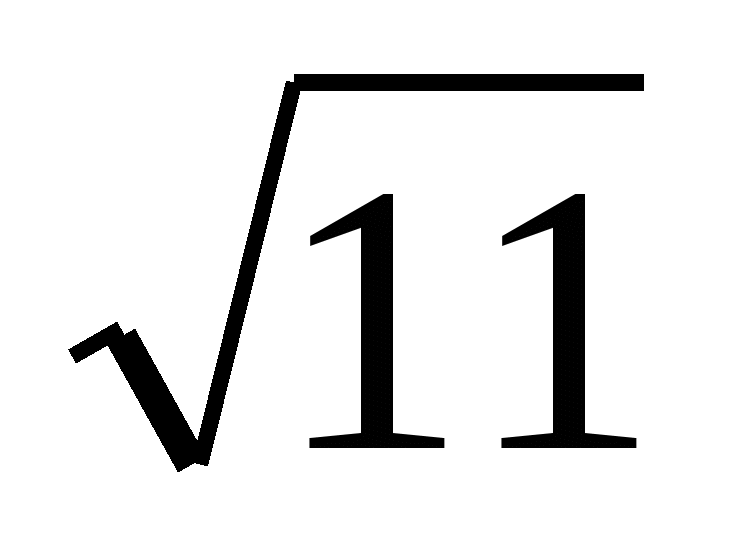. Найдите AK.

3. . Найдите площадь треугольника, изображенного на рисунке.

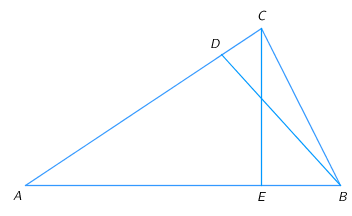
4. В треугольнике АВС отрезок DE параллелен отрезку AB . DC=12, DA=3, DE=4. Найдите AB.

5. Какие из следующих утверждений верны?

1. В любой прямоугольный треугольник можно вписать окружность.

2. Каждая сторона треугольника больше суммы двух других сторон.

3. Существует треугольник ABC с меньшей стороной AC и углами ∠A=43, ∠C=72 .

4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.

5. Любые два равнобедренных треугольника подобны.

6. KA и KB — хорды окружности с центром в точке O, ∠AKB = 45°. Найдите длину хорды AB, если радиус окружности равен 4.

7. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

Решения заданий № 6, №7

(Замечание. Учащийся вправе привести любое другое верное и полное решение, доказательство.)

Вариант 1

№6. Найдите угол А треугольника АВС, если его медиана ВМ равна половине стороны АС, а угол ВТС, образованный биссектрисой ВТ и стороной АС, равен 65⁰.

Ответ: 20⁰ .

Решение: так как медиана ВМ треугольника АВС равна половине стороны АС, то АВС – прямоугольный треугольник и его угол В равен 90⁰ . Так как угол АВТ , равный половине угла АВС, равен 450 , то угол А , равный разности углов ВТС и АВТ, составит 65⁰ – 45⁰ = 20⁰ .

№7. В круге проведены диаметр АВ и хорда СТ. Докажите, что если СА = ТА, то и СВ = ТВ .

Доказательство: так как АВ – диаметр, то углы АСВ и АТВ – прямые. Треугольники АСВ и АТВ равны по катету и гипотенузе. Поэтому и СВ = ТВ .

Вариант 2

№6. KA и KB — хорды окружности с центром в точке O, ∠AKB = 30⁰ . Найдите радиус окружности, если длина хорды AB равна 6.

Решение:

1.∠AOB = 2∠AKB = 60°по свойству вписанного угла.

2.Треугольник AOB — равносторонний, значит, AO = AB = 6.

Ответ: AO = 6.

№7. Медианы AM и BN в треугольнике ABС пересекаются в точке O. Докажите, что треугольники AOB и MON подобны.

Доказательство:

1. Прямые MN и AB параллельны по свойству средней линии треугольника.

2.∠AMN = ∠BAM как накрест лежащие углы.

3. ∠BOA = ∠MON как вертикальные углы.

Треугольники AOB и MON подобны по двум углам.

Что и требовалось доказать.

Вариант 3

№6. Прямые AB и CD параллельны. Между прямыми отмечена точка К так, что 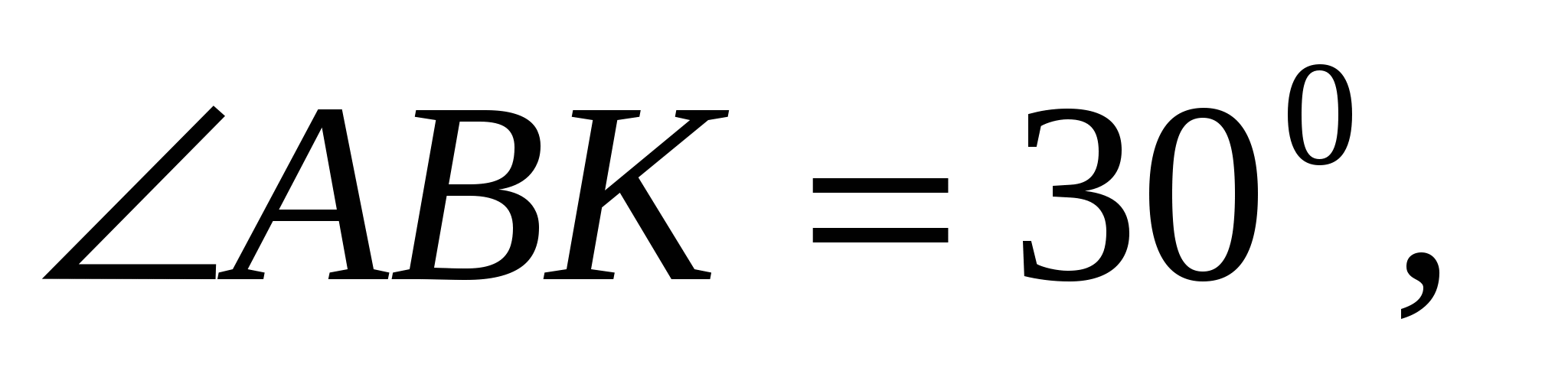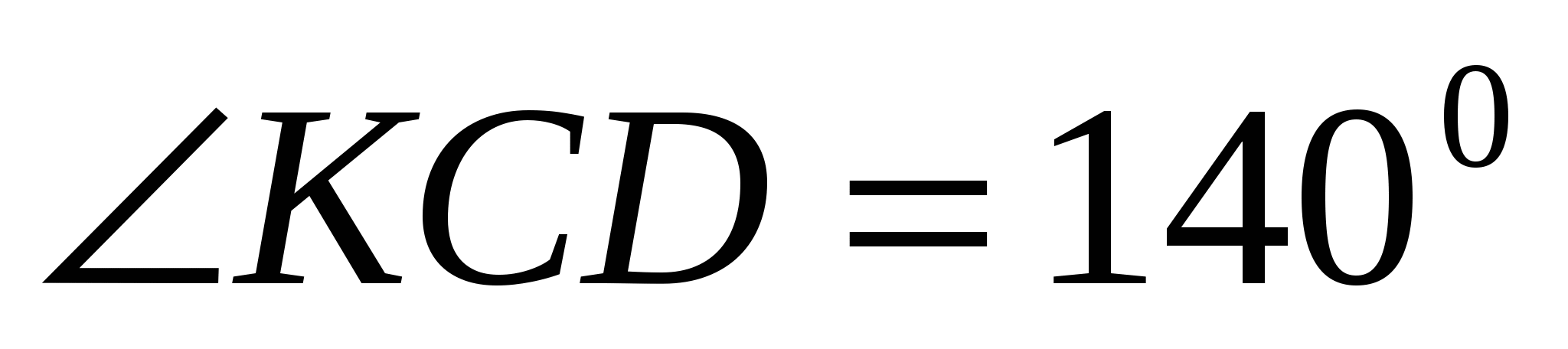. Найдите величину угла BКC.

Решение:

Через точку К проведем прямую КЕ, параллельную прямой АВ. Угол ВКЕ равен углу АВК равному 30°, как накрест лежащие углы при параллельных прямых АВ и КЕ, и секущей КВ. Углы KCD и KCF смежные, значит, угол KCF равен 40°. Углы ЕKC и KCF равны как накрест лежащие углы при параллельных прямых КЕ и CD, и секущей КС.

Значит, угол ВКС равен 70°.

Ответ: 70°.

№7. В круге проведены диаметр АВ и равные хорды АС и ВТ, причём точки С и Т лежат по разные стороны от АВ. Докажите, что АС и ВТ параллельны.

Доказательство: так как АВ – диаметр, то углы АСВ и ВТА – прямые. Треугольники АСВ и ВТА равны по гипотенузе и катету. Поэтому равны и внутренние накрест лежащие углы САВ и АВТ , так что АС и ВТ параллельны.

Вариант 4

№6. Угол А треугольника АВС равен 54⁰ . Найдите больший из углов между биссектрисами углов В и С.

Ответ: 117⁰ .

Решение: обозначим за ВК и СМ биссектрисы треугольника АВС, а за О – точку пересечения биссектрис. Тогда угол МОВ будет равен сумме углов ОВС и ОСВ, то есть полусумме углов В и С треугольника АВС. Искомый угол СОВ равен 1800 минус угол МОВ , поэтому он равен 180⁰ – (180⁰ – 54⁰)/2 = 117⁰.

№7. Медианы BM и CK в треугольнике ABC пересекаются в точке O, Докажите, что треугольники СOB и KOM подобны.

Доказательство:

1. Прямые MK и BC параллельны по свойству средней линии треугольника.

2.∠BMK = ∠CBM (как накрест лежащие углы).

3. ∠BOC = ∠MOK (как вертикальные углы).

Треугольники COB и KOM подобны по двум углам.

Что и требовалось доказать.

Вариант 5

№6. Найдите угол С треугольника АВС, если его медиана ВМ равна половине стороны АС, а угол ВТА, образованный биссектрисой ВТ и стороной АС, равен 80⁰ .

Ответ: 35⁰ .

Решение: так как медиана ВМ треугольника АВС равна половине стороны АС, то АВС – прямоугольный треугольник и его угол В равен 90⁰ . Так как угол СВТ , равный половине угла АВС, равен 450 , то угол С , равный разности углов ВТА и СВТ, составит 80⁰ – 45⁰ = 35⁰ .

№7. ABCD — параллелограмм. На сторонах AB, BC, CD, DA отмечены соответственно точки P, K, M и N так, что BK =ND , BP =MD. Докажите, что четырехугольник PKM N – параллелограмм.

Доказательство.

Треугольники ВРК и DMN равны по двум сторонам и углу между ними, т.к. ВК = DN, ВР = DM,

∠B =∠D (по свойству параллелограмма). Значит, стороны РК и MN равны.

ВК = DN, значит, AN = KC. ВР = DM, значит, AP = СM.

∠A =∠C (по свойству параллелограмма), значит, треугольники APN и KCM равны по двум сторонам и углу между ними. Значит, сторона PN равна стороне КМ. Таким образом, в четырехугольнике PKMN противоположные стороны равны.

Такой четырехугольник, по признаку параллелограмма – параллелограмм.

Вариант 6

№6. Прямые AB и CD параллельны. Между прямыми отмечена точка М так, что 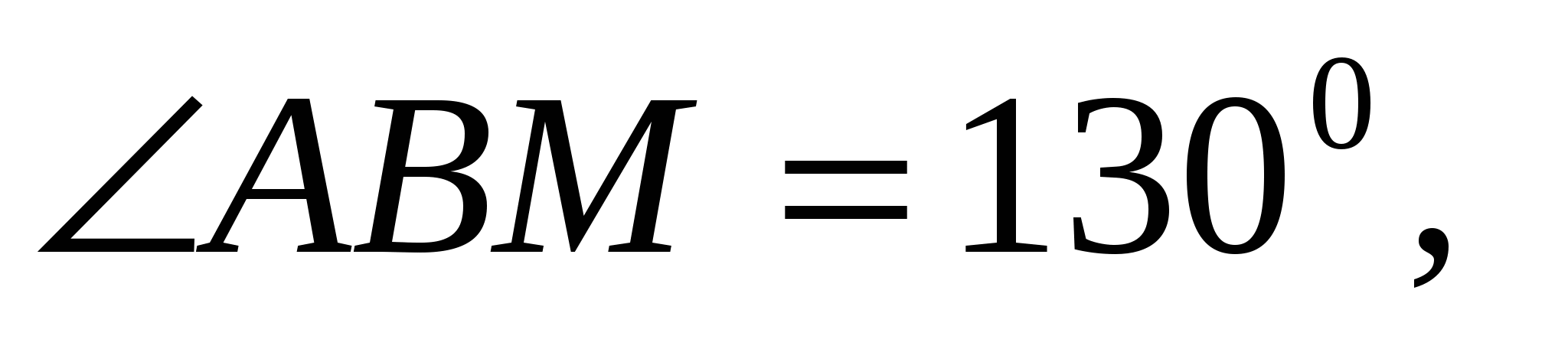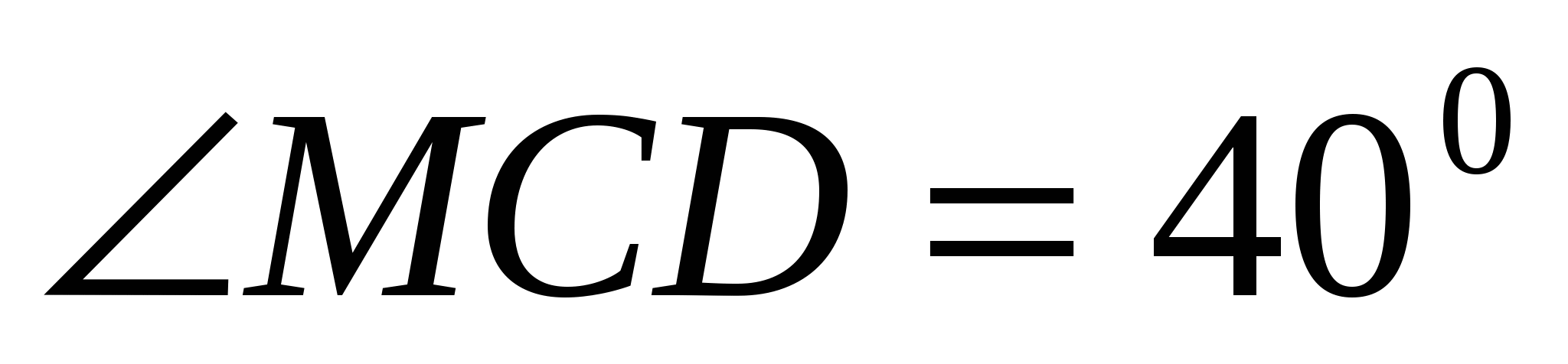. Найдите величину угла BMC.

Решение:

Через точку М проведем прямую МЕ, параллельную прямой АВ. Угол ЕМВ и угол АВМ односторонние при параллельных прямых АВ и МЕ, и секущей ВМ. Значит, их сумма равна 180° (по свойству параллельных прямых). Тогда угол ВМЕ равен 50°. Углы МCD и ЕМС равны как накрест лежащие при параллельных прямых МЕ и CD, и секущей МС. Значит, угол ЕМC равен 40°. Угол ВМС равен сумме углов ВМЕ и EМC. Значит, угол ВМС равен 90°.

Ответ: 90°.

№7. В круге проведены диаметр АВ и параллельные хорды АС и ВТ. Докажите, что СВ = ТА .

Доказательство: так как АВ – диаметр, то углы АСВ и ВТА – прямые. Углы САВ и ТВА равны как внутренние накрест лежащие при параллельных прямых. Треугольники АСВ и ВТА равны по гипотенузе и острому углу. Поэтому и СВ = ТА.

Вариант 7

№6. Угол А треугольника АВС равен 64⁰. Найдите меньший из углов между биссектрисами углов В и С.

Ответ: 58⁰ .

Решение: обозначим за ВК и СМ биссектрисы треугольника АВС, а за О – точку пересечения биссектрис. Тогда искомый угол МОВ будет равен сумме углов ОВС и ОСВ, то есть полусумме углов В и С треугольника АВС. Так как сумма углов треугольника равна 180⁰, то искомый угол МОВ равен (180⁰ – 64⁰)/2= 58⁰ .

№7. ABCD — параллелограмм. На сторонах AB, BC, CD, DA отмечены соответственно точки P, K, M и N так, что KC = AN , BP = MD. Докажите, что четырехугольник PKMN – параллелограмм.

Доказательство.

KC = AN, значит, BK = ND. PB = DM, значит, АР = MD. Треугольники ВРК и DMN равны по двум сторонам и углу между ними, т.к. ВК = DN, ВР = DM, ∠B =∠D (по свойству параллелограмма). Значит, стороны РК и MN равны. Также, треугольники APN и KCM равны по двум сторонам и углу между ними т.к. АР = MD., KC = AN, ∠A =∠C (по свойству параллелограмма). Значит, стороны РN и MК равны.

Таким образом, в четырехугольнике PKMN противоположные стороны равны.

Такой четырехугольник, по признаку параллелограмма – параллелограмм.

Вариант 8

№6. KA и KB — хорды окружности с центром в точке O, ∠AKB = 45°. Найдите длину хорды AB, если радиус окружности равен 4.

Решение:

1.∠AOB = 2∠AKB = 90° по свойству вписанного угла.

2. В треугольнике AOB: ∠O = 90°, AO = OB, AB = AO 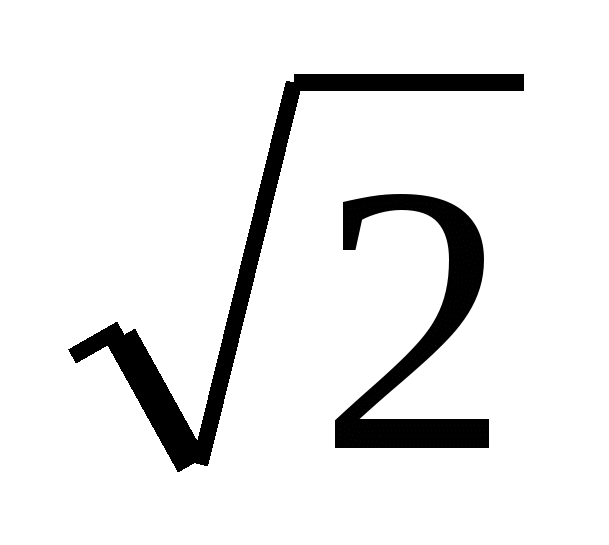= 4 .

Ответ: AB = 4 .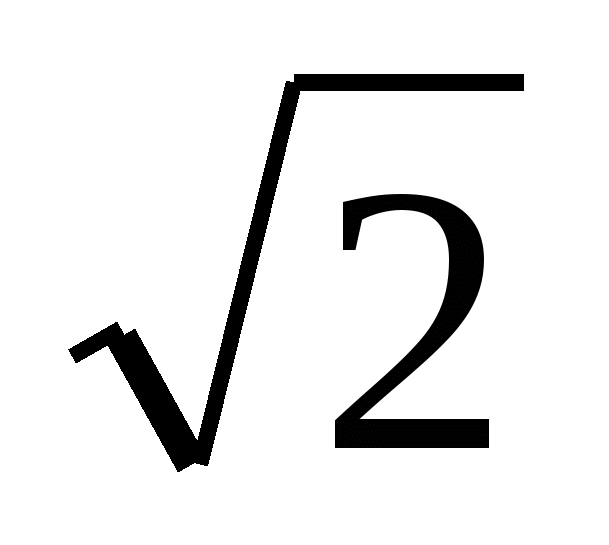

№7. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

Доказательство.

Треугольники BEC и AED равны по трём сторонам. Значит, углы CBE и DAE равны. Так как их сумма равна 180°, то углы равны 90°. Такой параллелограмм — прямоугольник.

ЛИТЕРАТУРА И ССЫЛКИ

1. Демонстрационный вариант (МА-9_ДЕМО2013_techno.pdf) http://fipi.ru/, 2013

2. http://ege.yandex.ru/mathematics-gia, 2013

3. Пробный ГИА С-Петербург. 2 варианта с ответами и критери ями .http://alexlarin.net/ege/2013/gia_160413.html, 2013

4. Пробный ГИА С-Петербург — 2 варианта с ответами и крит ериями http://alexlarin.net/ege/2013/gia_spb.html, 2013

5. 4 тренировочных варианта  ГИА-9 (Иркутск) с ответами и критериями http://alexlarin.net/ege/2013/gia_irk.html, 2013