VII ВСЕРОССИЙСКИЙ КОНКУРС
ПРОФЕССИОНАЛЬНОГО МАСТЕРСТВА ПЕДАГОГОВ
«МОЙ ЛУЧШИЙ УРОК»
естественно-научное направление
Муниципальное бюджетное общеобразовательное учреждение муниципального образования город Краснодар
средняя общеобразовательная школа № 71
ТЕОРЕМА
ПИФАГОРА
урок — путешествие
Автор:
Цеповяз Людмила Иосифовна,
учитель математики.
Предмет: геометрия ( естественно — научное направление)
Класс: 8 «Е»
Характеристика класса:
В 8«Е» классе обучаются 15 девочек и 14 мальчиков.
7 класс закончили без троек 15 учеников, с отличием — 1 человек.
Неуспевающих в классе по итогам учебного года нет.
Все учащиеся из благополучных семей, родители проявляют интерес к процессу воспитания и обучения.
Интересы детей разносторонние. Многие учащиеся занимаются спором, посещают кружки, занимаются музыкой, хореографией, активно участвуют в классных и школьных мероприятиях, олимпиадах .
В классе действует самоуправление, которое позволяет воспитывать у учащихся чувство ответственности, а также формировать личный опыт самореализации.
Тема: « Теорема Пифагора».
Программа и учебник по геометрии.
-
Программы для общеобразовательных учреждений. геометрия. 5- 9 классы/ Под редакцией Т.А. Бурмистрова. – М.: Просвещение , 2009.
-
Геометрия 7-9 класс под редакцией Л.С. Атанасян и др.-М : Просвещение 2009.
Количество часов в неделю по геометрии – 2, в году – 68.
Цель: Познакомить учащихся с теоремой Пифагора и ее доказательствами, используя
метапредметные связи, научить применять полученные знания на практике.
Задачи:
-
Формировать навык применения теоремы Пифагора при решении задач;
-
Расширить познания учащихся о жизни великого математика;
-
Создать особый эмоциональный настрой, способствующий развитию познавательных способностей учащихся;
-
Развивать информационную культуру учащихся.
Форма урока: урок – путешествие, рассчитанный на 2 академических часа.
Оформление: книжная выставка – « Выдающиеся учёные Древнего мира», портрет
Пифагора;
Оборудование: интерактивная доска, компьютер с программным обеспечением
Windows XP, чертежи для доказательства теоремы, таблицы «Пифагоровы тройки
чисел», презентация к уроку.
Рекомендации по проведению:
Проведению урока предшествовала подготовительная работа:
учащиеся подготовили исторические справки о жизни Пифагора, пифагорейской школе, о различных способах доказательства теоремы Пифагора (готовились все дети, задания были даны с учетом индивидуальных возможностей, проведены консультации учителем).
Ход урока
-
Организационный момент. Постановка целей урока
Слайд №1. (урок — путешествие Теорема Пифагора)
Слайд №2. (Эпиграф к уроку)
Пребудет вечной истина, как скоро
Все познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
А.Шамиссо
Слайд №3 (карта путешествия).
Вступительное слово учителя. Сегодня у нас урок – путешествие. На этом уроке вы познакомитесь с великим математиком мировой истории – Пифагором и его замечательной теоремой, научитесь решать задачи с ее помощью.
Маршрут путешествия: 1. Остров Самос в Эгейском море — родина Пифагора). 2. Река «Любознательных». 3. Остров «Треугольника».4. Гора «Знаний». 5. Бухта «Афоризмов»
Слайд №4
Учитель: Отправляемся в путешествие, и первая остановка — остров Самос, расположенный в Эгейском море. Перед вами карта Древнего мира с пунктами назначения нашего путешествия, найдите и покажите остров Самос.
Мы узнаем, чем интересен этот остров и какие «математические события» там происходили.
Слайд №5.
Вам было дано задание подготовить историческую справку о жизни Пифагора, о пифагорейской школе. Давайте послушаем сообщения ребят «О жизни и деятельности Пифагора».
Во время выступления учащихся идет показ слайдов №№ 6- 8
Слайд №9
Учитель: Молодцы, вы справились с заданиями, и мы продолжаем путешествие. Наш путь лежит дальше по реке «Любознательных», где вы познакомитесь с теоремой Пифагора и ее частными случаями. Что вы слышали о теореме Пифагора?
Ученики: Пифагоровы штаны во все стороны равны.
Учитель: Действительно, такое выражение существует, это шуточная формулировка теоремы. Такие стишки придумывали учащиеся средних веков и рисовали шаржи.
В настоящее время ученые утверждают, что эта теорема была известна до Пифагора, но доказана именно этим математиком. Давайте послушаем сообщения, подготовленные ребятами.
(Во время выступления учащихся идет показ слайдов №№ 10-14.
Слайд №15
Учитель: Молодцы, вы справились с заданиями. И мы продолжаем путешествие.
II. Повторение ранее изученного
Учитель: Ребята, я предлагаю вам отправиться по следам Пифагора на остров
«Треугольников».
Беседа с учащимися. Для начала давайте с вами ответим на некоторые вопросы, которые пригодятся нам для доказательства теоремы.
Слайд №16 (На экране появляются вопросы)
-
Какой треугольник называют прямоугольным?
-
Как называют его стороны?
-
Какие свойства прямоугольного треугольника вы знаете?
-
Как найти площадь прямоугольного треугольника?
Учитель: (Обобщает ответы учащихся). Пользуясь свойствами прямоугольных треугольников и свойствами площадей многоугольников, мы установим теперь соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы сегодня докажем, называется теоремой Пифагора. Она является важнейшей теоремой геометрии. “Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением,” — говорил Иоганн Кеплер Слайд .№ 17
Учитель: Вспомните, какова цель нашего урока. (Изучить теорему Пифагора, научиться решать задачи с использованием этой теоремы).
Запишем в тетрадях тему урока : «Теорема Пифагора».
Учитель: Успешно доказать теорему Пифагора нам поможет решение следующих
задач. Слайд № 18
Задача 1. Вычислите площадь треугольника АВС
Слайд №19
Задача 2. Найдите угол β
Слайд №20
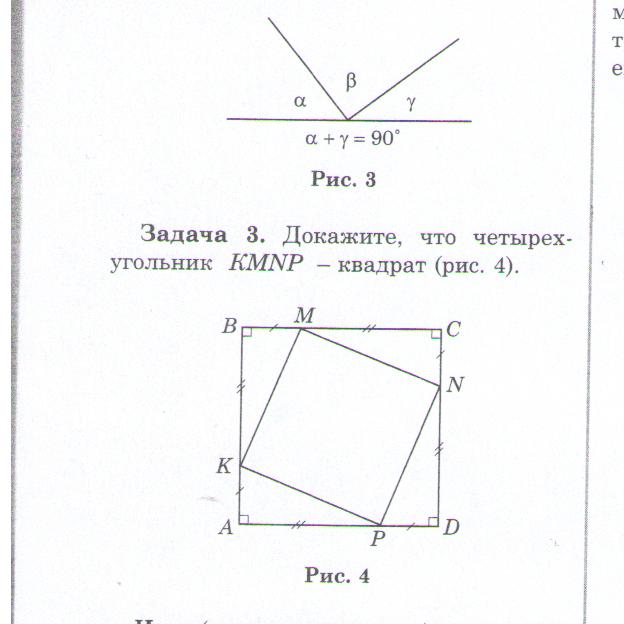
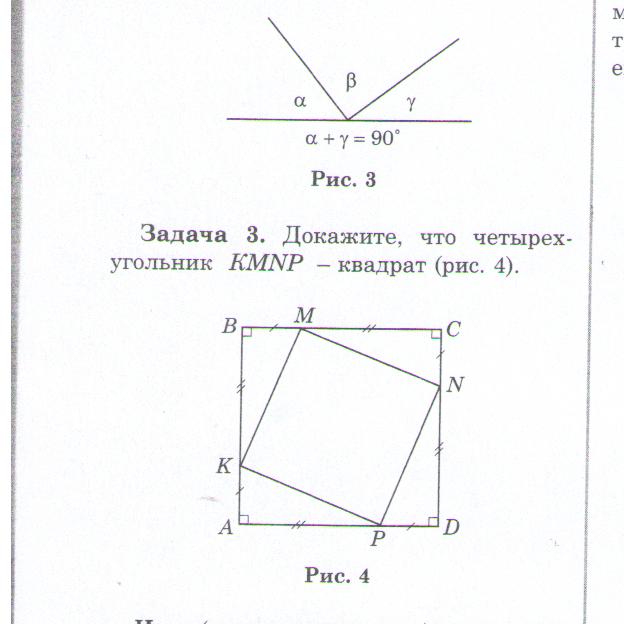
Задача 3.
Докажите, что четырёхугольник КМNP – квадрат
Учитель: Какие знания помогли вам при решении задач?
Учащиеся: Решить задачи нам помогло знание градусной меры развернутого угла,
использование формулы площади прямоугольного треугольника и применение
признака равенства прямоугольных треугольников по двум катетам.
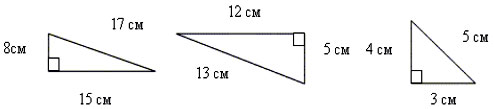
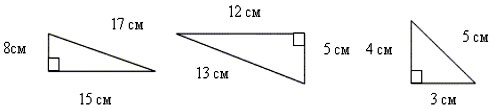
Учитель: Решим следующие задачи. Слайд №21
Учитель: Давайте на основе данных рисунков заполним соответствующую таблицу. В этой таблице нам надо записать квадраты длин катетов и квадрат длины гипотенузы для каждого из данных треугольников. У нас 3 треугольника, соответственно 3 строки таблицы нужно заполнить.
Дети выходят к доске и заполняют таблицу (на слайде №
| a 2 | b 2 | c 2 | |
| 1 треугольник | 64 | 225 | 289 |
| 2 треугольник | 144 | 25 | 169 |
| 3 треугольник | 16 | 9 | 25 |
21 появляется таблица с правильными ответами).
Учитель: Внимательно рассмотрите полученные значения в таблице? Какую
закономерность вы наблюдаете? (Сумма значений в первых двух столбцах равна
значению в третьем). Правильно! Эту закономерность заметил и Пифагор и доказал
одну из самых важных теорем геометрии.
III. Изучение нового материала.
Учитель: Наш путь лежит на Гору «Знаний». Слайд №22. Давайте прочитаем
формулировку теоремы в учебнике на стр.130 п. 54. Теорема: Квадрат гипотенузы
равен сумме квадратов катетов. «Теорема Пифагора» — теорема, которая отражает
связь между катетами и гипотенузой в прямоугольном треугольнике.
Знакомство с теоремой Пифагора. Доказательство проводит учитель. Слайд № 23.
Учитель: Что дано в условии теоремы?
Ученики: Прямоугольный треугольник, длины сторон прямоугольника (а,b,с).
Учитель: Что требуется доказать?
Ученики: Квадрат гипотенузы равен сумме квадратов катетов.
Учитель: Выполните в тетрадях чертёж, запишите условие теоремы.
Учитель: Вычисление площадей фигур уже помогало нам при доказательстве теорем. Для этого вспомним, с чего начинается доказательство теорем о площадях фигур. По аналогии с доказательствами достроим прямоугольный треугольник до квадрата (на экране треугольник достраивается до квадрата, появляются этапы доказательства теоремы).
Учитель: Сформулируйте вывод. (В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов). Ученики записывают доказательство теоремы в тетради.
Учитель: Эта теорема широко использовалась землемерами Древнего Египта. Для
построения прямого угла бечевку делили с помощью узлов на 12 равных частей. При
этом получали прямоугольный треугольник со сторонами 3, 4 и 5 единиц. Его назвали
египетским треугольником и использовали для построения прямых углов без
применения специальных измерительных приборов. Слайд № 24
IV. Закрепление изученного материала.
Учитель: Сегодня мы говорили о том, что Пифагор был разносторонней личностью. Он занимался и медициной, и математикой, был выдающимся спортсменом. А еще Пифагор был философом. Многие его афоризмы и сегодня актуальны для нас. С ними мы познакомимся в Бухте «Афоризмов».
Слайд № 25 Применение знаний по изученному материалу. Самостоятельная
работа с использованием интерактивной системы голосования.
Выполните несколько заданий. К каждому из них даны разные варианты ответов. Рядом записаны фрагменты афоризмов Пифагора. Ваша задача – решив задания, составить из полученных фрагментов высказывание математика.
Задачи Слайд № 26
№1. Катеты прямоугольного треугольника равны 3 и 4 см. Вычислите его гипотенузу.
№2. Диагональ прямоугольника ABCD — 10 см. Сторона АВ = 8 см. Вычислите сторону ВС.
Слайд № 27
№1. Вычислите катет прямоугольного треугольника, если другой катет равен 8, а гипотенуза 10 см.
№2. Стороны прямоугольника равны 12 см и 5 см. Вычислите длину диагонали.
Слайд № 28 №1.Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см.
№2. Найти боковую сторону равнобедренного треугольника, если основание равно 8 см, а высота, опущенная на основание 3 см
Учитель: Вы хорошо поработали. Я думаю, что эти афоризмы не раз пригодятся вам в жизни. Чтобы закрепить полученные на уроке знания, решим несколько задач. При решении используйте алгоритм применения теоремы Пифагора.
Слайд № 29
Задача 1. Дано: АВСД – ромб. АС =24 см, ВД=10см. Найти: СД.
Задача 2. Дано: АВСД — прямоугольник. АС =10 см, ВС=6см . Найти: АВ.
Задача 3. Дано: АВС — равнобедренный треугольник. АВ=ВС=5 см ВД – высота ВД= 4 см . Найти: АС.
Задача 4. Дано: АВС прямоугольный треугольник. АВ =12 см, СА=9см. Найти: ВС.
Слайд № 30
V. Подведение итогов урока. Рефлексия
Учитель: Подведем итог нашего путешествия.1.С какой теоремой вы сегодня познакомились? 2.В чём заключается теорема Пифагора? 3.Какую закономерность она подтверждает? 4. Что нового вы узнали о Пифагоре — математике и философе?
Слайд №31 (На экране – высказывание Д. Пойя «Где есть желание, найдется путь».
Я хотела бы завершить наш урок словами знаменитого математика Джорджа Пойя.
Благодаря нашему стремлению к новым знаниям, мы смогли сегодня проделать тот
же путь, который прошел много веков назад великий древнегреческий математик
Пифагор.
-
Домашнее задание: П. 54, № 483(а, б), 486 (а, б). Творческое задание:
самостоятельно посетить остров любознательных и разобрать другие способы доказательства теоремы Пифагора. Познакомить нас с новыми способами на следующем уроке. Слайд №32
Слайд №33 (Спасибо за урок)
Список использованной литературы:
-
Энциклопедия для детей Т.11. Математика М. Аванта+, 2001г.
-
Школьная энциклопедия. Математика. Москва: Научное издательство «Большая Российская энциклопедия», 1996 г.
Список использованных Интернет-ресурсов:
-
http://festival.1september.ru/articles/514101/
-
http://pokrovskayashkola.narod.ru/pifagor.htm
-
http://900igr.net/fotografii/geometrija/Teorema-Pifagora-geometrija/021-K-teoreme-Pifagora-ego-ucheniki-sostavljali-stishki-vrode.html
-
http://rudocs.exdat.com/docs/index-590.html
-
http://napolyah.livejournal.com/45028.html
Материалы к уроку
Ученик 1: Пифагор родился в 576 г. до н.э. на греческом острове Самос, расположенном в Эгейском море. По совету Фалеса 22 года Пифагор набирался мудрости в Египте. Во время завоевательных походов на Египет войска полководца Камбиза взяли Пифагора в плен и продали в рабство. Так он оказался в Вавилоне, где прожил более 10 лет. Там он изучал древнюю культуру и достижения науки разных стран. После возвращения домой он поселился в Италии, а затем в Сицилии. Пифагор–это не имя, а прозвище, данное ему за то, что он высказывал истину так же постоянно, как дельфийский аракул (“Пифагор” значит “убеждающий речью”.) Слайд№5
В результате первой же прочитанной лекции Пифагор приобрёл 2000 учеников, которые не вернулись домой, а вместе со своими жёнами и детьми образовали огромную школу и создали государство, названное “Великая Греция”. Слайд № 6-7
Так Пифагор организовал свой пифагорейский орден и школу философов и математиков. Туда принимали с большими церемониями и после долгих испытаний. Здесь существовал декрет, по которому авторство всех математических работ приписывалось самому Пифагору. В школе была очень серьезная дисциплина. Главным безоговорочным аргументом в научных спорах были слова “сам сказал”. После этого дискуссии прекращались. Пифагор и его ученики были трудолюбивы и аскетичны. Вот их заповеди: Слайд №8
-
делать то, что впоследствии не огорчит тебя и не принудит раскаиваться;
-
не делай никогда того, чего не знаешь, но научись всему, что следует знать;
-
не пренебрегай здоровьем своего тела;
-
приучайся жить просто и без роскоши.
Ученик 2: В пифагорейской школе много внимания уделялось музыке, живописи, физическому развитию, здоровью. Известно, что Пифагор четыре раза был Олимпийским чемпионом. Этого крепкого юношу с упрямой шеей и коротким носом, настоящего драчуна судьи одной из первых в истории Олимпиады не хотели допускать к соревнованиям по кулачному бою, укоряя его маленьким ростом. Он пробился и победил всех противников. Пифагорейцами было сделано много открытий в каждом из этих направлений науки того времени. Одно из самых важных – это известная теорема Пифагора. Долгое время считалось, что до Пифагора эта теорема не была известна и поэтому она получила такое название. Однако в настоящее время установлено, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора. Заслуга Пифагора заключается в том, что он впервые доказал её. Сохранилась легенда, которая гласит, что, доказав свою знаменитую теорему, Пифагор принёс богам в жертву быка, а по другим источникам 100 быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он “запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как мы”. Пифагор питался только мёдом, хлебом, овощами и изредка рыбой. В связи с этим более правдоподобной можно считать следующую запись: “…и даже когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принёс в жертву быка, сделанного из пшеничного теста”. Пифагор был убит в уличной схватке во время народного восстания. После смерти его ученики окружили имя своего учителя множеством легенд, так что правду о Пифагоре установить невозможно.
Ученик 3: Историческая справка «О теореме Пифагора»: (подготовлена
учащимися) Слайд №№ 10-14
Теорема о связи между длинами сторон прямоугольного треугольника не была открыта Пифагором. Она была известна еще до него.
Её знали в Китае, Вавилоне, Египте. Вернее, не ее, а частные случаи. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, другие же отказывают ему и в этой заслуге. Зато не найти, пожалуй, никакой другой теоремы, имеющей столько всевозможных названий. Во Франции и Германии в Средневековье теорему Пифагора называли ,,мостом ослов” или ,,бегством убогих”, потому что перед экзаменом, содержащим вопросы по этой теме, начинался массовый отток нерадивых студентов. У математиков арабского Востока эта теорема называлась ,,теорема невесты”. Дело в том, что в некоторых списках ,,Начал” Евклида эта теорема называлась ,,теорема нимфы” за сходство чертежа с пчелкой, бабочкой (по- гречески –нимфы). Но словом ,,нимфа” греки называли еще и некоторых богинь, а также молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимание на чертеж, перевел слово ,,нимфа” как ,,невеста”, а не ,,бабочка”. Так появилось ласковое название знаменитой теоремы — ,,теорема невесты”.
Рассказывают, что когда Пифагор доказал свою знаменитую теорему, он отблагодарил богов, принеся в жертву сто быков. И поэтому её ещё называют теоремой «100 быков».
В настоящее время известно около 200 доказательств теоремы Пифагора
Задания
| №2. Диагональ прямоугольника ABCD — 10 см. Сторона АВ = 8 см. Вычислите сторону ВС. | |
|
|
|
|
|
|
| 6 – не бегай за счастьем | 6 – оно всегда находится в тебе самом |
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
Карточка для B – II.
| №2. Стороны прямоугольника равны 12 см и 5 см. Вычислите длину диагонали. | |
|
|
|
| 4 – формулы | 13 – управляют миром |
|
|
|
Ответ: Числа управляют миром.
Карточки для B – III
| №2. Найти боковую сторону равнобедренного треугольника, если основание равно 8см, а высота, опущенная на основание — 3см. | |
|
|
|
| 8 – либо молчи | 5 – либо говори то, что ценнее молчания |
| 64 – хочешь-молчи | 6 – или говори о том, что интересно всем |
Ответ: Либо молчи, либо говори то, что ценнее молчания.
Проверка результатов (чтение афоризмов) (каждая группа предлагает свои ответы):
1.Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
2.Ответ: Числа управляют миром.
3.Ответ: Либо молчи, либо говори то, что ценнее молчания.